基于流量脉动系数的齿轮泵齿廓的主动设计及特性分析

(1.南京工程学院 机械工程学院， 江苏 南京 211167； 2.中南大学 机电工程学院， 湖南 长沙 410083；3.厦门理工学院 机械与汽车工程学院， 福建 厦门 361024)

引言

齿轮泵具有体积小、重量轻、转速范围大、自吸性能好等优点，被广泛应用于机床、冶金、矿山、航天等机械产品的液压系统中。齿轮泵输出流量脉动大的缺陷(流量脉动高达15%～27%)限制了齿轮泵的使用范围[1-3]。目前，降低齿轮泵流量脉动的方法主要有[4]：采用级联齿轮泵，通过二级并联齿轮泵的输出流量进行叠加，可使齿轮泵的总体输出流量脉动下降，三级以上的并联齿轮泵可使流量脉动下降的更多，但制造和装配的难度更大；采用平衡式复合齿轮泵，由于平衡式复合齿轮泵内部各齿轮的相位相错， 使得其流量脉动有所下降；采用非对称渐开线齿轮泵，采用非对称渐开线齿形齿轮泵，其瞬时流量的脉动频率增高，振幅自然有所下降。另外，还有通过增设滤波器、采用双模数齿轮、采用新型结构等降低齿轮泵的流量脉动，但效果均不明显[1,5]。综上所述，有些降低齿轮泵流量脉动的方法效果不明显，而有些方法虽然降低了齿轮泵的流量脉动，但是其结构较为复杂，使得齿轮泵的加工成本增加。

利用主动设计方法，可以在设计阶段对齿面传动性能进行直接、有效的控制，以此获得齿廓曲线方程或基本产形齿条方程。近年来，基于功能需求或预定啮合性能或给定运动规律的齿廓主动设计已经成为齿轮领域的研究热点。YE等[6]以传动性能指标最优为设计条件，建立了基本产形齿条的齿廓方程，并以线接触斜齿轮为例，研究了设计参数对共轭齿廓曲率半径、齿面润滑油膜最小厚度的影响。LIN等[7]引入啮合角函数的概念，建立了描述平面齿轮共轭齿廓几何特征的通用数学模型，并设计了圆形及非圆齿轮齿廓。田兴等[8]采用少齿数的非对称渐开线直齿轮主动设计方法，计算了不同齿数齿轮副的参数以及齿轮副啮合所能达到的最大重合度。王建等[9]提出了一种基于压力角函数的高重合度齿轮的主动设计方法。陈广艳等[10]根据齿面印痕的偏移，识别相应的当量错位，并将其反馈到齿面设计中，提出了弧齿锥齿轮的主动设计方法。

本研究将主动设计引入到齿轮泵设计领域，以齿轮泵的流量脉动系数作为设计变量，建立了基于流量脉动系数的齿廓齿廓的数学模型，给出了齿廓约束限制条件，通过预设定齿轮泵的流量脉动系数，可以实现对齿轮齿廓进行直接、有效的控制。

1 基于流量脉动系数的齿廓主动设计的数学模型

1.1 基于极距和压力角函数的齿轮齿廓的数学描述

如图1所示，坐标系∑1(x1,o1,y1)与主动齿轮相固连，坐标系∑2(O2,x2,y2)与从动齿轮相固联，∑0(O0,x0,y0)为固定坐标系，定义极距λ表示齿轮啮合点P1到节点P的距离，α为压力角函数，其可表示为转角φ的一次函数，即：

(1)

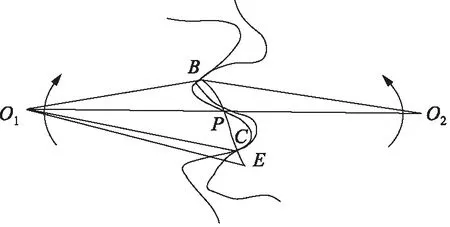
其中，C0和C1分别为压力角函数的系数，C0的取值范围为0

图1 基于极距和压力角函数的齿轮啮合坐标系

若采用λd表示当啮合点位于主动齿轮的齿根圆和节圆之间时的极距，采用λa表示当啮合点位于主动齿轮的齿顶圆和节圆之间时的极距，由文献[9]可知，下式成立:

(2)

主从动齿轮的齿廓方程可表示为[9]:

(3)

(4)

其中，u表示齿轮传动比，r1表示主动齿轮的节圆半径，E和F可表示为：

E=sin(C0+C1φ)-sinC0

F=sin(C0-C1φ)-sinC0

当φ取正值时，式(3)和式(4)分别代表从动齿轮齿根和主动齿轮齿顶部分的方程，反之，当φ取负值时，式(3)和式(4)分别代表从动齿轮齿顶和主动齿轮齿根部分的方程。

1.2 齿轮泵流量脉动系数的数学模型

流量脉动系数的值越大，表示出口处流量脉动越严重，反之越平缓。流量脉动系数δ可表示为：

(5)

式中， (Qsh)max， (Qsh)min分别表示瞬时流量的最大值以及最小值。

图2为齿轮泵的工作原理图，由文献[11]可知，主从动齿轮包围压油腔的齿面所扫过的容积dV1和dV2可分别表示为：

(6)

(7)

其中，re1，rc1分别表示主动齿轮的齿顶圆半径和啮合半径，re2和rc2分别表示从动齿轮的齿顶圆半径和啮合半径，B为齿轮齿宽。

在dt时间内，齿轮泵排出油液的体积为主从动齿轮扫过的容积之和，即dV1=dV1+dV2，则瞬时流量可表示为：

(8)

根据齿轮泵中主从动齿轮的齿数、模数和压力角分别相等，式(8)可进一步简化为：

(9)

其中，r表示两齿轮的节圆半径，λ表示极距，是φ的函数。

图2 齿轮泵工作示意图

由式(9)可知，齿轮泵的瞬时流量随着极距λ或转角φ呈抛物线规律变化。当啮合点与节点重合时，即当λ=0时，瞬时流量最大，其最大值可表示：

(10)

图3为齿轮啮合示意图，其中B点和E点分别表示啮合起始点和脱离啮合点，两齿轮在B点进入啮合并开始排油，到C点时排油结束，而在C点和E点之间的过程，第1对轮齿不参与排油，此为1个周期，以后各对轮齿都重复上述周期。根据文献[11]，外啮合齿轮泵瞬时流量的最小值发生在齿轮刚进入啮合开始排油的时刻，由式(3)和式(9)可知，其最小值可表示为：

(11)

其中，φB为B点所对应的φ角值。

图3 齿轮啮合示意图

将式(10)、式(11)带入式(5)可得，齿轮泵的流量脉动系数可表示为：

1.3 基于流量脉动系数的齿廓数学描述

将式(12)进一步变换并代入式(3)和式(4)，齿廓方程可表示为：

φ≥0

φ≤0

(13)

φ≥0

φ≤0

(14)

1.4 齿廓约束限制条件

齿廓的形成与压力角函数系数的C1和C0的取值有很大关系，若C1和C0的取值不当则齿廓会出现尖点或交叉，因此必须限制C1和C0的取值，以避免发生齿顶变尖和齿廓交叉。

图4为一个轮齿齿顶部分(分度圆和齿顶圆之间)的两侧齿廓，虚线为轮齿中心线，由图4可知，当齿廓k0与中心线相交时，齿顶圆上的齿宽为0，即齿顶变尖。此时的流量脉动系数即为最小值δmin。

图4 齿廓曲线示意图

由图4可知，齿顶圆的直角坐标方程为：

(15)

联立式(3)和式(15)，可得C1和C0的关系式为：

Ecos[C0+(1+C1)φ]=C1(cosφ+sinφ) (16)

其中，φ为齿轮转角，其值为φ=90/z。

根据式(16)，对C1赋值，可求出C0的值。将C0和C1分别带入式(12)，可得δmin为：

(17)

因此，要避免齿顶变尖，预先给定的流量脉动系数的限制条件为δ>δmin，即:

(18)

齿轮1上点的曲率为:

(19)

由式(19)可知，当曲率为正时，齿廓为凸齿廓，因此齿廓出现尖点的条件为曲率半径为0，即:

(20)

即通过式(18)和式(20)即可确定压力角函数系数C0和C1的取值范围。同理可知，式(18)和式(20)对齿轮2同样成立。

2 设计实例

图5 流量脉动系数曲线

C0π/6π/7π/8π/9C1[0.01,0.7)[0.08,1.3)[0.1,1.6)[0.2,2)

根据图5，选择C0=π/6，π/7，π/8的曲线，预先给定齿轮泵的流量脉动系数分别为δ=10%，11%，12%，则对应的C1的值分别为0.18，0.4，1.09，将其带入式(13)和式(14)，可分别得到主动齿轮和从动齿轮齿廓的方程。图6为绘制的3种流量脉动系数下的齿轮齿廓曲线，为了便于比较，图6还给出了相同参数(除压力角不同外，其压力角为α=20°)的渐开线齿轮的齿廓曲线。

由图6可知：在分度圆和齿顶圆之间，随着流量脉动系数的增大，齿轮的轮齿宽度逐渐增大，且均小于渐开线齿轮轮齿的齿宽；在分度圆和齿根圆之间，随着流量脉动系数的增大，齿轮的轮齿宽度逐渐减小，且均大于渐开线齿轮轮齿的齿宽，有利于提高齿轮的齿根弯曲强度。

图6 齿廓曲线对比

3 齿轮泵结构设计及特性分析

3.1 结构设计

本研究设计的齿轮泵属于低压齿轮泵，故齿轮泵采用三片式结构。基于流量脉动系数的齿轮泵的参数为：C0=π/6，C1=0.18，流量脉动系数δ=10%。如图7所示的整体结构图，主要由泵体、齿轮、前端盖、轴承、骨架油封等零部件组成，齿轮与轴之间采用平键连接。泵体、前、后端盖材料为QT500-7球墨铸铁，齿轮材料为40Cr，轴材料为45钢，轴承为SF-1无油润滑轴承或滚针轴承。图8和图9分别为加工出的齿轮和装配好的齿轮泵。

1.前盖 2.定位销 3.密封圈 4.从动轮 5.滑动轴承 6.从动轴 7、8.平键 9.主动轴 10.滚动轴承 11.主动轮 12.壳体 13.后盖 图7 齿轮泵整体结构图

图8 加工出的齿轮

设计参数取值功率P/kW0.21额定转速n/r·min-11450额定压力F/MPa2.5传动比u1.0额定流量Q/L·min-14总效率η80%使用寿命/h5000齿宽B/mm8

图9 装配好的齿轮泵

3.2 特性分析

1) 瞬时流量

齿轮泵的瞬时流量可以从微观的角度反映出齿轮泵的吸油排油过程。将齿轮泵的结构参数代入式(11)和式(12)可得，齿轮泵瞬时流量的最大值和最小值分别为4.373 L/min和3.936 L/min。为了便于比较，本研究同样计算出了相同参数的渐开线齿轮泵的最大和最小瞬时流量，分别为4.373 L/min和3.964 L/min。与渐开线齿轮泵相比，所设计的齿轮泵的最小瞬时流量增加了6.6%，最大瞬时流量和渐开线齿轮泵相同，上述结果表明，所设计齿轮泵的瞬时流量波动幅度、啮合冲击和运转平稳性均优于渐开线齿轮泵。

2) 几何排量

齿轮转动1周，吸油和排油各1次，齿轮泵的排量可表示为：

q=zVn

(21)

其中，Vn表示1对轮齿在1次啮合过程中所排出液体的体积，可利用下式求得：

(22)

利用数值计算方法，可得齿轮泵的排量为：

(23)

将齿轮参数分别带入式(23)，可得所设计出齿轮泵的排量为2.759 mL/r。根据文献[12]，可计算出相同参数的渐开线齿轮泵的排量为2.733 mL/r。与渐开线齿轮泵相比，所设计齿轮泵的排量增加了0.9%。

3) 平均流量

平均流量表示排油量的平均值，可以从宏观的角度反映齿轮泵的吸排油过程，可表示为：

Qm=q·n

(24)

利用上式计算可得所设计齿轮泵和渐开线齿轮泵的平均流量分别为4 L/min和3.963 L/min。通过对比可知，所设计出的齿轮泵的平均流量比渐开线齿轮泵增加了0.9%。

4) 流量脉动系数

将齿轮泵瞬时流量的最大值和最小值分别代入式(5)，可计算得到所设计齿轮泵和渐开线齿轮泵的流量脉动系数分别为10%和15.5%。为了便于和理论结果进行比较，利用MATLAB软件，对齿轮泵的最大和最小瞬时流量、流量脉动系数在(0, 8 ms)内进行了仿真，如图10所示。表3同时给出了其具体数值。为了进行比较，本研究利用如图11所示的齿轮泵试验台在额定转速和额定压力下进行了测试，测试时间5 min，测试结果如表3所示。

a.本研究设计的齿轮泵 b.渐开线齿轮泵图10 仿真曲线

齿轮泵最大瞬时流量Qmax/L·min-1最小瞬时流量Qmin/L·min-1平均流量Q/L·min-1流量脉动系数δQ/%本研究设计的齿轮泵仿真值4.3733.9034.13810.5实验值4.2543.8394.0499.75渐开线齿轮泵仿真值4.3733.7084.04115.2实验值4.1563.6373.88912.5

图11 齿轮泵测试试验台

由表3可知：

(1) 从仿真结果来看，两齿轮泵最大瞬时流量相同，本研究所设计齿轮泵的最小瞬时流量比相同参数的渐开线齿轮泵增大了5.3%，平均流量增大了2.4%，流量脉动系数减小了29.6%；

(2) 从试验结果来看，本研究所设计的齿轮泵的最大瞬时流量、最小瞬时流量比渐开线齿轮泵分别增加了2.3%和5.3%，流量脉动系数减少了22%；

(3) 本研究所设计的齿轮泵的流量脉动系数的初始给定值为10%，仿真得出的数值为10.5%，试验测得的值为9.75%，均在误差允许的范围内，说明了本研究设计方法的正确性。

4 结论

传统的降低齿轮泵流量脉动的方法是以结构复杂为代价的，齿轮泵的结构和工艺在各类液压泵中结构最简单的优点近乎丧失。本研究从齿轮齿廓的设计入手，推导了采用极距和压力角函数描述的齿廓方程，以齿轮泵的流量脉动系数作为设计变量，建立了基于流量脉动系数的齿廓主动设计的数学模型。其优点是将齿轮泵的流量脉动系数作为一个给定值，即在设计的同时，就已经知道了流量脉动系数的大小。研究成果可为缓解齿轮泵的流量脉动提供理论依据和技术支持，并为齿轮泵的设计提供一个新的思路和更为广阔的研究空间。