汽车主动悬架H2/H∞多目标优化控制

段建民，黄小龙

(北京工业大学信息学部，北京 100124)

在1/4车辆模型中无法反映前后悬架之间的联动关系，而在半车悬架协同控制中，不仅期望反映行驶平顺性的垂直加速度和俯仰角加速度值小，又要求悬架的动行程只能在给定的行程内变化，同时要求车轮和路面间的动位移较小，这样车轮和路面具有良好的附着效果，然而这3个评价标准在客观上存在矛盾。为解决此问题，文献[1—2]针对两自由度车辆的悬架模型设计混合H2/H∞状态反馈控制器，该控制器只是针对1/4车，无法体现行驶平顺性和操纵稳定性的性能指标，尤其对路面剧烈变化的凸包，未做相关的性能约束。文献[3]提出混合H2/H∞输出反馈控制器，通过选取加权函数对悬架的频域性能指标进行整定，但性能指标改善不明显。针对上述问题，也有文献采用别的控制方法，但存在相应的不足，如：利用模糊PID控制车身加速度和悬架动挠度，对其他性能未做约束，鲁棒性能差；神经网络控制系统的学习过程较长，进而适应性和实时性较差；LQG控制很难选择合适的加权值，使其性能限制在范围内。

H∞控制方法能较好处理鲁棒稳定性的问题，但动态性能较差。H2控制方法能够得到优越的动态性能，但鲁棒稳定性较差。如果结合2种控制方法的优点，设计 H2/H∞混合控制器，使主动悬架系统不仅具有较大的鲁棒稳定性，而且满足一定的鲁棒性能要求。本文选择4自由度半车电液主动悬架作为控制对象，设计出一种基于LMI的H2/H∞多目标全状态反馈最优鲁棒控制器。该控制系统选择用H2范数表示平顺性指标，选择操纵稳定性指标H∞范数表示控制力、悬架行程约束和接地性。仿真结果表明该控制方案与被动悬架相比，在舒适性与操纵稳定性方面得到相应的改善。

1 运动方程

半车四自由度主动悬架模型的变量符号如图1所示，半车身质量和俯仰运动的转动惯量分别用m2，Iφ表示；前、后轮的非簧载质量分别用m1f和m1r表示；前悬架产生的弹性力和阻尼力分别用ksf和csf表示；后悬架产生的弹性力和阻尼力分别用ksr和csr表示；前、后轮胎产生的弹性力分别为ktf和ktr；车身绕y轴俯仰角为φ；前、后簧下质量位移分别用zuf和zur表示；前、后路面扰动位移输入分别用zrf和zrr表示；前、后悬架组件纵向距离到车身质心的距离分别由a和b表示；前、后悬架控制力分别用uf和ur表示。根据牛顿第二定律可获得半车悬架系统动态微分方程：

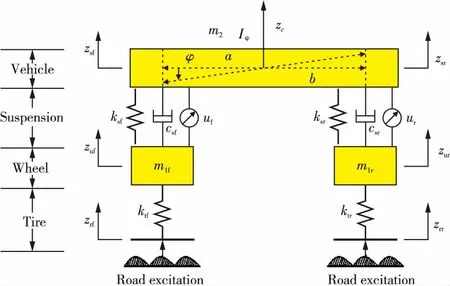
图1 半车四自由度主动悬架动力学模型

(1)

当俯仰角φ较小时，可以近似得到：

zsf(t)=zc(t)-aφ(t)

(2)

zsr(t)=zc(t)+bφ(t)

(3)

对式(1)-(3)变换，可以得到:

(4)

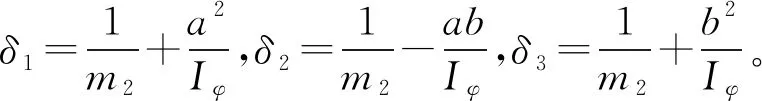
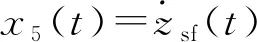
(5)

式中，x=[x1(t)x2(t)x3(t)x4(t)x5(t)x6(t)x7(t)x8(t)]T

u(t)=[uf(t)ur(t)]T

在半车主动悬架控制器设计中，需要考虑以下的性能要求。

(6)

2)悬架行程约束。悬架行程在安全的行程范围内满足式(7)不等式：

|zsf(t)-zuf(t)|≤zfmax
|zsr(t)-zur(t)|≤zrmax

(7)

式中，前、后悬架最大行程值分别用zfmax和zrmax表示。

3)接地性。实现操纵稳定性需满足式(8)不等式：

|ksf(zuf(t)-zrf(t))|≤Ff
|ksr(zur(t)-zrr(t))|≤Fr

(8)

式中，前、后轮胎的静载分别用Ff和Fr表示，其计算公式如下:

Fr(a+b)=m2ga+m1rg(a+b)

Ff+Fr=(m2+m1f+m1r)g

这里我们定义第二组控制输出

(9)

式(9)包含着对式(7)和式 (8)的性能约束，这时可以得到含外部扰动输入的半车主动悬架系统的状态空间方程式：

(10)

式中，

C2=

C∞=

广义被控主动悬架的状态方程描述如下：

(11)

式中，u为控制信号；ω为外部输入信号；z∞和z2为对应的H∞和H2指标被控输出，且有x∈Rn，u∈Rm，ω∈Rq，z∞∈Rr1，z2∈Rr2。

2 多目标优化控制算法设计

图2为主动悬架H2/H∞多目标状态反馈优化控制器设计框图。从图中可以看出，其核心设计问题为控制器控制律的算法设计，即通过设计相应的控制算法求解控制增益矩阵K，液压装置看成执行机构。

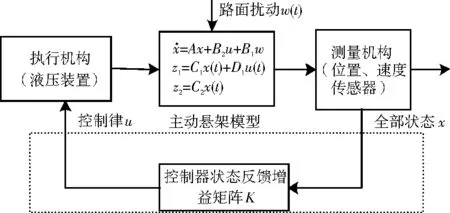
图2 控制系统结构图

设计一个全状态反馈控制器u=Kx， 由此相应的闭环系统描述为：

(12)

闭环系统(12)若满足以下性能指标：1)闭环系统是渐近稳定的，即闭环系统的全部极点必须位于S平面左半平面；2)给定标量γ1为正数，从外部扰动ω到z∞的闭环传递函数Tz∞ω的H∞范数不大于上界γ1，以确保闭环系统对由ω=△z∞进入的不确定性具有扰动抑制；3)从外部扰动ω到z2的闭环传递函数Tz2ω的H2范数尽可能小，以确保采取H2范数度量的系统有优越的性能。 则称为系统(11)的多目标H2/H∞的状态反馈控制器[5-6]。

定理1 对于广义线性时不变系统(11)以及标量γ1>0，γ2>0，存在一个状态反馈H2/H∞控制律，当且仅当存在对称正定矩阵X和Z，使得，

AX+B2W+(AX+B2W)T<0

tr(Z)<γ2

求解得到一个最优解X、W，则广义线性时不变系统(11)的状态反馈H2/H∞控制律为

u=WX-1x

3 半车全状态多目标最优H2/H∞控制仿真分析

为验证所提出基于LMI的H2/H∞多目标优化控制算法的效果，仿真工况根据《GB/T 4970-2009 汽车平顺性试验方法》要求，假设平整路面上有一个包块，作为路面扰动脉冲输入，路面的时域模型可表达为[7-8]

式中：zr(t)为路面垂向位移，m；h和l分别表示包块的高度和宽度，m；v0为恒定的车辆前进速度，m/s。在本次仿真中，v0为10 m/s，h=0.07 m，l=2 m，并假设前后轮路况一样，只是存在(a+b)/v0时间延时，即相差0.3 s。

表1为半车主动悬架的模型参数。

表1 车辆参数

根据车辆参数通过matlab计算得到γ1和γ2相关数据，由最小二乘法拟合得到曲线，如图3所示。从图中可以看出，系统的H2的范数和H∞的范数之间存在着一种反比例的关系，即γ2增大时，γ1减小。这说明了在实际设计当中，反映行驶平顺性的垂直加速度和俯仰角加速度值与悬架动行程、轮胎动位移和接地性始终存在矛盾，是不可兼得的。若γ1取的值过小，主动悬架的闭环系统动态性能优越，但行驶平顺性稍差[9]；若γ1取的值过大，主动悬架的闭环系统动态性能越差，但行驶平顺性能够提高。这就需要对γ1进行合理的折中，设计的控制器才能满足具体的工况要求。

图3 H2保性能指标值γ2和H∞扰动抑制度γ1之间的关系

CaseⅠ：γ1值选取方法[2]。从图3中可以看出，γ1值从2.5开始后，随着H∞的范数减小，H2的范数变化缓慢。这说明设计的控制器保证最好折中的γ1值在2.5 附近，以便实现系统鲁棒性能和时域性能的优势。本文选取γ1=2.5进行H2/H∞控制器的迭代求解，求出的全状态最优控制反馈增益矩阵为

CaseⅡ：为了形成对比验证，选取另外一个γ1值为11，求出的反馈增益矩阵如下。该工况下，行驶平顺性得到极大提高，但闭环系统动态性能变得很糟糕。

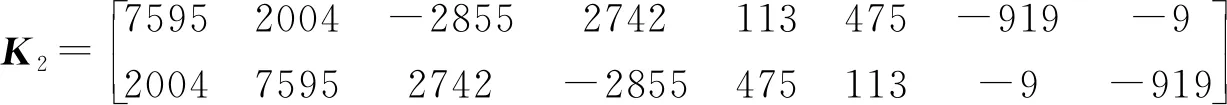
为了研究该方法的可行性，将与半车被动悬架进行对比。在时域内比较垂直加速度、俯仰角加速度、悬架动行程、控制执行力和轮胎动位移动态特性。由表2可知：CaseⅠ主动悬架与被动悬架相比车身加速度、俯仰角加速度分别降低了59.1%，84.21%；CaseⅡ主动悬架与被动悬架相比车身加速度、俯仰角加速度分别降低了51.29%，75.75%。图4和图5是车身垂直加速度和俯仰角加速度的时域响应图。通过与被动悬架比较，该方法可以同时降低垂直加速度和俯仰角加速度，实现扰动抑制，改善车辆行驶的舒适性，但是CaseⅡ主动悬架在牺牲 H∞性能基础上，得到更好的H2性能。

表2 性能指标均方根的比较

由图6和图7 前、后悬架动行程的时域响应图可知：CaseⅠ悬架的行程能够约束在最大行程之内，避免冲击限位装置，不仅获得较好的平顺性，而且安全性得到保障，使安全性与平顺性达到最好的折中状态；CaseⅡ悬架的动行程收敛速度没有被动悬架快，虽然平顺性改善，但以动挠度恶化为代价。图8和图9是主动悬架主动控制力的时域响应图。执行机构输出控制力限制在设计范围为(-2 500 N，2 500 N)，避免液压装置输出饱和，但是CaseⅡ悬架的输出控制力动态特性劣于CaseⅠ悬架，出现振荡，然后稳定。图10和图11是主动悬架前轮和后轮动位移的时域响应图。在前后轮经过凸包时，该动载和静载之比小于1，保证轮胎的接地性，实现车辆行驶的安全性，但CaseⅠ悬架的操纵稳定性优势比较明显。

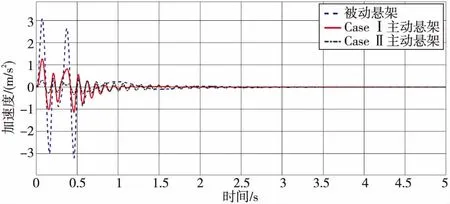
图4 车身加速度

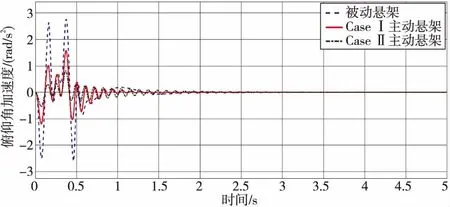
图5 俯仰角加速度

图6 主被动前悬架行程

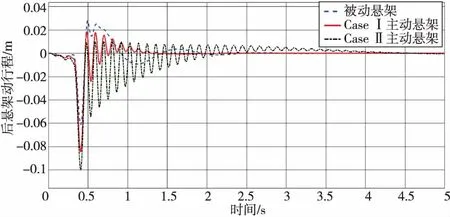
图7 主被动后悬架行程

图8 CaseⅠ前后悬架主动控制力对比

图9 CaseⅡ前后悬架主动控制力对比

图10 CaseⅠ主动悬架轮胎动位移

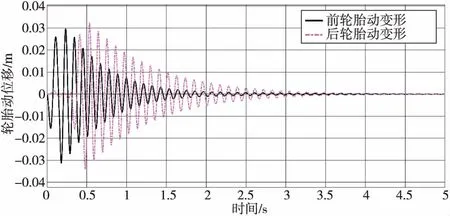
图11 CaseⅡ主动悬架轮胎动位移

4 结论

1)主动悬架H2/H∞控制器能够在统一框架下，同时处理性能指标与鲁棒稳定之间合理折中问题，实现平顺性和操纵稳定性多目标优化控制，克服了其他控制方法在解决该问题时的缺陷。

2)在时域进行仿真，选择合理的γ1值，验证CaseⅠ主动悬架的车身垂直加速度和俯仰加速度的值比被动悬架明显降低。该控制器不仅提高了主动悬架的动态性能，而且改善车辆行驶的舒服性。当选择γ1的值越大，车辆行驶的舒服性得到提高，但操纵稳定性逐步变差，即平顺性的改善是以牺牲操纵稳定性为代价的。γ1的值超过一定值后，系统超调现象加剧，动态性能恶化[10]。

3)主动悬架H2/H∞多目标状态反馈控制器仿真结果表明，该方法能够有效实现对悬架动行程、主动控制力和接地性的性能约束。