地锚式斜拉-悬索协作体系桥竖弯振动基频计算公式
2019-09-17王绪旺
王绪旺
(商洛学院城乡规划与建筑工程学院, 陕西 商洛 726000 )
随着经济和技术的发展,在沿海地区修建大跨度斜拉桥或悬索桥等桥型已经不能满足工程的需要。针对这一迫切需求国内外许多学者提出了斜拉-悬索协作体系。土耳其博斯普鲁斯海峡三桥的建成,标志着该结构体系进入一个新的阶段,开展该结构体系固有振动特性研究具有较强的实用意义[1-7]。文献[8]在计入主塔纵向抗弯刚度影响下,提出了对单跨简支地锚式悬索桥体系的竖弯基频修正的计算表达式;文献[9-11]在考虑主塔纵向抗弯刚度影响下,采用能量法推导了多塔悬索体系的竖弯振动估算实用公式,并提出了中塔纵向抗弯刚度影响系数;文献[12-14]以地锚式斜拉-悬索协作体系桥为研究对象,研究该结构的静动特性及不同约束条件对其力学性能的影响,遗憾的是未能给出相应的理论解。本文以三跨连续体系的地锚式悬索桥为研究对象,在计入主塔纵向抗弯刚度的影响下,采用能量法推导其竖弯振动基频估算实用公式,以供该协作体系桥在初步概念设计阶段选择合理计算参数或对数值计算结果进行复核。
1 基于能量法的地锚式协作体系的竖弯基频估算实用公式
1.1 地锚式斜拉-悬索协作体系的势能
主缆的势能主要由2部分组成,即主缆水平分力变化产生的弹性势能Uce和主缆重力作用点变化引起的重力势能Ucg,即
主缆的弹性势能为:
(1)
(2)
(3)
式中符号如图1所示。
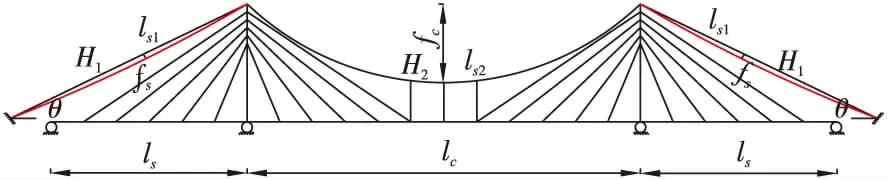
图1 桥跨布置立面
主缆的重力势能为
(4)
式中:v为加劲梁的振型函数;Hq为主缆恒载作用下的水平分力。
拉索的弹性势能为
(5)
式中:EciAci/Lci,αci分别为拉索的单位轴向刚度及水平倾角。
加劲梁的弯曲势能为
(6)
式中:EgIg为加劲梁的抗弯刚度。
(7)
式中:Hi,Hi+1分别为i,i+1号主跨的主缆的水平分力;Sti为第i号主塔的抗弯刚度。
该协作体系的势能为上述各构件的势能之和,即
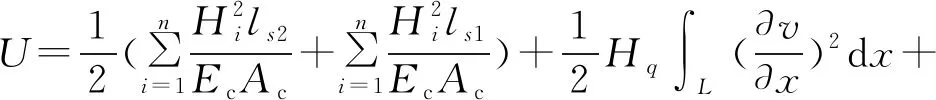
(8)
1.2 地锚式斜拉-悬索协作体系的动能
(9)
式中:mc为主缆的单位桥长质量。
(10)
式中:mg为加劲梁的单位桥长质量。
主塔的动能为
(11)
式中:mti为第i号主塔的质量。
(12)
式中:mhi为第i号吊索的质量。
(13)
式中:mci为拉索的线均布质量。
该协作体系的动能为上述各构件的动能之和,即
(14)
1.3 地锚式斜拉-悬索协作体系的竖弯频率计算表达式
由能量法可得,地锚式斜拉-悬索协作体系桥的竖弯频率计算表达式为
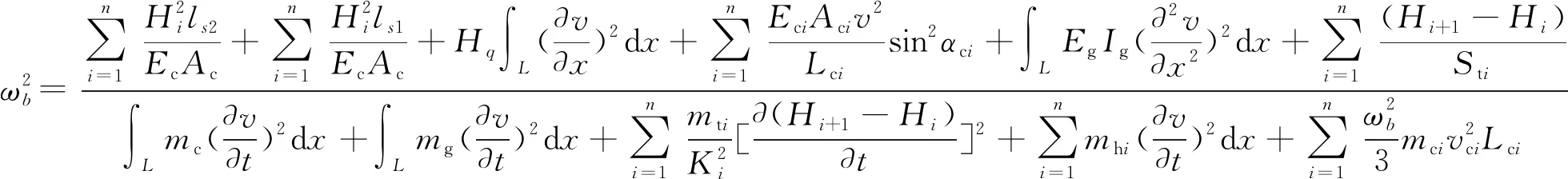
(15)
根据文献[12-14]研究成果,可将式(15)简化为
(16)
2 地锚式协作体系的变形协调方程
地锚式协作体系的一阶竖弯基本振型如图2、图3所示。
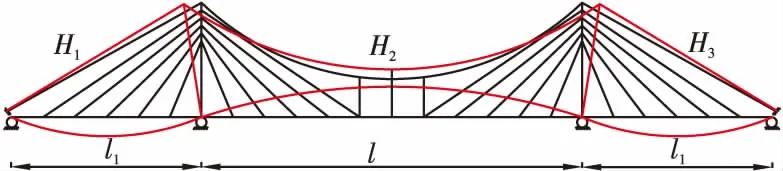
图2 地锚式协作体系的1阶对称竖弯振型
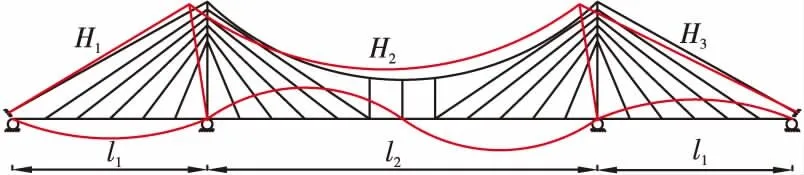
图3 地锚式协作体系的1阶反对称竖弯振型
2.1 地锚式协作体系的1阶对称竖弯变形协调方程
该协作体系做1阶对称竖弯振动时的边、主跨的变形协调方程分别为
(17)
(18)
式中,ut为该体系做1阶对称竖弯振动的主塔的位移。
该协作体系做1阶对称振动时,主塔的受力计算图示如图4所示。

图4 地锚式协作体系1阶对称主塔受力示意图
其力学平衡方程为
(19)
式中,EtIt,ht为主塔的抗弯刚度、高度。
联立求解式(17)—(19),可得:
(20)
(21)
2.2 地锚式协作体系的一阶对称竖弯变形协调方程
该协作体系做一阶反对称竖弯振动时的边、主跨变形协调方程分别为:
(22)
(23)
(24)
该协作体系做一阶反对称竖弯振动时,主塔的受力如图5所示。

图5 地锚式协作体系1阶竖弯反对称主塔受力示意图
其力学平衡方程为:
H2+Stut=H1
(25)
H3+Stut=H2
(26)
联立求解式(22)─(26),可得:
(27)
(28)
(29)
3 地锚式协作体系的一阶对称竖弯基频计算式
加劲梁1阶对称振型关于中跨跨中对称如图2所示,设加劲梁的自由振动振型函数为:
(30)
(31)
由于加劲梁的振型函数在桥塔处满足变形协调条件,可得
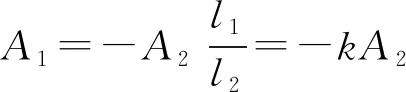
(32)
于是,可得
(33)
式中:λ为主塔刚度影响系数。
(34)
(35)
(36)
(37)
(38)
将式(33)—(38)代入式(16),可得其的一阶竖弯对称基频的计算式为
(39)
4 地锚式协作体系的一阶反对称竖弯频率计算式
加劲梁一阶反对称振型关于中跨跨中反对称如图3所示,设其加劲梁的自由振动振型函数分别为:
(40)
(41)
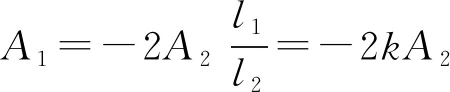
(42)
于是,可得:
(43)
(44)
(45)
将式(43)─(45)代入式(16),可得其一阶反对称竖弯基频的计算式为
(46)
5 算例分析
为验证本文解的计算精度,本文以文献[14]中的算例为例进行校核。该桥跨径布置为319 m +1 400 m +319 m。结构计算参数及计算结果如表1、2所示。
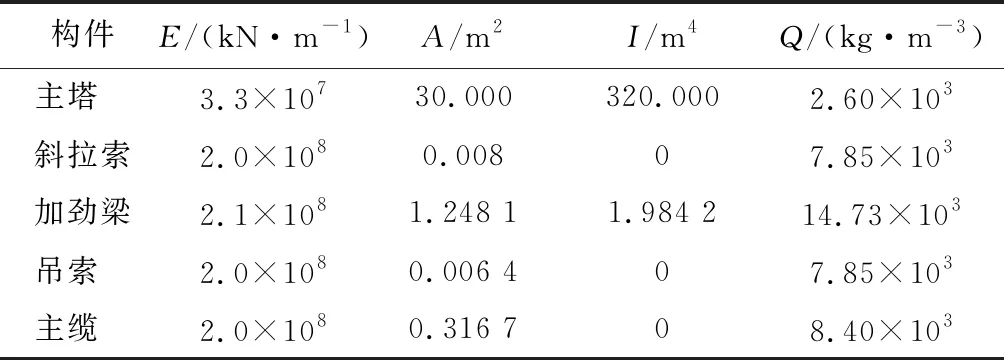
表1 结构计算参数
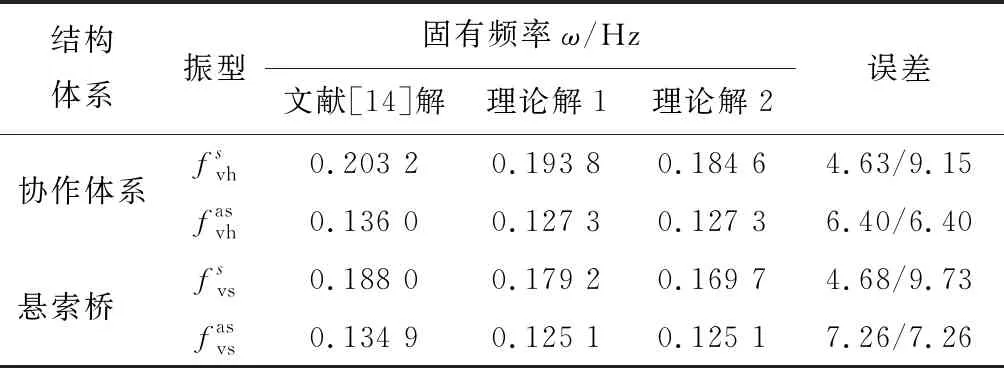
表 2 不同计算方法结果比较
注:“/”前为文献[14]与理论解1的误差,理论解1为计入主塔抗弯刚度的结构体系的竖弯基频;“/”后为文献[14]与理论解2的误差,理论解2为未计入主塔抗弯刚度的竖弯基频
算例分析表明,在计入主塔抗弯刚度影响下,理论解1法与文献[14]法计算得到的该体系的竖弯振动基频的计算误差在5%左右;在未计入主塔抗弯刚度影响下,理论解2与文献[14]解之间的误差最大为9.15%。存在上述误差的根本原因是该协作体系的实际振型函数与本文假设的加劲梁的振型函数存在一定差异造成的;理论解1的对称竖弯基频计算精度相对理论解2的计算精度要高,其原因在于理论解1中计入主塔纵向抗弯刚度的影响。同时不难发现,该协作体系的基频比同等跨径布置的悬索体系的基频略大,其原因在于在协作体系中,计入拉索对结构体系的影响。
6 结论
1)地锚式协作体系桥梁竖向弯曲振动动力特性是由缆索结构决定的。该体系的竖向弯曲振动基频较同等跨径布置的地锚式悬索桥的竖弯弯曲基频要略大,其原因在于斜拉索对该协作体系的刚度的贡献。
2)本文利用加劲梁自由振动的振型函数在桥塔处满足变形协调条件,采用能量法推导了该协作体系的竖弯振动频率估算实用公式,此式可用于该协作体系桥梁在初步设计阶段选取合理的计算参数或对数值计算结果进行复核。
3)本文所推导的竖弯振动基频估算实用公式仅仅适用于三跨连续支承体系的地锚式协作体系桥梁的竖弯基频估算,对其他协作体系的竖弯振动基频估算并不适用。为进一步提高所推导的计算公式的计算精度,在后续的研究中可考虑纵飘振动对竖弯振动的影响,以便提高计算精度。
