一种半主动动力吸振器参数优化及性能比较
2019-09-17申永军杨绍普
郎 君, 申永军, 杨绍普
(石家庄铁道大学 机械工程学院,石家庄 050043)
动力吸振器(Dynamic Vibration Absorber,DVA)是一种加装在主系统上控制振动的吸振装置。自1909年Frahm[1]发明DVA以来,动力吸振器经历过一百多年发展,不断优化改进,如今在高大建筑、桥梁、机械设备、交通工具等诸多领域有着广泛应用。动力吸振器经历了被动控制、半主动控制、主动控制三个发展阶段。被动式动力吸振器因其结构简单且可靠性高,目前应用最为广泛。Ormondroyd等[2]最早提出带有阻尼的Voigt型动力吸振器,并先后由Hahnkamn[3]和Brock[4]给出该模型最优频率比和最优阻尼比公式。Asami等[5-6]提出三要素型动力吸振器,发现在同样质量比情况下,三要素型动力吸振器要比Voigt型动力吸振器效果更好。Ren[7]提出一种将吸振阻尼接地的新型动力吸振器,王孝然等[8]又将其拓展为弹簧阻尼串联接地的动力吸振器。研究表明以上两种动力吸振器吸振效果均优于Asami的三要素型动力吸振器。主动式动力吸振器较被动式动力吸振器多了可调致动器,按控制原理可分为调频式和非调频式。调频式动力吸振器包括磁浮式[9]、电动式[10-13]、电磁弹簧[14-15]等类型。非调频式动力吸振器包括主动变刚度[16-18]、主动变质量阻尼系统[19-22]和智能材料(如磁流变弹性体)[23]控制等。半主动动力吸振器是将吸振器的结构刚度或者阻尼进行实时调节以改善主系统振动的吸振器。依据控制原理,可分为变刚度式动力吸振器和变阻尼式动力吸振器。Brennan[24]设计了一种变刚度空气弹簧动力吸振器。Williams等[25-26]设计了一种变刚度记忆合金动力吸振器。
近年来,学者对半主动控制策略研究也有很大进展。Liu等[27]提出基于“天棚”系统的Continuous Skyhook、On-off Skyhook、Continuous Balance和On-off Balance四种半主动变阻尼控制策略。Koo等[28]为抑制建筑结构振动,提出了两种半主动变阻尼吸振控制策略——半主动开关速度-速度控制(Velocity-based on-off ground-hook control,On-off VBG)策略和半主动开关位移-速度控制(Displacement-based on-off ground-hook control,On-off DBG)策略。
本文将Koo的两种离散半主动控制策略,半主动开关速度-速度控制(On-off VBG)策略和半主动开关位移-速度控制(On-off DBG)策略,应用到Voigt型吸振器中。首先,建立系统模型,确定参数取值范围。然后,对两种半主动控制吸振系统进行参数优化和参数影响性分析。最后,引入随机激励对不同类型吸振器进行吸振效果对比。结果显示半主动开关位移-速度控制(On-off DBG)策略下主系统位移方差最小。验证了半主动开关位移-速度控制(On-off DBG)策略的有效性。
1 动力吸振器模型及系统基本参数
将传统Voigt模型(图1(a))进行改进,得到半主动变阻尼式动力吸振器(图1(b))。其中主系统质量为m1,吸振器质量为m2,主系统刚度为k1,吸振器刚度为k2,阻尼器阻尼系数为c2,主系统位移为x1,动力吸振器位移为x2,外加力激励为F0cos(ωt)。

(a) Voigt型吸振器
系统基本参数如表1。
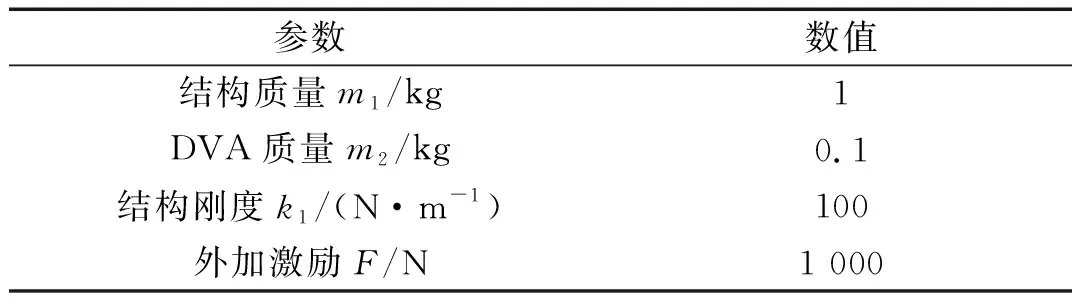
表1 系统主要参数
半主动控制动力吸振器的阻尼分为On和Off两个状态,对应的阻尼分别记做ζ2max,ζ2min。ν是ω2与ω1之比。根据工程实际,半主动On-off控制系统各参数取值范围如表2。
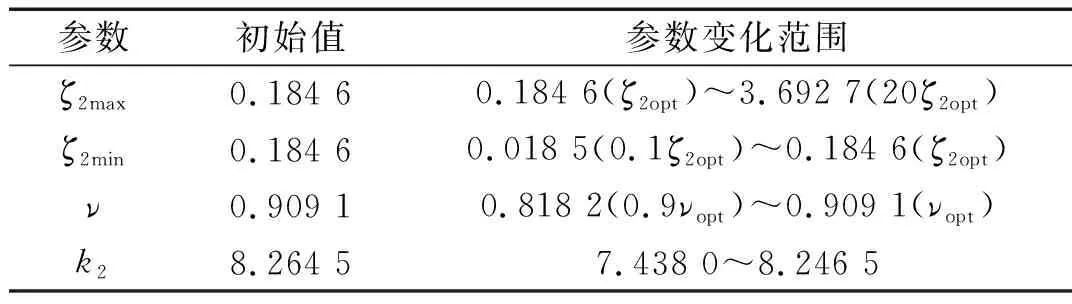
表2 各参数的初始值及取值范围
需要说明,表2中各参数取值范围,虽参照文献[28],也按连续形式给出,但本文将各优化参数与被动Voigt型吸振器最优参数联系起来,使其和传统Voigt型吸振器参数对比明显。
2 系统参数优化及效果比较
被动式动力吸振器优化方法有多种,常见的有H2优化和H∞优化,这些优化理论都很成熟。但是,对于半主动控制动力吸振器,优化理论还不完善。目前,只能以实验或者数值仿真的方式进行优化。本文中通过调节参数,对比不同参数下系统幅频曲线,找到参数范围内最优控制效果和对应参数,并对其中的关键参数进行特性分析。
根据系统模型,建立系统的动力学方程

(1)
两种半主动开关控制策略分别表示:半主动开关速度-位移控制(On-off VBG)策略
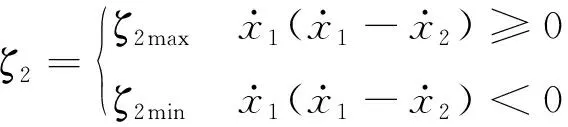
(2)
半主动开关位移-位移控制(On-off DBG)策略
(3)
利用四阶龙格-库塔法对不同控制策略下的系统求解并进行参数优化。参数优化过程中,调整主要参数值,不同控制策略的最终优化结果如图2所示。结果显示,两种半主动控制策略吸振效果有较大差异:半主动开关速度-位移控制(On-off VBG)策略主系统的响应与被动控制效果差异不大;半主动开关位移-位移控制(On-off DBG)策略主系统的响应明显降低。综合对比两结果,可以认为半主动开关位移-位移控制(On-off DBG)策略能有效降低主系统振动。
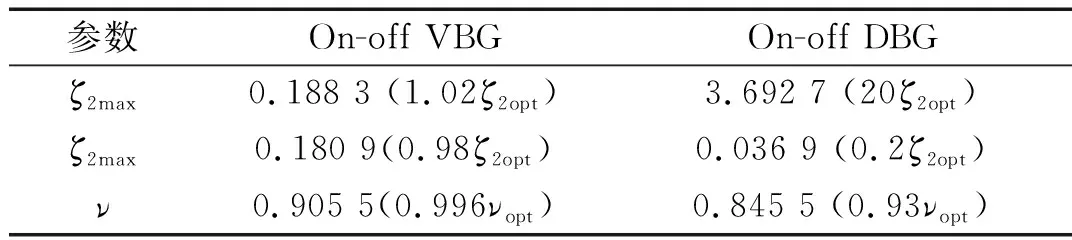
图2中,两种半主动Voigt型动力吸振器最优吸振效果对应参数,在表3中列出。
半主动开关位移-位移控制(On-off DBG)控制策略中,有三个参数对优化效果起关键作用,它们分别是开
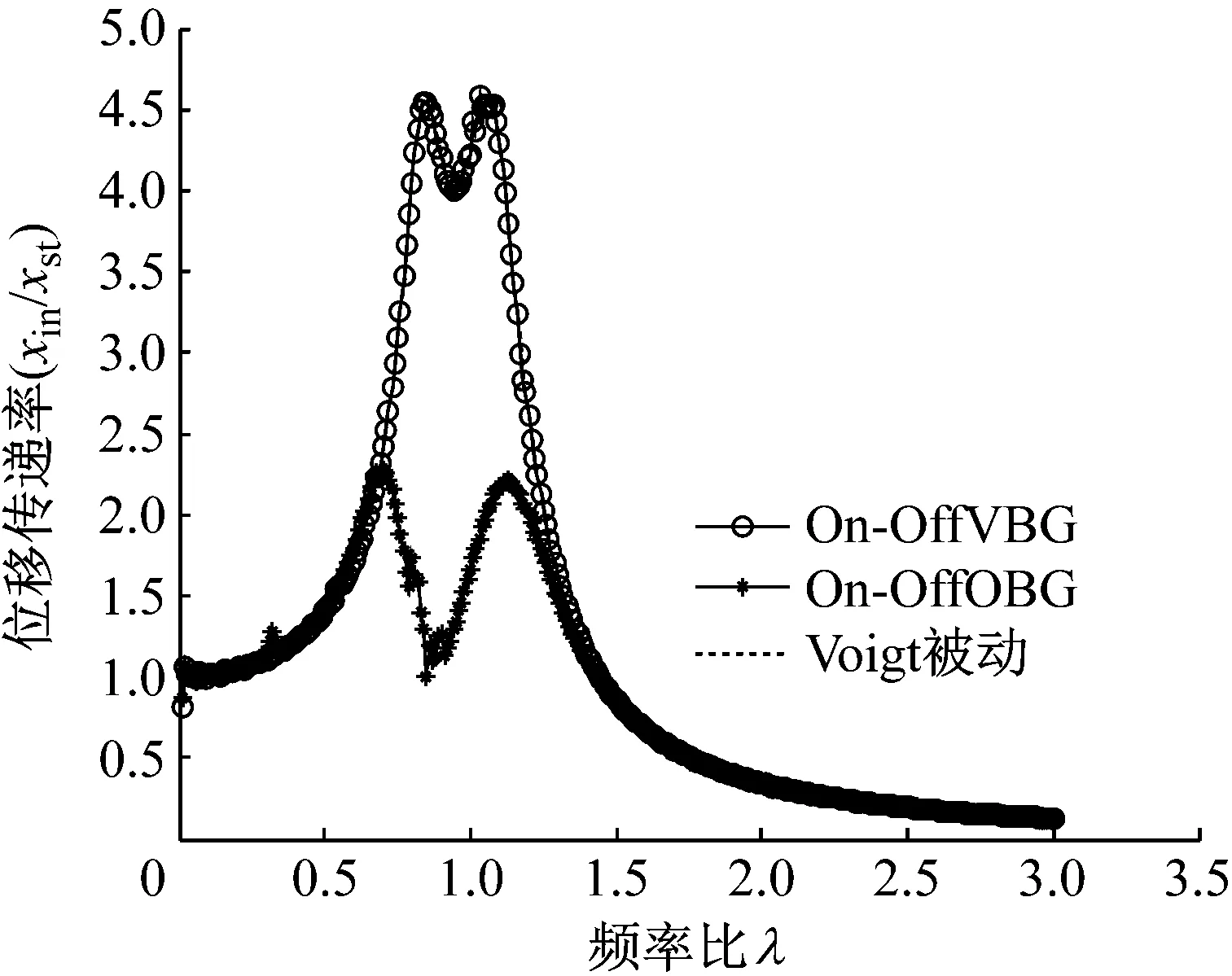
图2 Voigt模型两种半主动控制策略与被动控制策略对比
参数On-off VBGOn-off DBGζ2max0.188 3 (1.02ζ2opt)3.692 7 (20ζ2opt)ζ2max0.180 9(0.98ζ2opt)0.036 9 (0.2ζ2opt)ν0.905 5(0.996νopt)0.845 5 (0.93νopt)
状态阻尼比、关状态阻尼比和频率比。下面分别研究三者在半主动开关位移-位移控制(On-off DBG)策略下对幅频曲线的影响(说明:图6~图10中参数ζ2max、ζ2min和ν后面的数字均表示为ζopt或νopt的倍数)。
2.1 开状态阻尼比ζ2max的影响
图3是开状态阻尼比ζ2max对幅频曲线的影响。从图中可以看出,随着开状态阻尼比ζ2max增大,幅频曲线两峰下降明显。对幅频曲线具体影响总结如下:
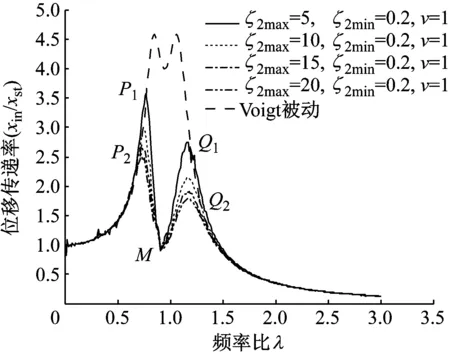
图3 开状态阻尼比ζ2max影响
(1) 显著降低幅频曲线峰值。随着ζ2max增大,幅频曲线两峰P、Q均显著降低。ζ2max由0.923(5ζopt)增至3.629(20ζopt),P峰由P1=3.569降到P2=2.547,Q峰由Q1=2.747降到Q2=1.790。
(2) 不影响谷底M。在ζ2max增大过程中,幅频曲线谷底M未变,即ζ2max变化不影响谷底M。
(3)ζ2max呈非线性降低两峰值,即在增大相同ζ2max时,ζ2max降低幅频曲线两峰能力逐渐减弱。开始时ζ2max由0.923(5ζopt)增至1.846(10ζ2opt),P、Q两峰分别降低0.639、0.610;但是当ζ2max由2.769(15ζ2opt)增至20ζ2opt时,P、Q两峰只分别下降0.150、0.116,后者峰值降低量明显小于前者。因此,不能为获得更低峰值而不加限制增大ζ2max值。
2.2 关状态阻尼比ζ2min的影响
图4是关状态阻尼比ζ2min对幅频曲线的影响。从中可以看出,随着ζ2min减小,幅频曲线峰值降低明显。具体影响总结如下。
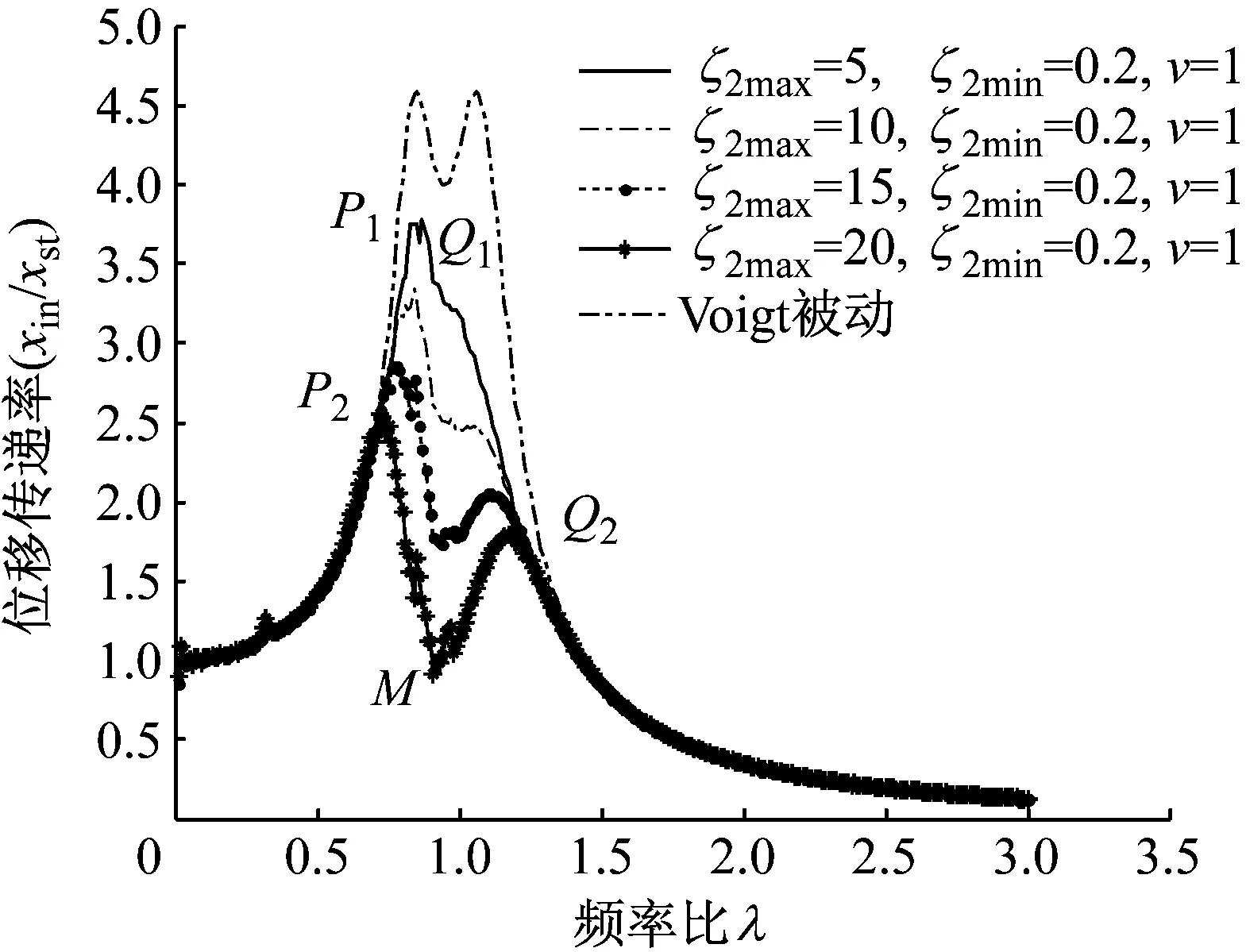
图4 关状态阻尼比ζ2min影响
(1) 显著降低幅频曲线峰值。随着ζ2min减小,幅频曲线两峰P、Q降低明显。ζ2min由0.148(0.8ζopt)降至0.037(0.2ζopt),P峰由P1=3.744降至P2=2.541,Q峰由Q1=3.211降至Q2=1.790。ζ2min与ζ2max特性正好相反。
(2) 明显影响谷底M。系统处在大阻尼状态时(ζ2max=3.692 7和ζ2min=0.184 6),两峰汇聚到一起,影响半主动动力吸振器性能。随着ζ2min减小,谷底M迅速降低,降低两峰同时也加大两峰的间距。这间接增大了系统有效工作带宽,对系统稳定性有很好的提升。
(3) 过小ζ2min会引起系统不稳定振动。虽然已知降低ζ2min能有效降低谷底M,但ζ2min过小,会使幅频曲线在谷底产生突变尖峰,发生不稳定振动(如图5),这对机械设备会产生严重损害。因此,不能为追求低峰值而不加限制的降低ζ2min值。本系统中,半主动Voigt型动力吸振器的ζ2min不能低于0.037 (0.2ζ2-Off)。
2.3 频率比ν的影响
图6是频率比ν变化对幅频曲线的影响。选取不用频率比ν,分析其对幅频曲线的影响。
从图中可以看出频率比ν对幅频曲线的影响:
(1) 有效降低两峰,且对两峰作用相反。随频率比ν增大,P峰由P1=2.235增至P2=2.547。Q峰由Q1=2.335降至Q2=1.790。正是频率比ν对P、Q两峰相反作用,使得我们能找到系统最优幅频曲线。
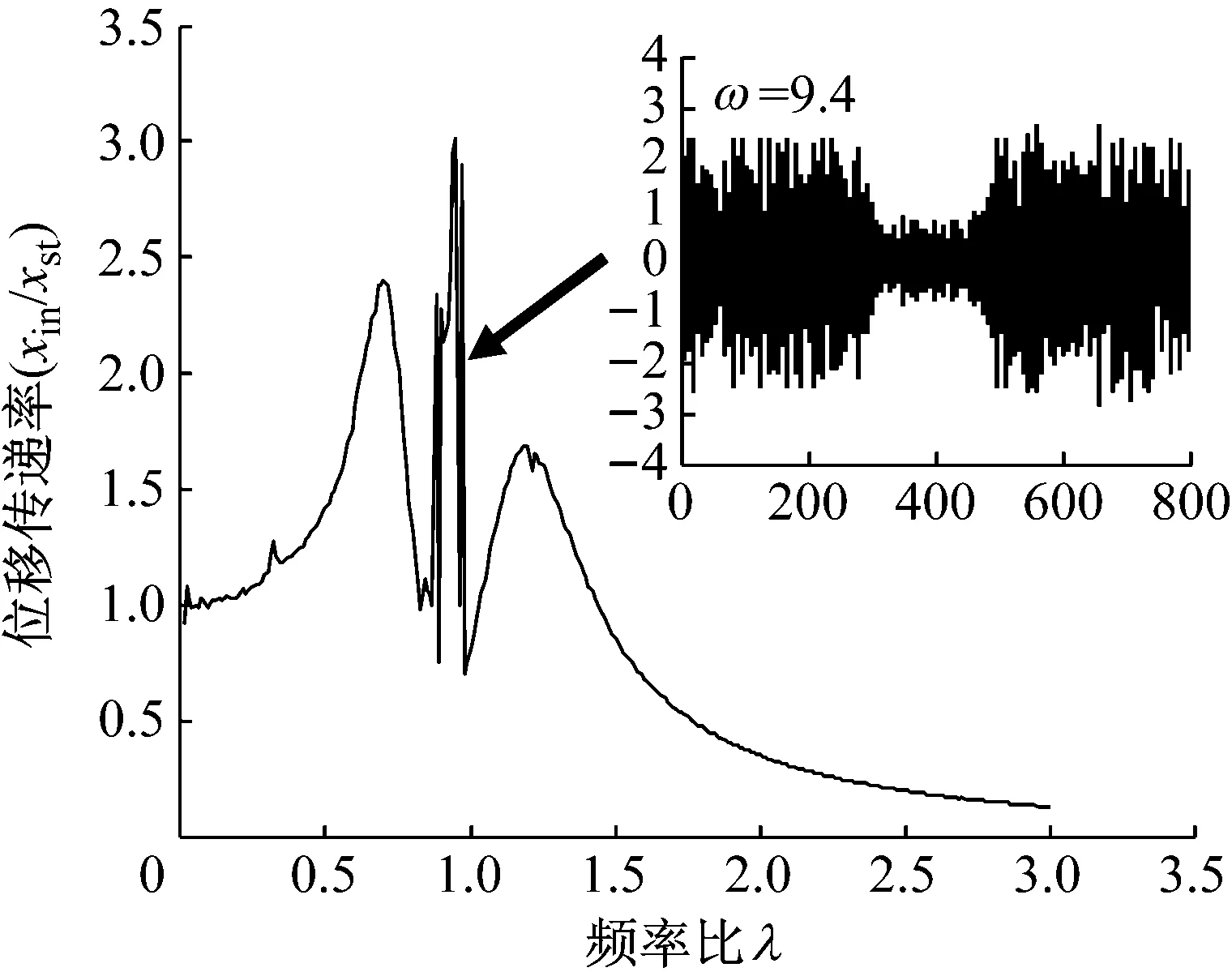
图5 ζ2min过小引起不稳定振动
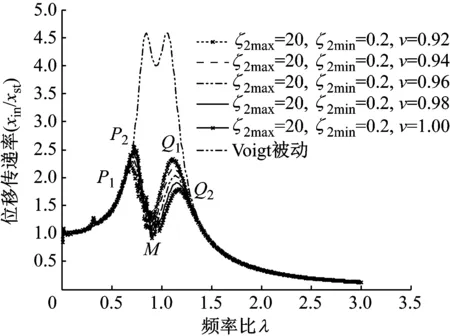
图6 频率比ν影响
(2) 轻微影响谷底M。随频率比ν增大,谷底值变化小于0.2,对谷底影响轻微。同时,P、Q两峰横向间距0.44~0.45之间,对系统有效稳定带宽影响也不大。
2.4 三个参数综合作用最优结果
根据三个关键对幅频曲线的影响特性,利用数值法可以获得系统的最优控制幅频曲线。不同参数值下半主动开关位移-位移控制(On-off DBG)控制Voigt型吸振器的最优幅频曲线,如图7所示。参数范围内,系统最优幅频曲线的P峰为2.247,Q峰为2.216(参数:ζ2max=20ζopt,ζ2min=0.2ζopt,ν=0.93νopt)。
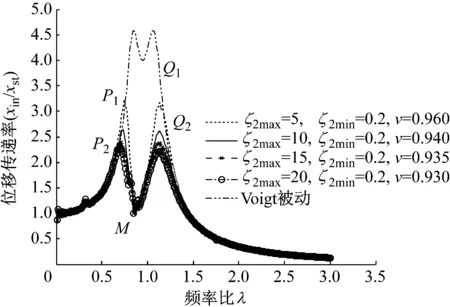
图7 不同参数下半主动On-off DBG最优控制效果
3 系统随机激励下的响应
在实际工程中,建筑结构受到的外力多以随机激励为主,因此对振动系统进行随机激励响应研究具有实际意义。除上文中提到的两种振动模型,还引入不含吸振器的单自由度系统和被动Voigt型动力吸振系统作对比。通过对比不同模型的随机激励响应,比较各吸振器的减振性能。
选取50 s的均值为0方差为1的随机激励,其时间历程如图8。系统参数按照表1~表3中选取。图9为不含吸振器主系统时间历程,图10为被动Voigt型吸振器主系统时间历程,图11为半主动开关速度-位移控制(On-off VBG)策略Voigt型吸振器主系统时间历程,图12为半主动开关位移-位移控制(On-off DBG)策略Voigt型吸振器主系统时间历程。
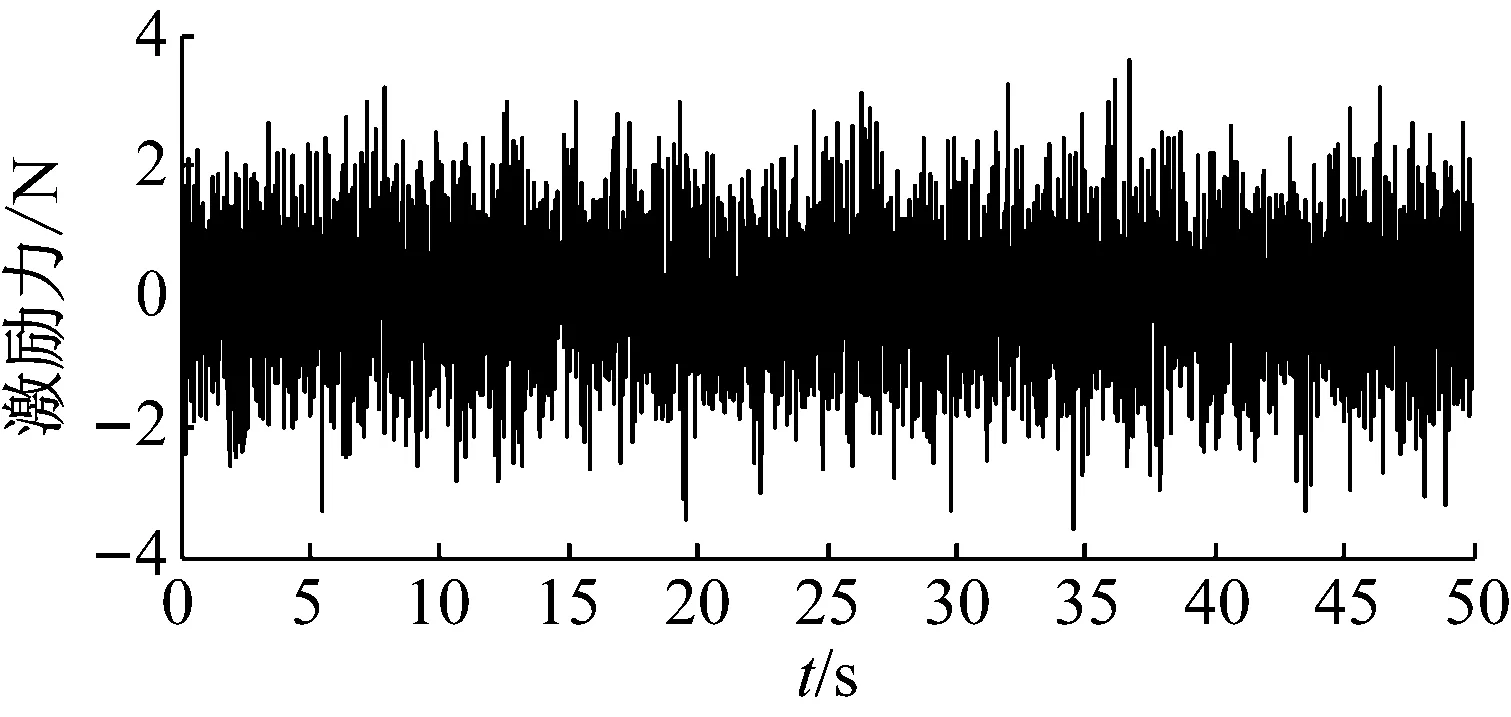
图8 随机激励
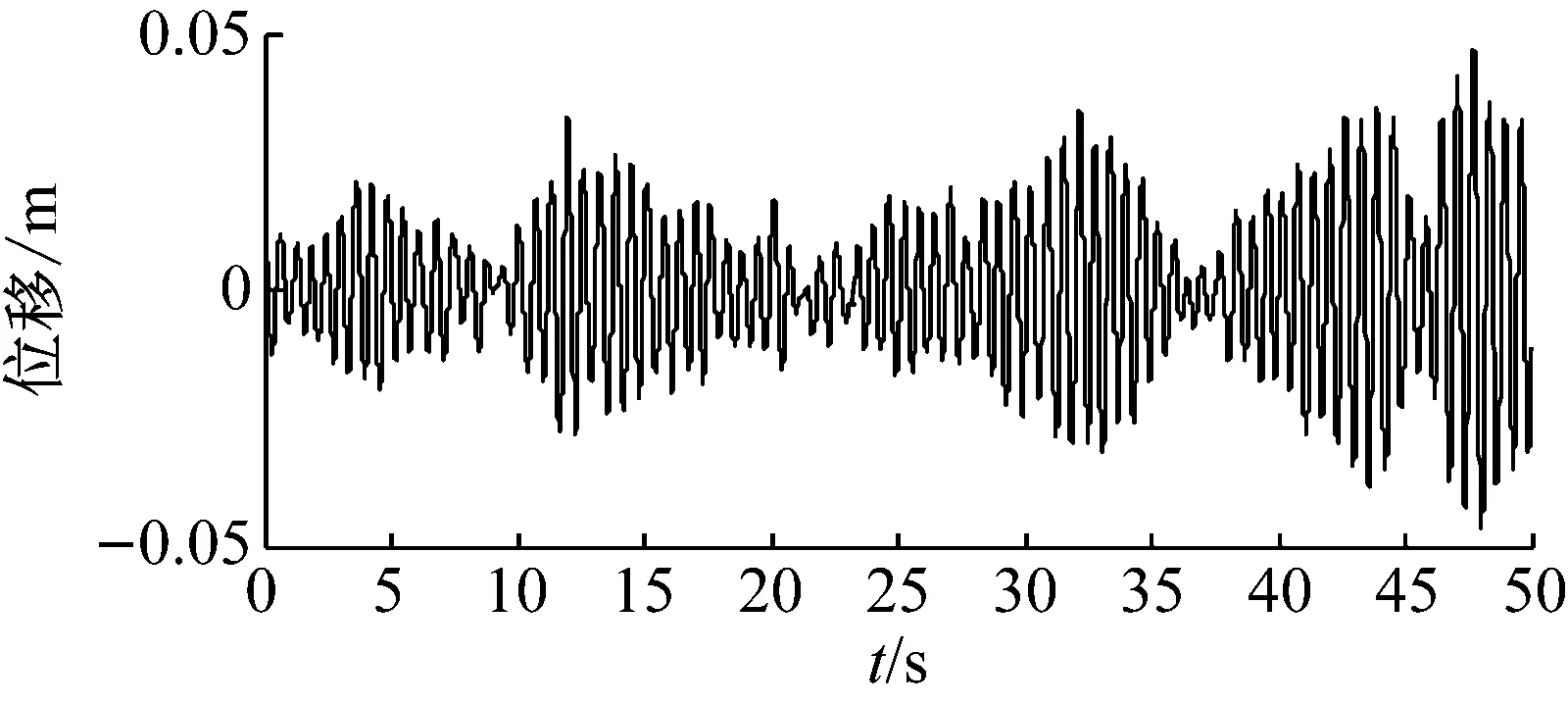
图9 不含吸振器的主系统时间历程
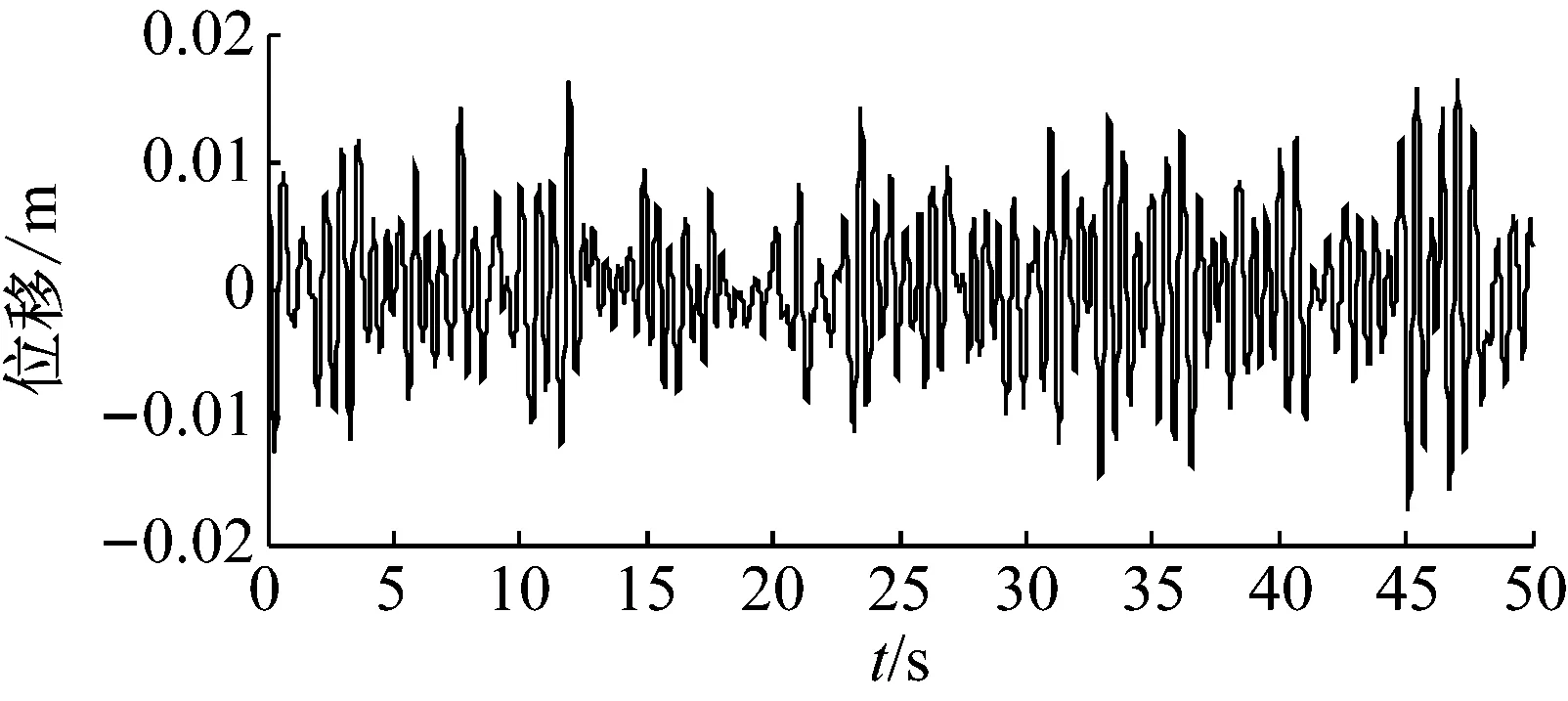
图10 被动Voigt型吸振器的主系统时间历程
结合不同类型的吸振器主系统时间历程(图9~图12)及表4,可以看出半主动开关位移-位移控制(On-off DBG)策略吸振器对主系统的减振效果要明显优于其它类型动力吸振器。其主系统位移方差衰减率达到91.07%,减振效果显著。因此,半主动开关位移-位移控制(On-off DBG)策略Voigt型吸振器优于其他类型动力吸振器。
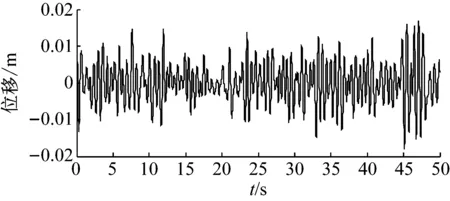
图11 半主动开关速度-位移控制(On-off VBG)吸振器主系统时间历程
Fig.11 The time history of the primary system with dynamic vibration absorber under semi-active On-off VBG strategy
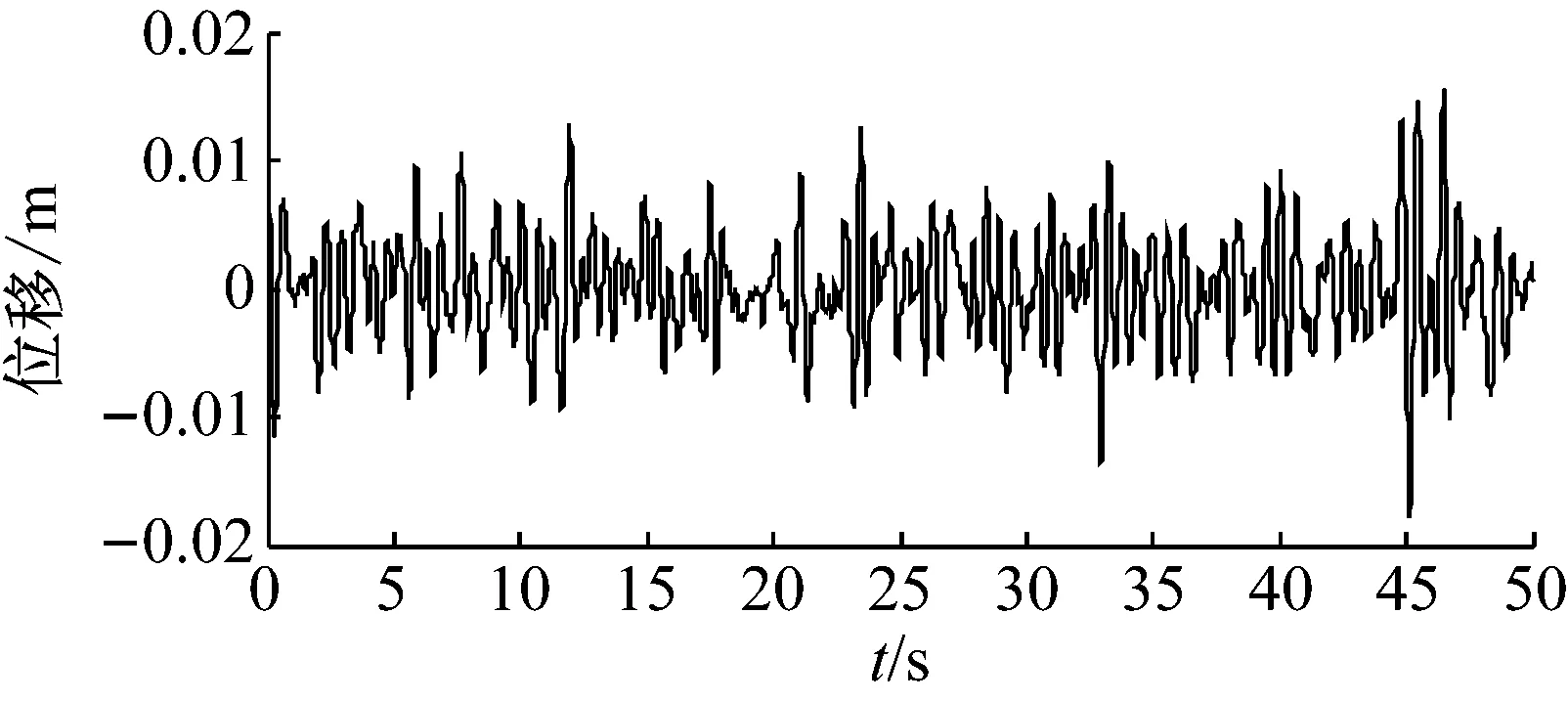
图12 半主动开关位移-位移控制(On-off DBG)吸振器主系统时间历程
Fig.12 The time history of the primary system with dynamic vibration absorber under semi-active On-off DBG strategy
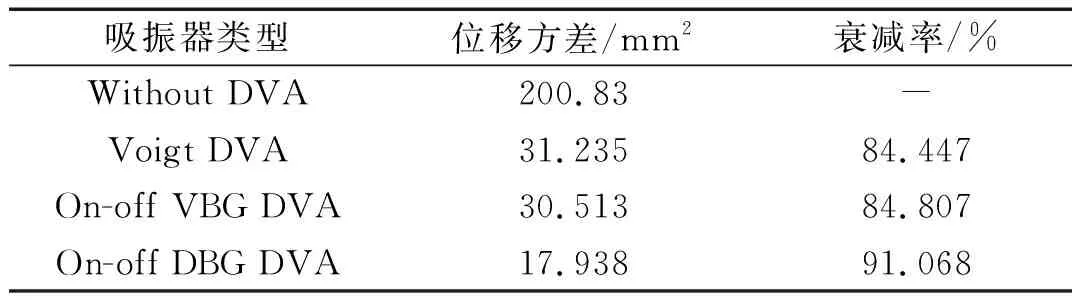
表4 主系统位移方差及衰减率
4 结 论
论文将两种半主动开关控制策略应用到Voigt型动力吸振器中,确定了半主动开关位移-速度控制(On-off DBG)策略的有效性。其次,对影响半主动开关位移-速度控制(On-off DBG)策略的3个关键参数:开状态阻尼比、关状态阻尼比和频率比进行了特性研究,找到了在参数允许变化范围内具有最优控制效果的参数值。由于目前条件所限,不能实现本论文中提出的实验模型验证,故而采用随机激励间接验证模型的半主动控制吸振效果。在随机激励吸振效果验证中,不同控制策略下吸振器的随机激励响应不尽相同,发现半主动开关位移-速度控制(On-off DBG)策略的主系统位移响应方差值最小。可以认为半主动开关位移-速度控制(On-off DBG)策略是一种有效的半主动控制策略。关于模型吸振效果的实际验证,将是后续工作中的研究重点。
