基于整周期时域回归识别滚子间距变化的保持架故障诊断方法
2019-09-17李修文唐德尧杨荣华
李修文, 唐德尧, 杨荣华
(1.唐智科技湖南发展有限公司,长沙 410083;2.北京唐智科技发展有限公司,北京 100038)
各类机械设备中旋转机械约占设备的80%[1],其常见的故障模式,如齿轮、轴不平衡、不对中、轴承外环、内环、滚子类故障,诊断方法较为成熟,主要有傅里叶频谱分析法、幅域分析法、小波分析法、EMD、Hilbert变换以及SVM、神经网络、遗传算法等模式识别方法[2-4],当前国内外的研究方向主要集中在如何在故障早期发现故障、如何提取复杂信号中的微弱故障特征信息,这类方法主要有声发射分析法、S变换、非线性时间序列分析法、数学形态学、随机共振、混沌理论等[5-10],这其中轴承保持架的故障,由于保持架公转频率极低,其特征频率一般位于频谱图上的最左端,容易被低频干扰所混淆,并且工程实际应用中易受数据长度的限制、频率分辨率较大,容易出现频谱的能量泄露现象,往往不易识别和发现此类故障,因此,对于保持架的故障诊断一直是轴承故障诊断中的难点[11-12]。尽管有部分学者专门对保持架的故障诊断方法进行了相关研究,如提出了基于小波分析的诊断方法[13]、基于共振解调的外孤谱诊断方法[14]等,但这些方法仍然是基于金属保持架故障或破碎物对金属外环、内环(或其挡边)碰撞或摩擦而发生冲击信息的原理,其中外孤谱主要是识别油脂中是否存在杂质,且实际应用于保持架的故障诊断效果均有限。
随着塑料保持架的快速发展,近年来工程塑料保持架的应用越来越广泛[15],从树脂材料所具有的高弹性、自润滑性、耐磨性、耐冲击性、耐蚀性、易加工性和轻量化等方面来讲,工程塑料保持架在很多方面都有利于改善轴承的性能,如轨道交通领域,就出现了大量使用非金属保持架(如尼龙保持架)轴承取代金属保持架轴承的情况,由于塑料保持架发生故障后无法像金属保持架那样产生金属碰撞从而引发冲击信息,使得传统的基于保持架特征频率的方法几乎完全失效。为此,本文提出了一种基于整周期时域回归的方法,能够有效提取到反映各滚子间隔是否异常的信息,本方法不仅适用于非金属保持架的故障诊断,同样也适用于金属保持架的故障诊断。
1 滚子通过外环应力所致振动信号特征
轴承在运转中,保持架携带各个滚子逐个通过轴承承载区时,如果轴承的内、外环和滚子没有故障,则由于单个滚子承受载荷而使轴承的外环产生应变应力而导致振动;当存在外环故障或杂质时,则主要因滚子逐个通过外环故障的突变应力而导致振动,通过所测振动加速度信号中含有的由滚子承受载荷而使轴承的外环产生应变应力信号,通过对轴承的有限元建模仿真,如图1(a)所示,模拟外环固定内环转动,施加一垂直向下的载荷(承载区位于轴承下方),分析滚子通过外环的应力分布,如图1(b)所示(图中将内环、保持架及滚子进行了隐藏设置),可以看出明显的各滚子通过外环的应力变化特征,图1(c)是外环下方某单元格输出的应力随时间的变化特征曲线,如果能够利用高灵敏度传感器获取这种应力变化所致的振动信号,就可以通过分析各滚子通过传感器所在测点(位于承载区)引起的振动变化规律,分析各滚子分布是否异常,从而识别如保持架兜孔磨损超限、保持架窗梁折断未失、保持架窗梁折断失落和因保持架窗梁连续大量失落而发生的滚子乱序等保持架故障。
2 整周期时域回归原理及步骤
旋转机械的故障诊断主要包括故障的定性与定量:定性指定位故障的具体部分或故障类型,定量指确定相应故障的严重程度。
目前,旋转机械故障定性主要是基于特征频率的识别方法,即根据机械结构及其相互间运动学关系推导出的各部件出现故障后,该故障点通过其它与之接触的部件的重复频率,如轴承内外环、滚子、保持架、齿轮、轴、轨道交通车轮的踏面等都有确定的重复通过频率,识别的主要方法是利用傅里叶算法将采集到的时域信号(振动、冲击或声音)转换至频域,通过分析是否出现相应的特征频率从而对故障进行定性。

(a)轴承有限元仿真模型

(b)外环应力分布图
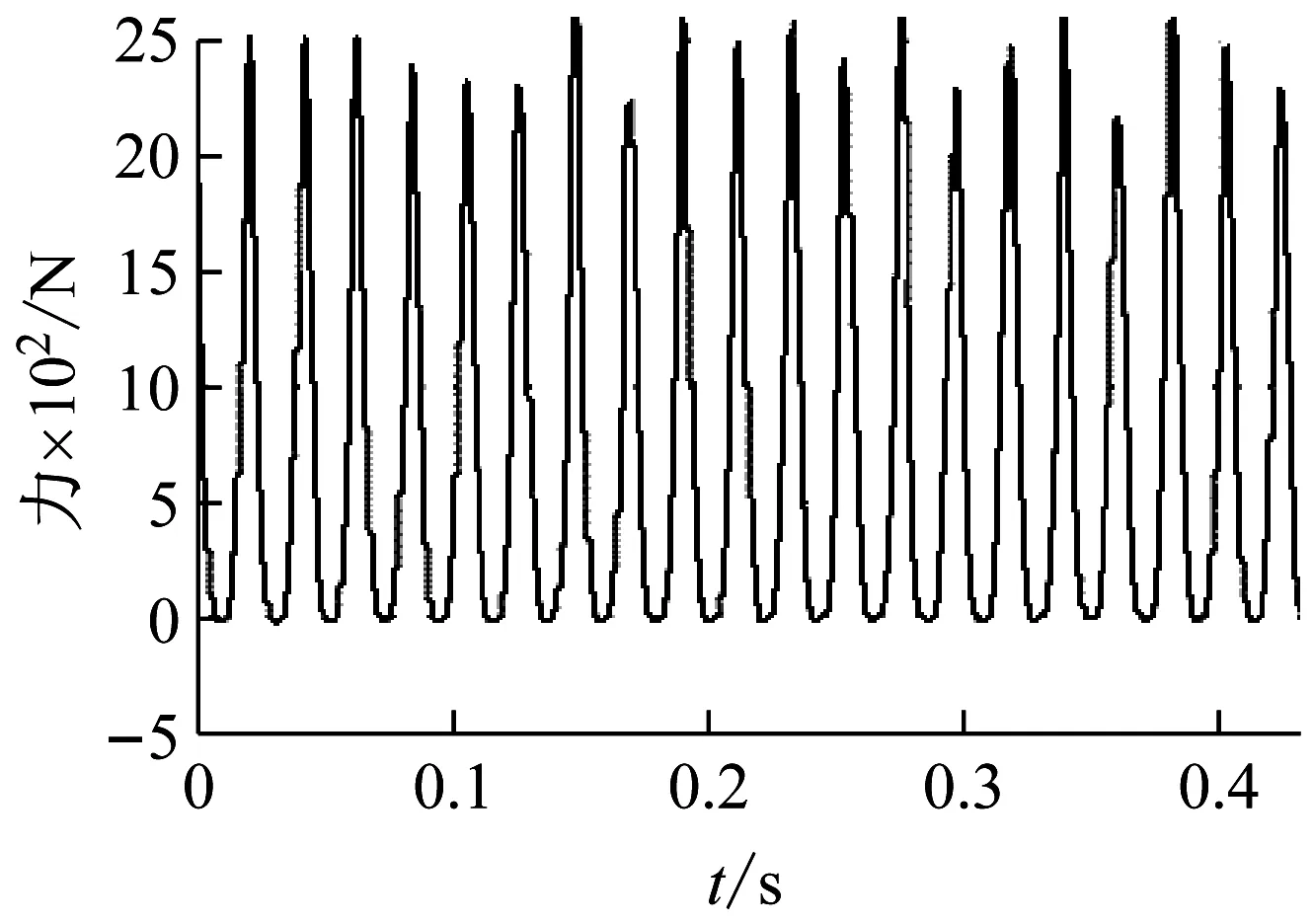
(c)外环应力变化曲线
上述定性方法存在的问题是:如果采样总时长(点数)不等于特征频率Ft对应的特征周期Tt=1/Ft的整数倍,由于存在频率分辨率问题及频域谱号的离散性,会出现特征频率(谱号)处并无谱线,其能量出现在其相邻的、满足整数倍分辨率的谱线上,即出现频谱泄露现象,影响真实特征频率测量的准确性及其能量的真实性。如图2所示,3个仿真信号:信号1为18 Hz、幅值为1的正弦波,信号2为10.24 Hz、幅值为1 000 m(1 000 m=1)的正弦波,信号3为信号1与信号2的叠加即两正弦波叠加,采样时长T=2 s,由分辨率的计算公式可得到频谱分辨率Δf=1/T=0.5 Hz,即FFT分析得到的频谱只有在0.5的整数倍处存在谱线。


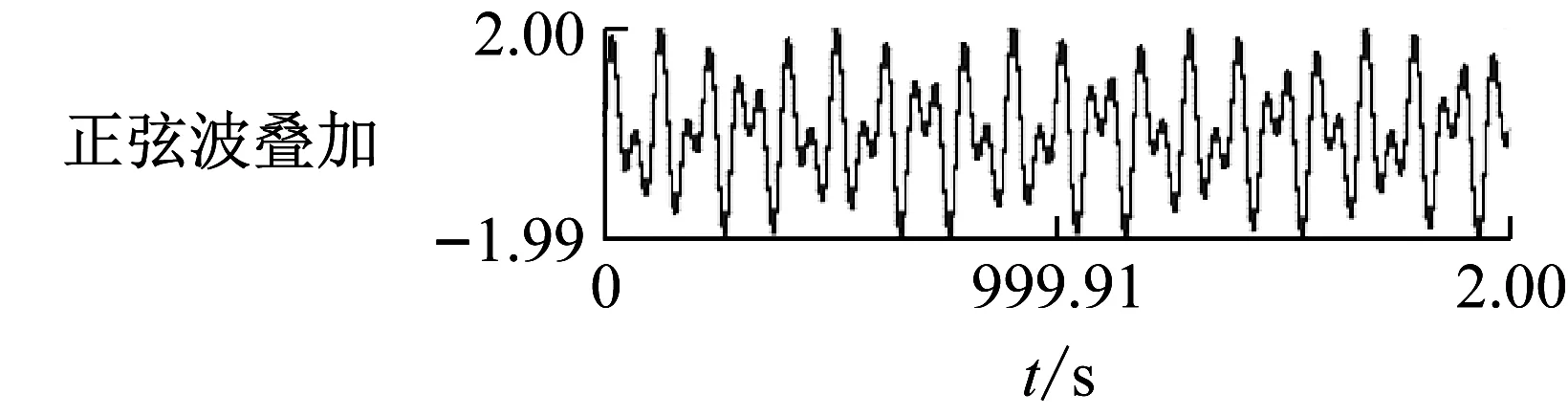
图2 3个仿真信号
图3是图2对应的频谱图,可以看出,由于18 Hz等于0.5 Hz的整数倍,其频谱图可以准确找到18 Hz对应的谱线及相对准确的幅值0.999 64,但10.24 Hz不等于0.5 Hz的整数倍,其频谱图只能找到左右相邻的只在0.5 Hz的整数倍存在的谱线10 Hz及10.5 Hz,其幅值分别为0.67和0.6,与实际值1相关较大。
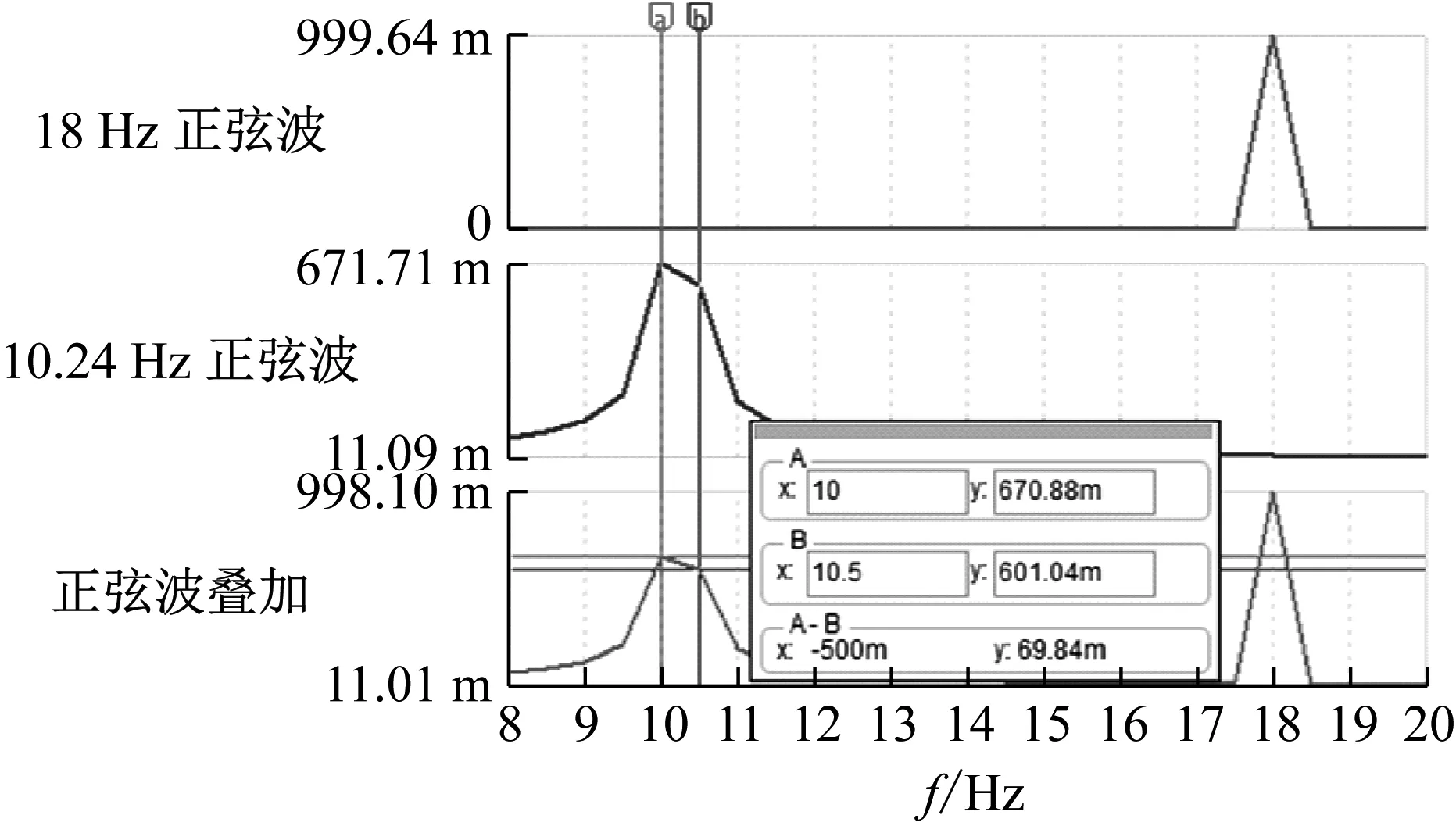
图3 图2对应信号的频谱图
从图3可以看出,由于采样数据长度不满足信号频率的整数倍周期,会出现明显的能量泄露现象,造成频率值与幅值均不准确。有学者提出了利用硬件自适应修正或软件重采样的方法保证采集的样本长度满足信号频率的整数倍[16],硬件的方式当转速变化率较大时容易存在误差,直接利用软件的方式难以获取到准确的基准转速信号。本文提出了一种基于软硬件结合的自动修正方法:对跟踪采样得到的信号,先自适应搜索某高频特征频率(谱号),利用其搜索值对跟踪采样点数进行修正,以消除跟踪不准、参数不精、轮径偏差、打滑等综合影响因素对实际跟踪采样点数的影响,然后重新进行傅里叶变换实现整周期化。本文主要是利用滚子通过外环应力所致振动信号实现保持架的故障诊断,因此信号中必需要含有外环特征频率,即传感器是否可接收检测滚子通过外环应力信号是首需条件。
2.1 整周期实现步骤
实现整周期主要是利用软硬件结合的方法,所谓硬件是指信号采样的方式是转速跟踪采样,由于实际轴承运转过程中,存在轴承参数、轮径参数有误差、轴承运转打滑等随机因素,因此,本文进一步提出软件修正的方式,达到修正转速跟踪采样点数的目的,具体步骤如下
步骤1 以转速跟踪采样点数I获取含有滚子通过外环应力所致的原始振动信号x(t),采样长度为N0点;
步骤2 样本筛选,即筛选振动信号的频谱中含有外环谱号的信号样本,以确保所分析信号中含有滚子通过外环应力的相关信息;
步骤3 计算/修正等效跟踪采样点数In,即在频谱的理论外环谱号P左右一定范围内(3根谱线)搜索峰值对应的谱号PW,则In=P×I/Pw;
其中理论外环谱号P可根据公式计算:
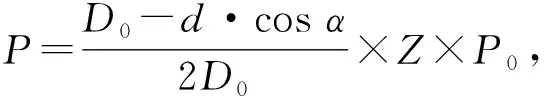
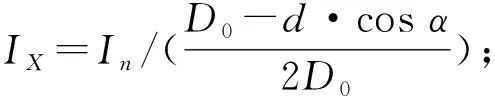
硕士研究生英语课程的设置目标,更应该着力于提高研究生的实际语言运用能力,并且要在教学上加强语言实践性[6]。语言类课程的学习有其自身的特点与规律,要区别于其他课程的学习。因此,英语课程的设置必须按照正确的语言学习规律进行。改变目前纯粹以授课型课程为主的课程安排,构建适合本学科的英语课程体系;在课程安排上不仅可以开设听力、口语、写作等传统的基础型课程,还可开设英语国家文学选读、报刊选读、西方影视文化等语言文化类课程。学校可依据现有师资力量和教学资源,为学生开设尽可能多样化的英语课程,以提高学生的英语应用水平。
步骤5 整周期化,即保持架的最大整周期数C=fix(N0/IX),则整周期化后的信号为xb(t)=x(1:round(C×N0)),其中fix表示向正方向取整,round表示四舍五入。
2.2 整周期时域回归实现保持架故障诊断
本文所述识别保持故障诊断的主要流程如图4所示,其中按保外整周期化按2.1所述步骤进行,频域滤波的主要过程是,保留滚子通过外环应力信号对应谱号P、谱号P左右1阶保外谱号Pb(Pb=P/Z)进行频域滤波(即保留谱号P、P-Pb和P+Pb),其理论依据是:正常情况下,轴承中所有滚子按固定频率等间距(允许间隔范围内)通过承载区,其频谱特征即表现为外环频率,当某个滚子间隔出现异常时,会产生频率调制(相位抖动),调制频率即为保持架公转频率,主要表现信息为左右1阶保外谱号Pb,故保留谱号P、P-Pb和P+Pb等同于提取各滚子通过承载区间距变化特征信息,对于早期微弱信号,可以将保留外环频率的所有保外边频,建议最多边频的阶数为滚子个数减1,否则延伸至了外环2阶谱号处。
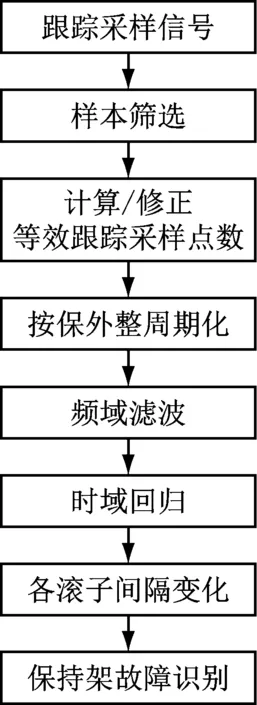
图4 本文方法主要流程
时域回归是指对原始待分析信号进行按保留最大整周期数截断处理后,利用频域滤波,对频谱结构进行处理后(如保留外环谱号P及其左右1阶保外谱号Pb)利用逆傅里叶变换(相位信息保留不变)得到经过处理后的时域信号xe(t),即时域回归后信号,达到提取或消除噪声信号的目的。
各滚子间隔变化的计算原理是:根据轴承中径D0及滚子数Z可计算出相邻2滚子理论间隔m=π×D0/Z,计算时域回归后信号xe(t)的所有极大值点对应的样本序列号PS(n)(n的总长度等于保持架最大整周期数C乘滚子数Z),各极值点产生的时刻可近似为保持架中各滚子通过检测点的采样点序号,再根据跟踪采样点数以及轴承参数,可转换为长度单位的相应各滚子间隔变化L(n)(单位为mm)。
3 仿真与应用实例分析
3.1 仿真分析
利用有限元仿真软件ABAQUS模拟保持架存在轻微磨损约1 mm的故障,如图5所示:轴承为圆柱滚子轴承,外环固定、内环旋转,内环处施加径向向下的载荷,转速跟踪采样点数I=400点/转,采样长度N0=8 000,即旋转圈数P0=20圈,模型中轴承中径D0=227 mm、滚子数Z=15、滚子直径d=34 mm、接触角α=0,正常滚子与窗梁左右允许间隙为0.5 mm,共1 mm。

图5 仿真保持架故障模型
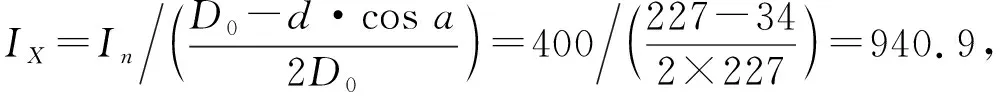
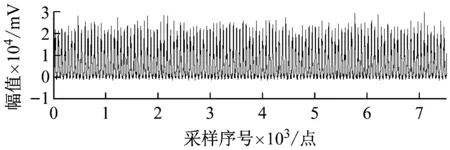
图7 整周期化后信号
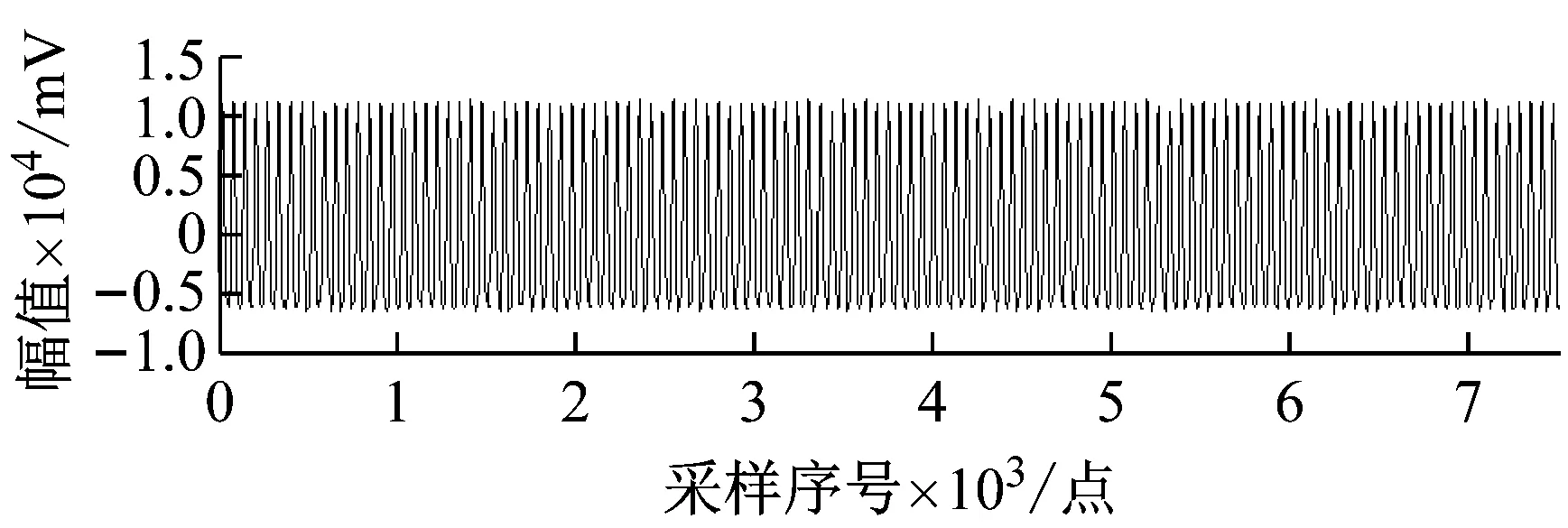
图8 时域回归后信号
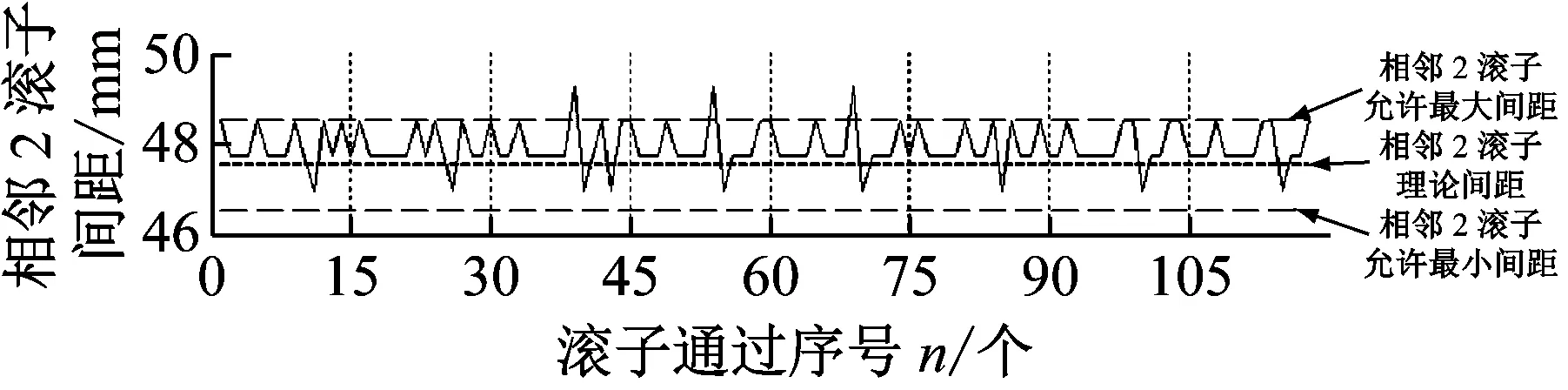
图9 各滚子间距变化
3.2 实验台数据分析
为了进一步验证实际的塑钢保持架故障诊断效果,进行了实际信号的验证。实验装置为专用的轴承实验台,通过交流电机带动旋转,由液压装置驱动轴承的轴承支座进行径向加载,如图10所示,轴承座上在承载区安装有高灵敏度振动冲击复合传感器和转速传感器进行转速跟踪采样,同步采集获取的振动冲击信号x(t),转速跟踪采样点数I=800点/转,采样长度N0=16 000,即旋转圈数P0=20圈,模型中轴承中径D0=226、滚子数Z=17、滚子直径d=34 mm、接触角α=0,故障模拟采用人工切除一个窗梁,17个滚子全部正常放入,以此来验证本文方法对滚子间距识别的有效性。

图10 轴承实验台
根据本文方法进行分析,根据相关参数,整周期化方法截取后信号长度为15 066点,得到的时域回归后信号xe(t)及相应各滚子间隔变化L(n)结果分别如图11和图12所示。从各滚子间隔变化可以发现,存在较大波动,根据相关参数相邻2滚子理论间隔m=π×226/17=41.8 mm,按正常允许1 mm间隙计算,在图中用虚线表示,如果分析出的L(n)中存在超过图中上下虚线范围内的值,则说明滚子间距异常,存在保持架故障。可以发现,图12中每个保持架周期中都存在超过最小允许间距的值,达到37 mm,比最小允许间距40.8 mm小约4 mm,可确定存在窗梁严重磨损,甚至断裂故障,磨损量约为4 mm,与实际一个窗梁的厚度相当,进一步说明了本文方法的有效性。
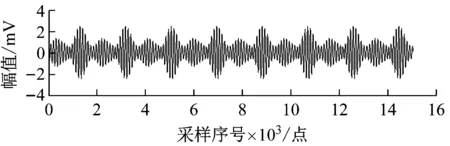
图11 时域回归后信号
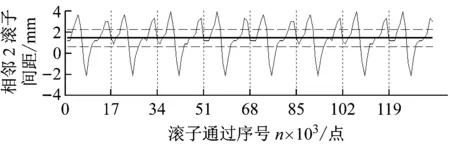
图12 各滚子间距变化
4 结 论
(1) 提出了一种可以实现非金属保持架的故障诊断新方法,基于整周期时域回归识别滚子间距变化的保持架故障诊断方法。
(2) 通过仿真和实际非金属保持架轴承试验分析,本方法能够有效提取到反映各滚子间隔是否异常的信息,从而实现保持架的故障诊断。
(3) 本方法不仅适用非金属保持架,也同样适用于金属保持架,因为分析与信号量值大小无关,故无需校对的前提下就可以实现故障的定性和定量。
(4) 本方法有二个应用前提:一是传感器必需能够敏感反应各滚子通过外环的应力变化,二是频域保留的外环对应的保外边频数不能受其他噪声影响,本文采用的整周期截取方法,能够部分解决噪声的影响。
