ARIMA-灰色耦合模型下区域医疗卫生资源供给预测*

南京医科大学健康江苏研究院(211166) 薛 宇 王长青

医药卫生事业关系亿万人民的健康，关系千家万户的幸福，是重大的民生问题。新时期医疗卫生体制改革经过近10年的探索与实践，取得了系列成果及较明确的改革思路与方向。现在是改革“深水区”，“攻坚期”迈出加速闯关克难的关键步，医联体、医共体、双向转诊、家庭签约医生、取消药品加成、医保异地结算、远程医疗、智慧医院、互联网+医疗健康等一系列改革组合拳，为解决“看病难”、“看病贵”集中发力。当然医疗卫生体制改革有个前提，就是医疗卫生资源供给总量问题，如果医疗卫生资源供给不足，或无法准确预测未来的医疗卫生资源供给问题，再好的改革方案也无法实施。特别是卫生人力资源的行业特殊性，有培养周期和人员配置问题。所以我们要了解和预测未来10年或更长时间有多少医疗人才资源、医疗床位数等卫生资源供给市场，再根据需求调整改革方向，调整卫生人才培养计划，真正解决看病难问题。为了相对准确预测区域规划年医疗卫生资源供给总量，本文在ARIMA预测模型(autoregressive integrated moving average model,ARIMA)及灰色预测模型基础上，建立ARIMA-灰色耦合预测模型，并通过实证分析预测区域医疗卫生资源供给，从而为医疗卫生体制改革提供数据支持。

预测模型选择

近年来学术界积累了许多对医疗卫生资源预测的方法[1-10]，但多数还是运用单一的预测方法。而医疗卫生资源的供给受多种因素影响，资源本身又是个系统，包含多种内容与形式，每种资源的特点都不同。考虑到卫生资源的供给变量为时间序列变量，本文提出运用组合模型进行预测。预测模型的选择需考虑预测对象的特点，以及模型的适应范围。

从医疗卫生资源时间序列的特点看，首先我国卫生事业发展过程中，进行过四次医疗卫生体制改革，所以近年来卫生事业行业出台政策较多，这直接影响到医疗卫生资源在时间序列上发展不稳定，无论是医疗床位，还是医疗卫生人员作为变量，其时间序列发展规律不明显；其次因为是按阶段改革，所以在时间轴上，医疗卫生资源有效序列多为短序列；第三在预测医疗卫生资源供给时，多进行5～10年内的预测，属于短中期预测。

从预测模型的适应性看，通过查阅文献，灰色预测模型适应于不稳定或无规律性的或样本少的数据，预测准确度相对较高，已广泛用于社会经济等方面的预测，成为较成熟的预测工具。而ARIMA预测模型，将预测对象随时间推移而形成的数据序列视为一个随机序列，用一定的数学模型来近似描述这个序列，这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值，在时间序列样本预测中应用广泛。

结合上述分析，考虑到ARIMA模型、灰色预测模型的特征与预测条件，以及卫生资源供给与需求的时间序列特点，本文引入ARIMA-灰色耦合模型预测区域医疗卫生资源的供给。

在开展ARIMA模型、灰色预测模型、ARIMA-灰色耦合模型对医疗卫生资源供给预测时，主要以医疗床位数和注册医生数作为供给两个主要指标。资源选取区域近15年或20年医疗床位总数和注册医生总数，建立指标时间序列数据，数据来源于区域卫生年鉴和统计年鉴。

构建ARIMA-灰色耦合模型

耦合预测模型主要是通过选取两种或两种以上预测模型，分别进行预测，然后通过预测结果，建立耦合关系，确定耦合权重，从而测算耦合后的预测值。ARIMA-灰色耦合模型就是先进行ARIMA模型预测和灰色模型预测，通过两个预测模型预测结果的误差大小，建立耦合关系，计算耦合权重，从而测算出耦合后的预测值。ARIMA-灰色耦合模型本质上是一种组合模型，目的是减少系统误差。其原理如图1。

图1 耦合预测模型原理

设f1为ARIMA预测值，f2为灰色模型预测值，f3为耦合预测值，三种方法的预测误差分别为e1、e2和e3，取w1与w2分别为ARIMA和灰色模型预测的权重，且w1+w2=1，则得

f3=w1f1+w2f2

(1)

(2)

实例分析

江苏省医疗卫生资源供给预测主要是预测江苏省规划年(2025年)医疗床位数供给总量与注册医生数供给总量。

1.医疗床位数预测

(1)ARIMA预测

第一步：数据预处理

选取江苏省2000-2014年医疗床位数，组成时间序列HB(hospital bed)，如表1，绘制时间序列图2。运用Eviews 8.0进行分析。

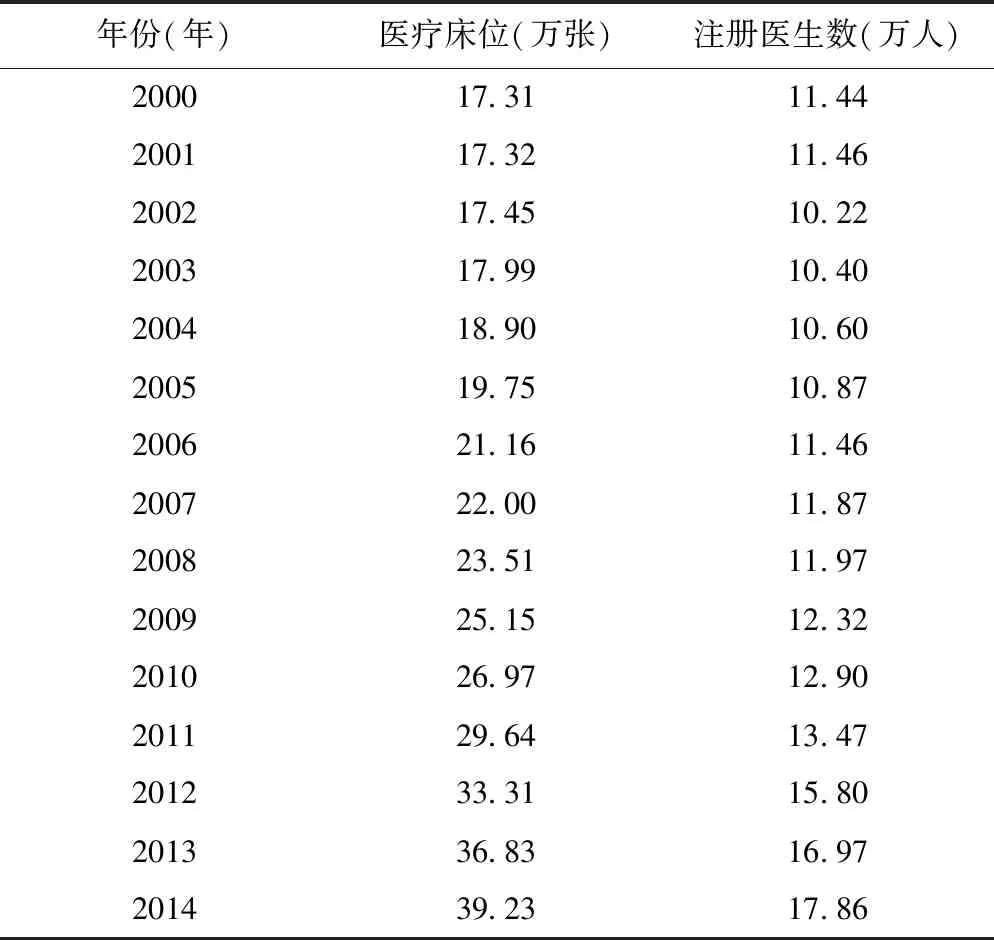
表1 江苏省医疗床位数与医生数历史数据表

*：数据来源：《2015年江苏卫生年鉴》、《2015年江苏统计年鉴》

可以明显看出序列HB是非平稳序列，为消除趋势同时减少序列的波动，对序列数据取对数，令X=lnHB，并且进行一阶差分，记Z=ΔX，Δ为一阶差分算子。对序列Z进行单位根检验，在10%、5%、1%的显著性水平下，通过AIC最小准则选取阶数，检验结果见表2。

表2 序列Z的ADF检验结果

可以看出序列Z为平稳的时间序列(即模型参数d=1)，可以进行模型拟合。

第二步：最优模型判定

通过上述分析，这里选用ARIMA(p,d,q)模型，其中d=1，p是自回归的阶数，q是移动平均的阶数，通过对Z序列的自相关和偏相关图(图2)的观察，可以获得p与q的值，分别是p=1，q=0。

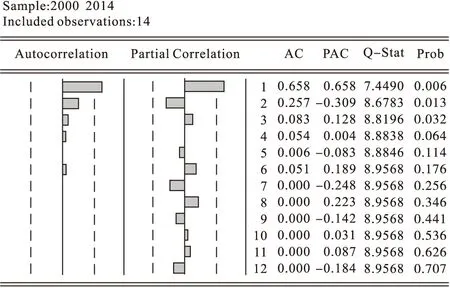
图2 自相关与偏相关图

根据AIC原则，选择ARIMA(1,1,0)模型。

第三步：模型检验

根据上述所建模型，得到实际值与预测值之差即残差。对残差进行自相关与偏自相关分析图可知，系数的检验t=-23.06925，P<0.05，自相关系数都很小，在置信水平为95%的置信区间。进行白噪声检验过程中，所有的P均大于0.05，故残差序列是一个白噪声过程，说明建立的模型ARIMA(1,1,0)是可行的。

第四步：预测

依据ARIMA(1,1,0)模型，序列HB的预测模型表达式可以写为：

(1-0.982605B)(1-B)log(HB)=εt

将上式做反对数变换可得到规划年床位数预测结果，从实际值与预测值结果的残差可以看出，残差多为大于零，预测值总体偏小于实际值。结果如表3。

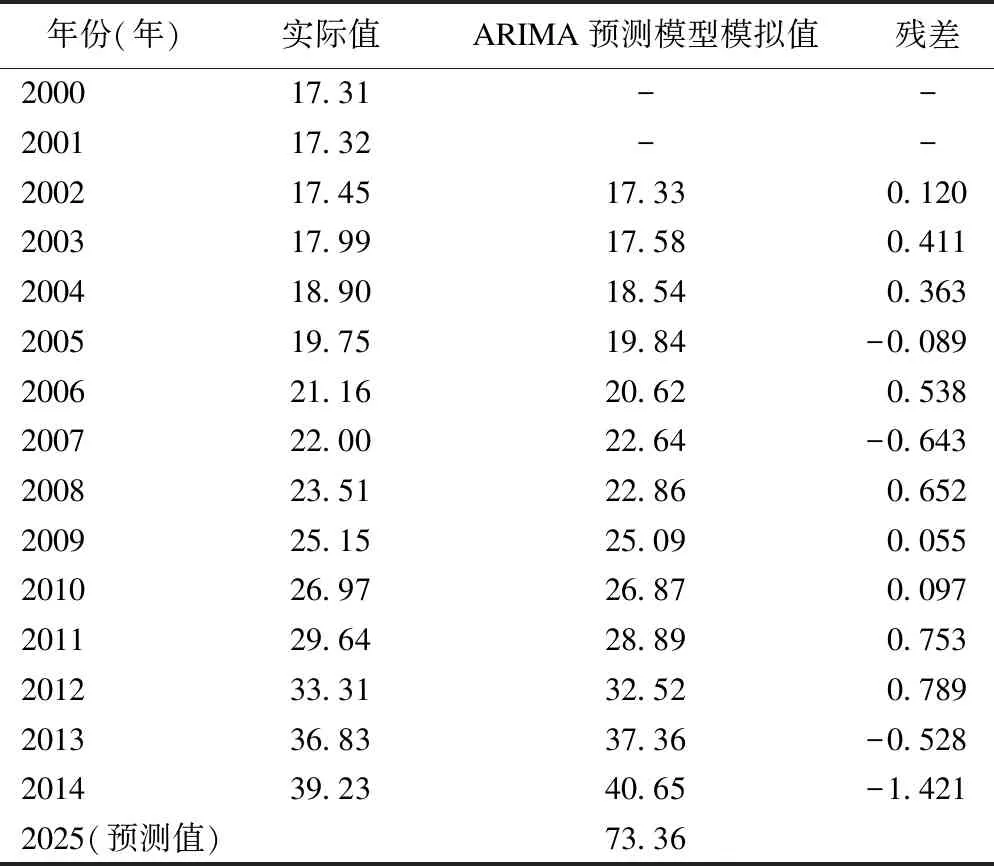
表3 江苏省医疗床位数ARIMA预测模型预测值(万张)

(2)灰色模型预测

建立2000-2014年医疗床位数时间序列的原始序列如下：

X(0)=(17.31,17.32,17.45,17.99,18.90,19.75,21.16,22.00,23.51,25.15,26.97,29.64,33.31,36.83,39.23)

生成累加序列：

X(1)=(17.31,34.63,52.08,70.07,88.97,108.72,129.88,151.88,175.39,200.54,227.51,257.15,290.46,327.29,366.52)

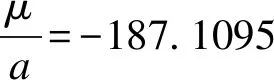
根据上述分析写出床位数灰色预测模型GM(1.1)的表达式：

对上述预测模型进行精度检验：后验差比值C=0.02834112，小误差概率P=1，表示预测精度的等级好。经过检验，模型在医疗床位预测中精度较高，可以用于预测江苏省规划年医疗床位数。从表4可以看出，从实际值与预测值结果的残差可以看出，残差多为小于零，拟合值总体偏大于实际值。

(3)ARIMA-灰色耦合预测

根据上文ARIMA预测残差与灰色模型预测残差，计算两者残差的方差，根据公式(1)、(2)，可求出江苏省2025年床位数耦合预测结果如表5。

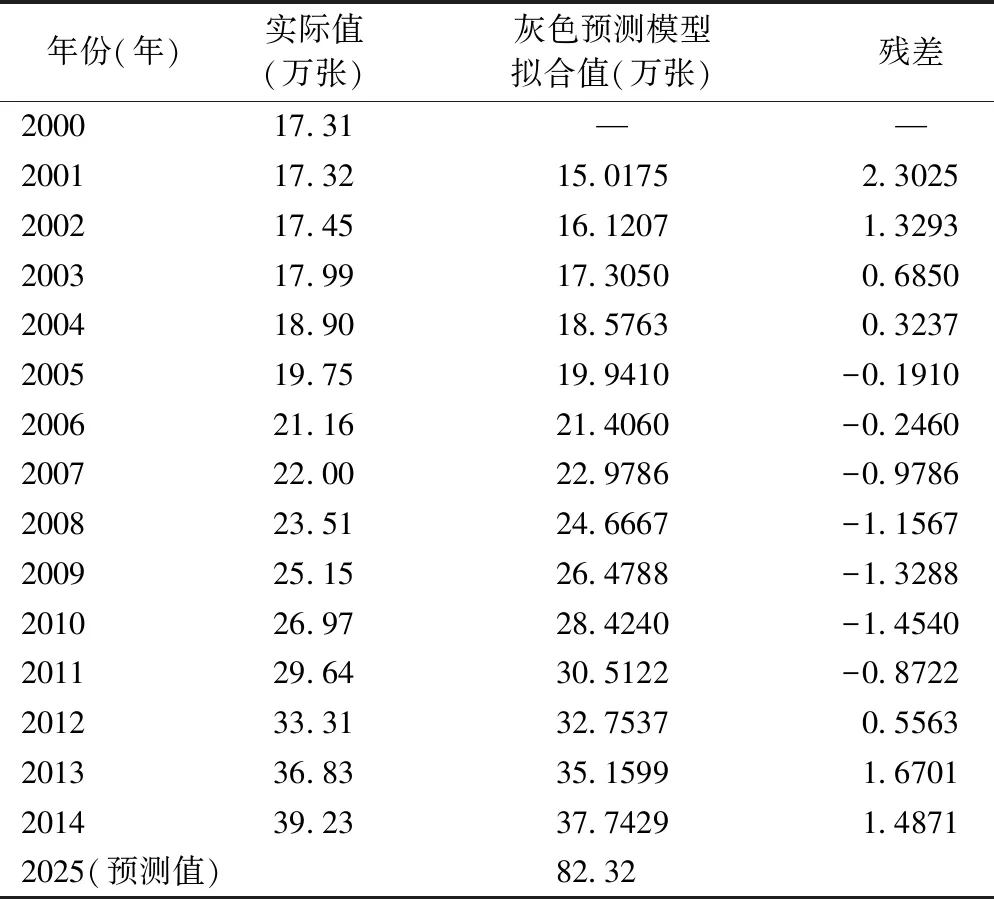
表4 江苏省医疗床位数灰色预测模型预测结果

表5 2025年医疗床位数预测值(万张)

根据ARIMA预测模型进行预测，从实际值与拟合值结果的残差可以看出，残差多为大于零，拟合值总体偏小于实际值。根据灰色预测模型预测结果看，实际值与拟合值结果的残差多小于零，拟合值总体偏大于实际值。对于规划年的预测，两种预测结果分别是73.36万张、82.32万张，两个结果相差较大，分别偏离“实际值”两边，而ARIMA-灰色耦合预测模型的预测结果为77.65万张，介于ARIMA预测模型与灰色预测模型的预测结果之间，是较科学的预测结果。

2.注册医生数预测

(1)ARIMA预测

第一步：数据预处理

江苏省2000-2014年注册医生数，组成时间序列RD(registered doctor)，如表1，绘制时间序列图。运用Eviews 8.0进行分析。

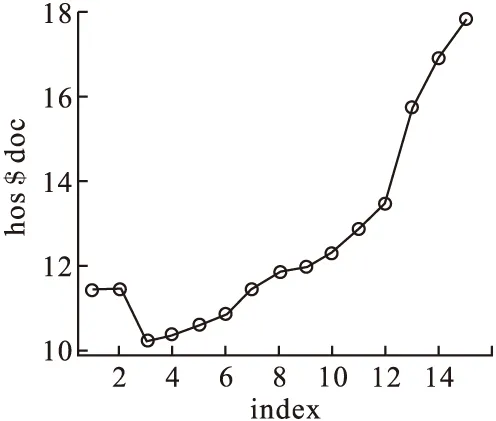
图3 序列RD的时序图

从图3可以明显看出序列RD是非平稳序列，为消除趋势同时减少序列的波动，对序列数据取对数，令X=lnRD，并且进行二阶差分，记Z=Δ2X，Δ2为二阶差分算子。对序列Z进行单位根检验，在10%、5%、1%的显著性水平下，通过AIC最小准则选取阶数，检验结果见表6。

表6 序列Z的ADF检验结果

可以看出序列Z为平稳的时间序列(即模型参数d=2)，可以进行模型拟合。

第二步：最优模型判定

通过上述分析，这里选用ARIMA(p,d,q)模型，其中d=2，p是自回归的阶数，q是移动平均的阶数，通过对Z序列的自相关和偏相关图(图略)的观察，可以获得p与q的值，分别是p=0，q=1。根据AIC准侧，选择ARIMA(0,2,1)模型，其表达形式为：

(1-B)2log(HB)=(1+0.631123B)ε1

第三步：模型检验

根据上述所建模型，得到实际值与预测值之差即残差。对残差进行自相关与偏自相关分析可知，P<0.05，自相关系数都很小，在置信水平为95%的置信区间。同时该残差序列是一个白噪声过程，说明建立模型ARIMA(0,2,1)是合适的。

第四步：预测

依据ARIMA(0,2,1)模型，因为Z=ΔX=ΔlnRD，所以序列RD的预测模型表达式可以写为：

(1-B)2log(HB)=(1+0.631123B)εt

将上式做反对数变换可得到规划年注册医生数预测结果。结果如表7。

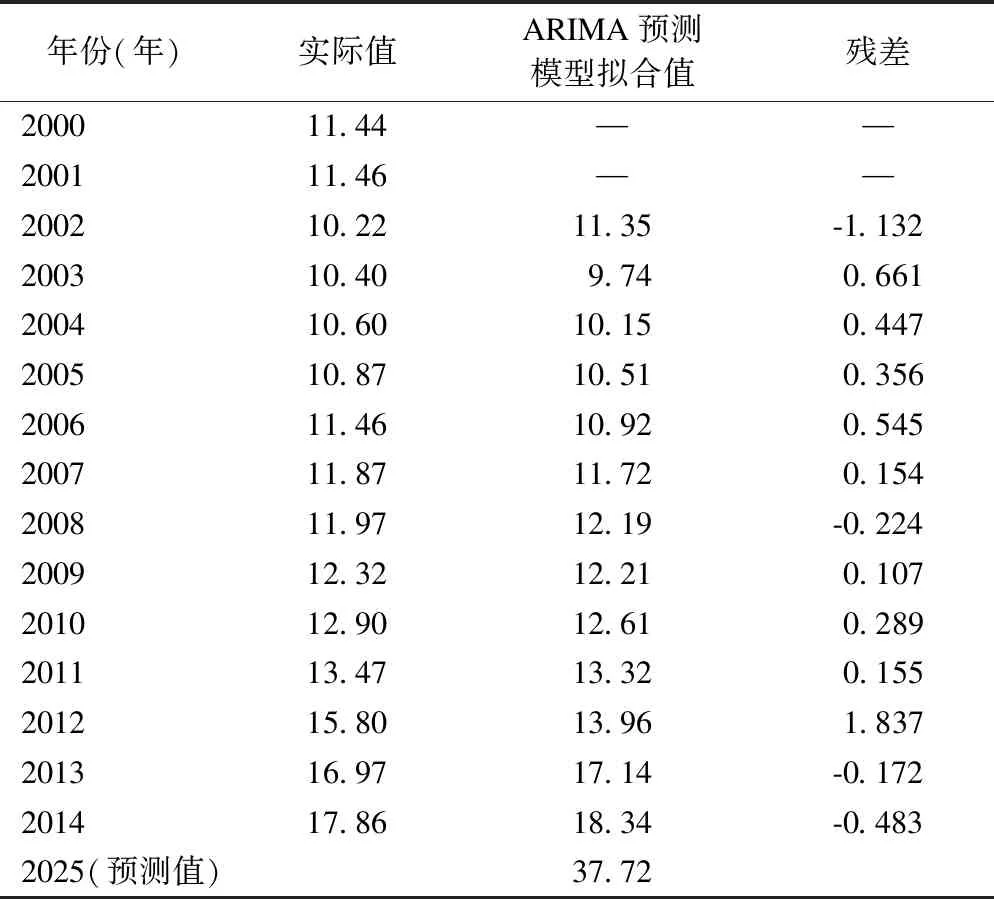
表7 江苏省注册医生数ARIMA预测模型预测值(万人)

(2)灰色模型预测

建立2000-2014年注册医生数时间序列的原始序列如下：

X(0)=(11.44,11.46,10.22,10.40,10.60,10.87,11.46,11.87,11.97,12.32,12.90,13.47,15.80,16.97,17.86)

生成累加序列：

X(1)=(11.44,22.90,33.12,43.52,54.12,64.99,76.45,88.361,100.29,112.61,125.51,138.98,154.78,171.75,189.61)

最终得出注册医生数灰色预测模型GM(1.1)的表达式：

经过检验，模型在注册医生预测中精度较高，可以用于预测江苏省规划年注册医生数。用模型预测江苏省2025年注册医生数如表8。

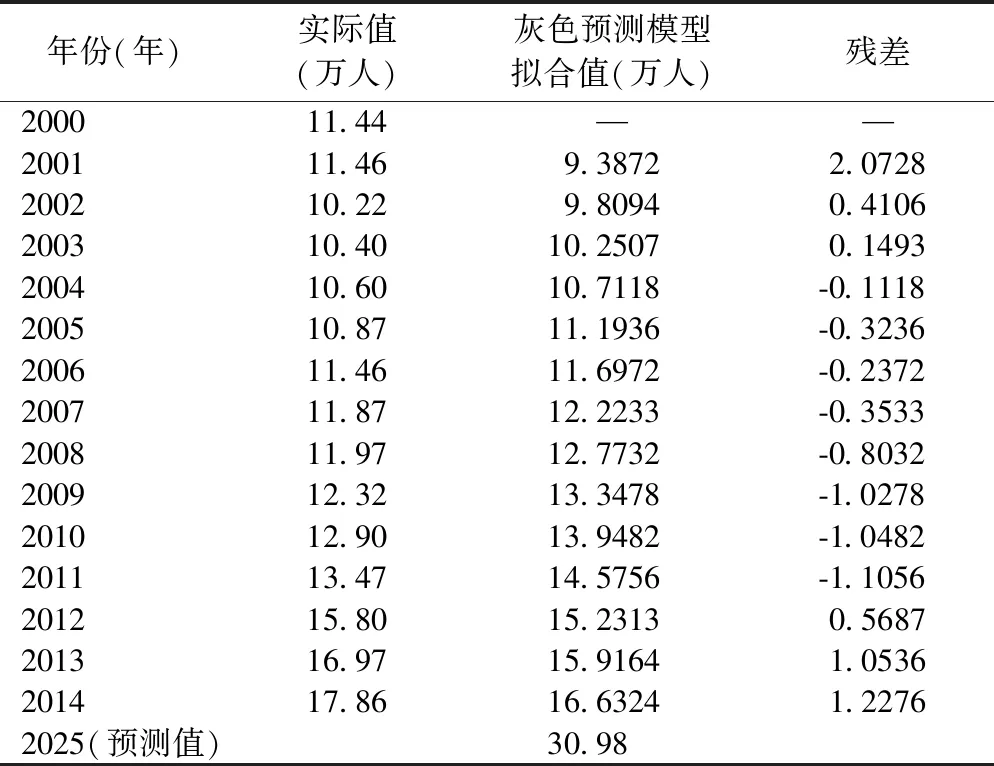
表8 江苏省注册医生数灰色预测模型预测结果

(3)ARIMA-灰色耦合预测

根据ARIMA预测残差与灰色模型预测残差，计算两者残差的方差，根据公式(1)、(2)，可求出江苏省2025年注册医生数耦合预测结果如表9。

表9 2025年注册医生数预测值(万人)

在注册医生的预测中，根据ARIMA预测模型进行预测，从实际值与拟合值结果的残差可以看出，残差多为小于零，拟合值总体偏大于实际值。根据灰色预测模型预测结果看，实际值与拟合值结果的残差多大于零，拟合值总体偏小于实际值。对于规划年的预测，两种预测结果分别是37.78万人、30.98万人，两个结果相差较大，分别偏离“实际值”两边，而ARIMA-灰色耦合预测模型的预测结果为34.49万人，介于ARIMA预测模型与灰色预测模型的预测结果之间，也是较科学的预测结果。

结 论

ARIMA预测模型需要时间序列数据必须是稳定的，如果不稳定的数据，是无法捕捉到规律的，如果时间序列稳定就比较适合预测近期与中期。而灰色预测模型需要的数据量比较少，预测比较准确，精度较高，样本分布不需要有规律性，计算简便，检验方便，灰色预测模型适用于中长期预测。对于医疗卫生资源中的床位数与医生数，从时间序列来看，是随时间增长而增长，虽然是呈线性，只体现上升趋势，线性残差较大。对于预测2025年这个规划年数据，两种预测模型都存在不足。而通过ARIMA-灰色耦合预测模型，通过实证分析，很好地解决了ARIMA预测中离散特性以及灰色预测模型的收敛特性，使得预测结果相对两种单独预测的模型更加科学。

从实证分析的结果看，预计江苏省医疗床位数与医生数在2025年分别达到77.65万张、37.78万人，分别是2014年的1.97倍、2.11倍，2017年的1.66倍、1.67倍，比2017年的床位数与医生数分别多37.5万张、13.59万人，2017年至2025年还有8年时间，每年需要递增床位数与医生数分别是4.68万张、1.70万人，这为江苏省医疗卫生区域规划、医疗卫生资源配置、医疗人才培养、医学生招生计划设置提供了科学参考。