通信服务行业寡头博弈分析

宁乃聪

(天津大学 管理与经济学部，天津 300072)

21世纪以来，互联网技术的飞速发展刺激了经济的增长，据国家统计局的资料显示，我国互联网使用人数近十年来超速增长，截至2017年，我国互联网使用人数增长近3倍。5G时代的到来及虚拟运营商的发展对电信运营商提出了越来越高的要求。而目前通信行业存在三大问题，第一是通信服务现状有待提高，如基层存在乱收费问题，部分地区信号流畅性差，公司推出的产品用户友好性不强等；第二是人才队伍不足；第三是缺乏创新。李恩平[1]提出通信行业应树立正确的思想观念，全面提升服务质量，从而提高行业竞争力。RAJASEKAR等[2]利用波特五力模型分析了阿曼国的电信行业，并且指出客户的购买与使用决定是由价格、价值和服务质量共同决定的。THAICHON等[3]对泰国的通信市场进行调研，将数据供应商的服务质量分为网络质量、客户服务与技术支持、信息质量、安全和隐私4个部分，同样将顾客的使用习惯进行市场划分，最后检验了网络数据提供商服务质量和顾客感知价值、信任和承诺之间的关系。BELWAL等[4]运用了SERVQUAL模型，分析了Oman国家的电信双寡头企业，提出了服务质量的可靠性和保障性可以提高寡头企业的长期利润和顾客的忠诚度。QUACH等[5]提出了通信行业的服务质量矩阵，并进一步研究了服务质量矩阵在高科技领域对于顾客忠诚度的影响。

自移动通信业务在我国正式推出以来，我国的电信市场一直属于寡头垄断的地位，在供给侧改革与移动数据市场改革的背景条件下，各个运营商均响应政府的号召，不断进行改革创新，提高自身服务业务水平。通信行业寡头垄断方面，王若冰[6]对我国电信行业的市场行为做了分析，指出我国电信行业发展的4个阶段且目前正处于寡头垄断阶段，建立了寡头博弈模型并进行了均衡解分析。何曼[7]分析了中国通信市场上的两大寡头移动与联通之间的博弈行为，建立了静态伯川德博弈模型和基于卡尔特的博弈分析，指出了行业存在的问题，并提出两大运营商只有进行合作，实施差异化战略才能充分发挥通信网络的整体效能。肖浩芳等[8]建立了一个基于古诺模型的移动数据定价策略模型，计算得出均衡解，并在均衡解的条件下讨论出几种新的定价模式，如水电行业的阶梯定价法和博弈论定价法。马文静等[9]考虑了通信行业基于古诺模型和斯坦尔伯格模型的寡头博弈，提到不完全信息的竞争导致了纳什均衡的出现，并指出寡头垄断带来服务质量低下等弊端。XU等[10]研究了无线通信市场的动态博弈状况，指出了在理想情况下，数据供应商可以通过提供不同类型的服务组合从而获得更多的利润。杨世旭等[11]从产品、价格与服务3个维度建立了电信行业寡头的动态模型，分析了3家运营商的博弈特点与运营策略，指出了在新的挑战下，3家运营商应放弃价格战，不断开发新的业务，提高服务质量，才能发挥通信网络的整体效能。CHEN等[12]通过建立Bertrand模型和有限理性模型，对中国通信行业市场的寡头博弈进行研究，得出了纳什均衡点并进行数值模拟分析，探讨了其稳定性。陈远高等[13]分析了一个Stackelberg博弈的双渠道的供应链问题，重点研究了定价和服务水平两大问题，通过进行数值分析，得出服务的横向合作可以提高供应链的利润。陈正义等[14]建立了通信行业随机需求的条件下寡头的价格策略模型，仿真了系统的动态演化过程，指出微分价格博弈模型存在唯一的鞍点均衡路径。

综上可知，以往的研究主要结合博弈论，对通信寡头企业建立产量或者价格模型，之后进行均衡解求解与复杂性分析。在各公司市场份额趋于稳定的今天，服务质量越来越作为通信公司的主要竞争变量，服务质量包括信号覆盖率、网络速率、基层人工服务、新产品的便捷性等。因此，笔者主要针对服务质量对寡头博弈带来的影响，假设市场中存在两个博弈方，通过建立服务差异化的寡头模型和随机需求的引入，对均衡解下的最优服务水平进行了相关参数的研究，分析寡头企业服务水平对系统演化的影响，并给出了相关性的建议。

1 模型建立

通信行业背景下，寡头垄断带来了很多弊端，如资费价格高，服务态度差等。随着国家改革及创新力度的不断加大，通信寡头企业不断调整自身的行为，提高自身服务质量与业务水平，响应政府号召，加大改革力度。以往研究表明，电信服务水平对顾客购买使用、忠诚度及公司的行业竞争力和利润都有较大影响，与传统方法中将价格或产量作为企业决策变量不同的是，笔者将服务质量作为模型的决策变量，服务质量分别是价格与产量的函数，模型中涉及到的主要参数如表1所示。

笔者讨论一个基于服务质量竞争的双寡头模型的公司，分别为公司1和公司2。模型部分假设公司1目前的市场占比为o，公司2目前的市场占比为1-o。公司的成本主要考虑变动成本，其由两部分组成，第一部分为数据流量的单位变动成本c；第二部分为服务质量变动引发的成本v×c×si，即是通信公司通过增强人员素质、新增基础建设及加强科技创新而带来的服务质量变动成本,其中v为服务成本系数。z1为掠夺系数，是通信公司通过提高自身服务业务水平从对方市场掠夺客户引发的系数，也可理解为公司渴望竞争的系数，该模型中公司1掠夺的市场份额为z1(s1-s2)，公司2掠夺的市场份额为z1(s2-s1)，若公司1为增益，则公司2为损失。z2为市场增加系数，即两个公司通过提高自身服务从而带来更多的客户与数据使用量的增加。通信公司服务质量的提高包括数据附加产品的便捷性、更好的人工服务及更高的通信网络覆盖率等，服务质量的提高可以带来更好的客户满意度，从而带来更多的数据流量使用及主动消费。对于公司1而言，市场规模的增加为z2s1，对于公司2而言，市场规模的增加为z2s2。笔者研究通信行业的一个双寡头公司模型，假设通信公司提供的数据产品是同质的。

表1 模型参数

通信公司的移动数据定价P为:

P=a-b(q+z2(s1+s2))

(1)

通信公司的单位成本C为：

C=cvsi+c

(2)

通信公司的单位利润Pu为：

Pu=a-b(q+z2(s1+s2))-cvsi-c

(3)

通信公司1的市场需求D1为：

D1=oq+z1(s1-s2)+z2s1

(4)

通信公司2的市场需求D2为：

D2=(1-o)q+z1(s2-s1)+z2s2

(5)

通信公司1的利润为：

Profit1=(a-b(q+z2(s1+s2))-

cvs1-c)(oq+z1(s1-s2)+z2s1)

(6)

通信公司2的利润为：

Profit2=(a-b(q+z2(s1+s2))-

cvs2-c)((1-o)q+z1(s2-s1)+z2s2)

(7)

2 纳什静态均衡解分析

对于两个寡头公司而言，假设同时作出决策。服务质量作为寡头企业的决策变量，为了方便求得均衡解，首先让利润分别对各自的服务水平求解偏导得到两公司的边际利润。

公司1的边际利润为：

(c+cvs1-a+b(q+z2(s1+s2)))-

(cv+bz2)(oq+s1z2+z1(s1-s2))

(8)

公司2的边际利润为：

s2z2+q(o-1))-(z1+z2)·

(c+cvs2-a+b(q+z2(s1+s2)))

(9)

(10)

(11)

为了对纳什静态均衡解作出分析，首先取最优服务水平的差值来分析市场占比o、服务成本系数v和掠夺系数z1对最优服务水平的影响。

(12)

服务成本系数是服务水平影响成本的直接变量，对服务水平的差值求关于服务成本系数的导数，来探究最优解差值和服务成本系数v的关系：

(13)

通过得到的微分可以发现，市场占比的大小将直接影响服务水平差值的斜率。

(1)当o=0.5时，两公司的最优服务水平无差异。

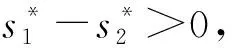
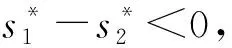
为了对上述关系给出更为直观的表达，取参数a=10，c=1，b=1，z1=1.5，z2=1.8，q=1，并分别对上述3种情况进行数值模拟与仿真。市场占比o、服务成本系数v和服务水平差值三者的关系如图1所示，可知不论两企业的市场占比如何，服务成本系数的增大均会不断地缩小最优服务水平的差值。当o=0.4时服务成本系数与服务水平差值的截面图如图2所示，可知随着服务成本系数的增大，服务水平差值逐渐减小。双寡头企业市场占比相同且o=0.5时服务成本系数与服务水平差值的截面图如图3所示，可知随着服务成本系数的变化，服务水平的差值始终保持不变。o=0.6时服务成本系数与服务水平差值的截面图如图4所示，可知随着服务成本系数的增大，服务水平差值依然逐渐趋近于0。综上可知，随着成本系数的增大，两公司的服务水平更为接近，从而降低掠夺项的大小，避免了企业的无序竞争。

图2 服务成本系数与服务水平差值的关系(o=0.4)

图3 服务成本系数与服务水平差值的关系(o=0.5)

图4 服务成本系数与服务水平差值的关系(o=0.6)

掠夺强度也是笔者探讨的重要内容，接下来分析最优服务水平差值与掠夺系数z1的关系，首先对服务水平差值求关于掠夺系数的导数：

(14)

由式(14)可知，掠夺系数项同样需分3种情况来讨论。

(1)当o=0.5时，两公司的最优服务水平无差异。

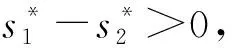
为了更好地对上述关系进行表达，取参数a=10，c=1，b=1，z2=1.8，q=1，v=0.5，对上述方程进行数值模拟与可视化表达。市场占比o、掠夺系数z1和服务水平差值三者的关系图如图5所示。图5的截面图如图6所示，取了多项市场占比系数进行更为直观的表达，可知除了o取0.5时差值不变以外，其余情况下掠夺系数的增大均会使服务水平差值不断趋近于0。这与实际情况也较为吻合，随着竞争激烈程度的加剧，企业之间彼此追赶与学习，企业最优服务水平会慢慢地接近，从而寡头需要寻找新的创新与突破点以提高自身竞争力。

图5 o, z1和服务水平差值的3D图

图6 o,z1与服务差值的关系(多个截面)

3 需求不确定下的博弈分析

笔者将随机项加入需求函数中，假设随机需求系数ε1、ε2服从U(-Δ,Δ)均匀分布，根据以上模型，可以得出以下结果。

通信公司1的市场需求D1,ε为：

D1,ε=oq+z1(s1-s2)+z2s1+ε1

(15)

通信公司2的市场需求D2,ε为：

D2,ε=(1-o)q+z1(s2-s1)+z2s2+ε2

(16)

通信公司的移动数据定价Pε为：

Pε=a-b(q+z2(s1+s2)+ε1+ε2)

(17)

通信公司的单位利润Profitu,ε为：

Profitu,ε=a-b(q+z2(s1+s2)+

ε1+ε2)-cvsi-c

(18)

通信公司1的利润为：

Profit1,ε=(a-b(q+z2(s1+s2)+

ε1+ε2)-cvs1-c)×

(oq+z1(s1-s2)+z2s1+ε1)

(19)

通信公司2的利润为：

Profit2,ε=(a-b(q+z2(s1+s2)+ε1+ε2)-

cvs2-c)×((1-o)q+z1(s2-s1)+z2s2+ε2)

(20)

对于公司1而言，其期望利润为：

(-a+c+cvs1+b(q+(s1+s2)z2))+bΔ2)

(21)

对于公司2而言，其期望利润为：

4((-1+o)q+s1z1-

s2(z1+z2))(-a+c+cvs2+

(22)

(23)

(24)

上述方程求得的解与未加入随机需求变量时的解相同。由此可见，最优服务质量与随机需求无关，因此公司还要专注于服务质量的提升。

再研究需求不确定情况下掠夺系数对于公司总利润的影响，其中公司总利润的表达式为：

Total_Profitε=E(Profit1,ε)+E(Profit2,ε)=

b(q+(s1+s2)z2))+3((-1+o)q+

s1z1-s2(z1+z2))×(-a+c+cvs2+

b(q+(z2(s1+s2)))-2bΔ2)

(25)

对公司总利润求关于掠夺系数z1的导数，可以得到：

(26)

可见，掠夺系数的大小将直接影响公司均衡解下总利润的大小，且公司的总利润值随着掠夺系数的增大而减小。

4 结论

通信行业的发展使服务水平成为寡头博弈越来越受关注的对象，不同于传统方法中将价格和产量作为博弈变量，笔者创新性地将服务水平引为决策变量。基于通信行业，运用了运筹学和数值模拟仿真的方法对博弈过程中的服务均衡解做了研究，分析了服务变量在博弈过程中的变化。

通过对静态博弈的均衡解进行研究，得出了以下结论：①市场占有率小的公司会有更高的服务水平；②寡头服务水平差值的大小会随着服务成本系数及竞争激烈程度的增大而减小，且这时相应的总利润会减小；③寡头最优服务水平的差值与潜在市场规模和需求波动无关。

因此，一方面，博弈产生了竞争，市场占比产生了服务差距，故通信服务业在保持市场优势的同时也要关注自身服务水平的变化，从而多方面的增强自身优势；另一方面，没有差异化不意味着就是好事情，而服务差异化也不意味着不合作。一定的服务水平差异化有利于系统总利润的增大，因此保持市场结构，通过合作与科技创新降低成本将会使寡头企业受益。