基于滑模理论的旋翼无人机容错飞行系统研究
2019-09-17黄龙亮徐雪琴黄晓飞曹祥
文/黄龙亮 徐雪琴 黄晓飞 曹祥
1 引言
目前,中小型旋翼无人机已被广泛用地形测绘、匪徒追捕、植保、配送快递等任务,但旋翼无人机却面临对故障容忍度极低的问题,尤其是电机、桨叶等执行机构发生故障后直接导致坠机。因此如何保证旋翼机在执行机构发生故障后,仍能安全飞行或是着陆显得十分重要。针对这一问题,可以通过提高控制系统的鲁棒性能来减小故障造成的系统不稳定,提高系统的可靠性。文献[1]设计非线性轨迹控跟踪器,用观测器的观测量补偿控制器以解决执行机构有效性损失的问题,通过仿真表明其有效性;文献[2]针对执行机构故障,设计滑模控制器,借助搜索算法进行控制参数的选取,仿真比较好。文献[3]采用冗余执行机构来补偿,通过仿真完成该方法验证。除此之外,还有利用PID控制[4-6]、预测控制[7-8]等提高旋翼机的可靠飞行,但更多只是仿真而无实际飞行验证。本文针对旋翼机桨叶损坏这一执行机构故障,应用积分滑模理论,对四旋翼无人机的非线性模型设计容错控制器,以提高其飞行可靠性,通过仿真和飞行实验验证该控制器在飞行时的安全性能。
2 四旋翼无人机非线性建模
(1)四旋翼无人机质心在机架的几何中心处,电机的升力面和重心位于同一个平面上,且电机无安装误差角;
(2)四旋翼为刚体;
(3)不考虑空气阻力带来的影响;
(4)忽略桨的陀螺效应。

表1:四旋翼无人机主要参数

表2:容错控制器设计参数
根据上述假设以及无人机的运动学和动力学分析,可得到简化的四旋翼无人机数学模型[9]:
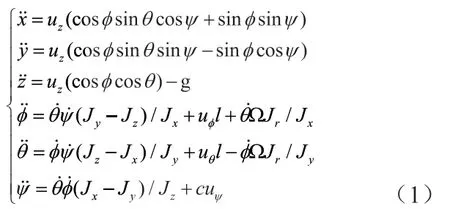
其中,Ω表示由电机引起的扰动,Ω=Ω1-Ω2+Ω3-Ω4,Ωi为电机的角速度;θ为俯仰角,为滚转角,ψ为偏航角,x、y、z分别为地面坐标系下的位置分量;Jx、Jy、Jz分别表示各个轴的转动惯量,Jr表示单个桨叶的转动惯量;c表示电机反扭矩系数d与电机转速对应的升力系数b的比值;l表示电机到飞机质心的距离;分别为俯仰、滚转、偏航和高度四个通道的输入,且有其中表示各个桨叶提供的升力。
当桨叶发生故障时,由此引起的执行机构失效是近似常数,并把执行机构失效间接转为俯仰、滚转、偏航和高度通道控制输入的损失,结合(1)式,所以状态方程可以
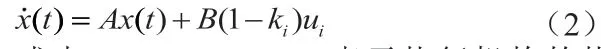
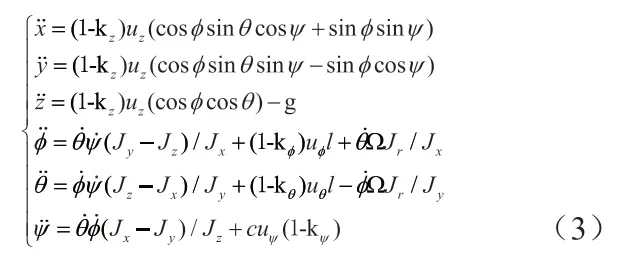
3 四旋翼无人机容错飞行控制器设计
从(3)式中看出,旋翼机桨叶损坏这一执行机构故障,会带来控制通道输入的损失,因此本论文应用积分滑模理论,对四旋翼无人机的非线性模型设计容错控制器,以提高其飞行可靠性。
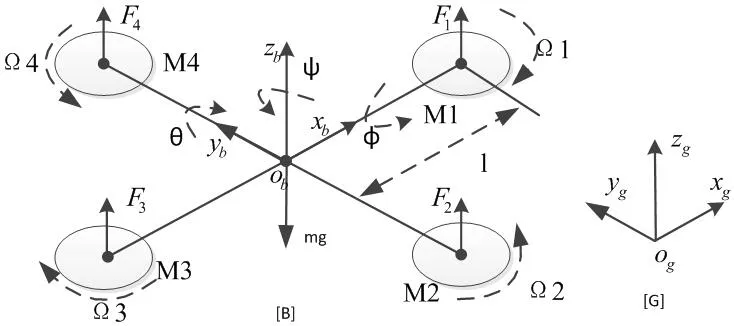
图1:四旋翼无人机原理示意图
设计的被动容错飞行控制结构如图2所示。整个控制结构分为位置控制和姿态控制两部分,其中姿态控制部分的期望的偏航角设为已知,而期望的俯仰角、滚转角需要经过位置控制得到;然后将通过姿态控制得到的通道控制量和高度通道控制量分配成四个电机的控制输入,从而完成四旋翼无人机的控制。位置控制和姿态控制选用积分滑模控制。
位置回路控制包括x、y、z的控制,姿态回路包括滚转、俯仰、偏航三通道的控制律设计,是实现定点飞行和自主飞行的关键环节,本论文在滑模面中加入跟踪量的积分项来增强滑模控制器的抗干扰能力,减小稳态误差,即设计滑模函数为
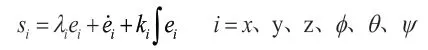
结合公式1、公式4,则有滑模函数的微分形式
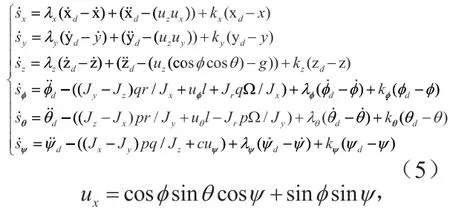
在系统的滑模控制中都伴随一定的抖振,为了减小控制过程中的抖振,用饱和函数代替理想滑动模态中的符号函数能够使得一定范围内的状态点都被吸引到滑模面的某一邻近区域内,即边界层内,δ为边界层。当时,当当则将带入公式(5)得到位置回路的控制量为
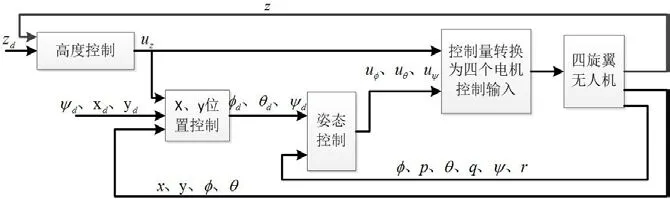
图2:容错飞行控制结构图
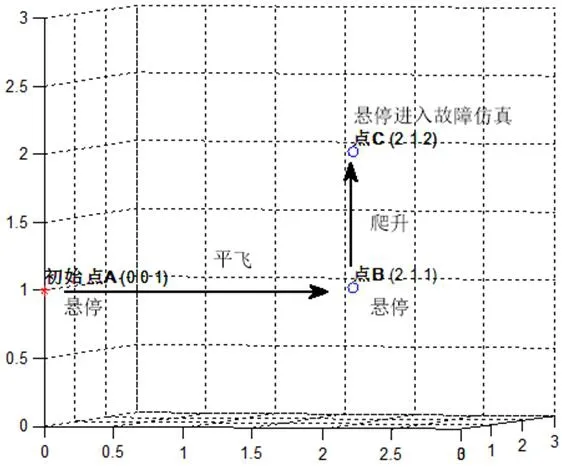
图3:仿真阶段图
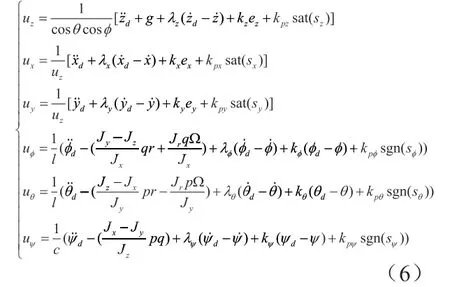
因为ψd是已知,所以有
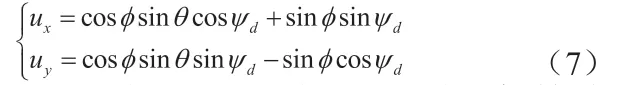
4 仿真分析与实验
在四旋翼无人机故障发生前、后两种情况下,在MATLAB/Simulink中将故障模型公式(3)作为四旋翼无人机的仿真模型,结合2中设计的容错飞行控制器完成对轨迹跟踪的数字仿真实验。
根据搭建的四旋翼无人机平台得到建模仿真参数如表1所示。容错控制器设计参数如表2所示。
为了使仿真更接近实际飞行时机体振动带来干扰的情况,在仿真中加入了高斯白噪声。仿真时假设四旋翼无人机从初始点A平飞到点B后悬停,在15s爬升到点C后悬停,这为无故障飞行仿真阶段;在23s时,通过使第四只桨叶半径减小(即为桨叶部分失效故障),造成控制效率损失,进入故障发生后的仿真阶段,仿真阶段如图3所示。根据仿真时间t=23s时,加入故障的严重程度完成数字仿真。无人机因第四个桨叶受损造成效率损失25%时的仿真结果如图4所示,仿真结果表明在0s~23s期间,为无故障发生情况,本文设计的容错控制器使得无人机能够快速、稳定地跟随期望的位置和姿态,在23s时,第四只桨叶发生故障,效率损失25%,容错飞行控制系统通过牺牲y向的位置跟随精度和滚转角的角度跟随精度,使得无人机能维持在0rad的安全姿态,仍能够保证四旋翼无人机处于稳定、安全的飞行。
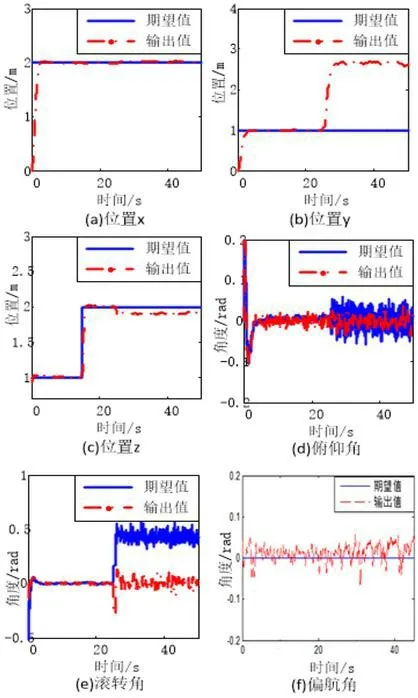
图4:桨叶半径损失25%时的飞行仿真图
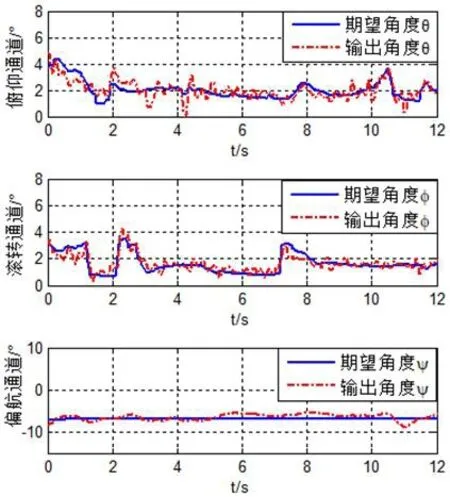
图5:四旋翼无人机飞行实验数据图
在仿真的基础在,利用自己设计的STM32飞控系统,搭建四旋翼无人机飞行平台,完成飞行试验,以进一步证明该容错控制算法的有效性。飞行试验通过地面站接收飞行时无人机的俯仰、滚转、偏航角数据,而期望值通过要控制给定,同时也将期望的俯仰、滚转、偏航角数据发送给地面站,以便后期数据的处理,其中飞行数据如图5所示。可以看出,在俯仰、滚转通道,无人机是能很好的跟随期望值,飞行是安全的,说明该飞行控制算法是成功的,且具有较强的稳定性能。
5 结论
本文针对四旋翼无人机执行器故障问题,建立其非线性数学模型,应用积分滑模理论进行了容错飞行控制律设计,完成执行效率损失0%和25%时的轨迹跟踪的数字仿真实验,实验表明该控制器具有较强的稳定性和容错能力,即使在执行效率损失25%时也能通过牺牲位置跟随的精度,保证无人机的安全、稳定飞行。在实际的飞行试验中,只完成了正常的飞行验证,飞行试验表明该控制算法具有很强的稳定性能。
