结合Curvelet变换和模糊聚类的图像融合算法

文/李伟 陈红斌

图像融合是指将通过不同传感器获得的图像使用一定的算法将其特征信息集成到同一图像中，以满足某些特定的要求。图像融合技术能够增强图像的信息利用率，提高信号探测的可靠性，在军事侦察、目标识别等领域获得了广泛的应用。小波变换具有多分辨率分析的特点，目前被广泛应用于图像处理中。但小波变换也有局限性，其变换基是各向同性的，其对图像的边缘、细节、纹理等信息表达能力有限，不能对其进行稀疏表达，在图像融合中通常会产生块状效应，降低了融合结果的质量。为了弥补小波变换的缺陷，Donoho 等人提出了曲波(curvelet) 变换理论。curvelet变换除了具有小波变换的多分辨率特性，还具有方向性。curvelet变换可在不同方向上实现多分辨率的分解，因此可以更加方便地提取图像的细节信息, 提高融合质量。

模糊技术作为一种非线性科学基础方法, 因其更符合自然界事物不确定性和随机性的规律而获得了广泛的应用。模糊聚类理论是利用元素对应某集合的隶属度来判断其归属于该集合的程度大小，以便达到区别分类的效果。FCM算法是目前比较流行的一种模糊聚类算法,该算法是针对未有明确分类的某一数据模型，利用特定的数学函数分析各种模型分量之间的距离并利用距离大小对其进行分类。鉴于事物的不确定性，各种模型分量之间往往存在交叉，各个聚类之间通常没有明确的分界，完全按照样本隶属距离的大小进行类别划分。

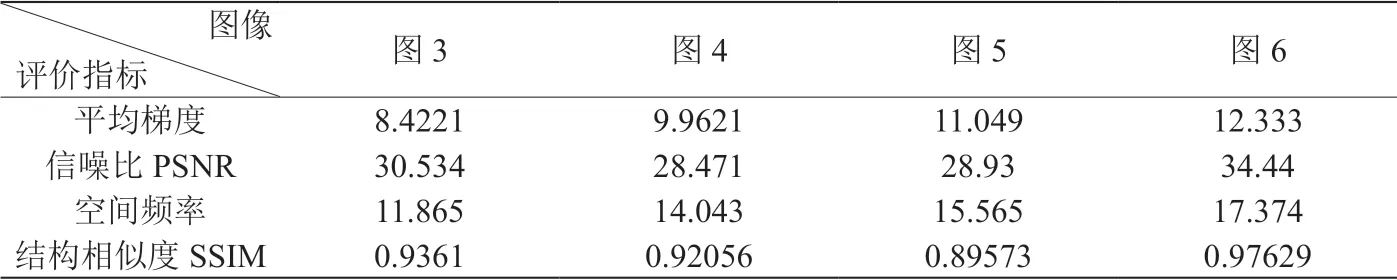
表1：不同融合方法的评价结果

本文首先利用curvelet变换将待融合图像分解成高低频分量，随后依据低频和高频分量的不同特征采取了相应的融合规则，同时将模糊聚类理论引入融合规则中，以实现对不同的图像信息进行识别分类。实验结果表明本文的算法是有效和可行的。

1 Curvelet变换

连续curvelet变换采用基函数与信号的内积形式表示：

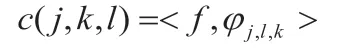
离散curvelet变换定义为：

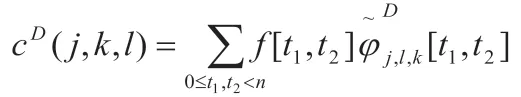
Curvelet变换可通过对采样信号进行快速Fourier 变换实现，这种实现方式被称为usfft 算法。此外还可以通过基于特殊选择的Fourier 采样的卷积即Wrapping 算法。本文采用第一种变换方法，步骤如下：

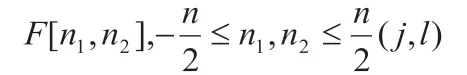
2 FCM算法

优秀的聚类方法能够有效的区分数据类别，计算出的不同类的样本差异极大。FCM算法是聚类分析的一种，它利用模糊集理论来描述样本归属于某一类别的程度大小，能够真实反映客观世界，在许多领域获得了成功的应用。

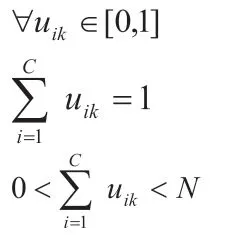
FCM算法以类内误差平方和的形式来描述，即计算每个样本到聚类中心间的距离，并乘以用隶属度的m次方进行加权。数学表达式如下：

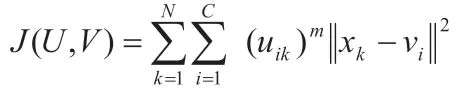
3 图像融合规则

本文融合方法的步骤为：

（1）对多聚焦图像A和B分别进行curvelet变换，表达式如下：

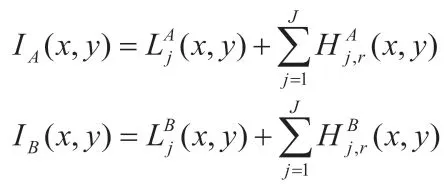
分解后得到高频分量H和低频分量L。式中，J 代表curvelet分解层数，本文分解层数为6，j表示尺度大小，r 代表方向。

（2）高频系数融合规则。

高频系数中包含着丰富的图像细节信息，如图像的边缘、纹理等重要特征信息。经过curvelet分解后，高频分量内残留的模糊信息较少，两幅待融合图像的高频分量都是有用信息，因此本文选择基于区域能量的规则进行融合。首先以像素(x,y)为中心，选取的大小为3×3区域块，计算其区域能量然后按照区域能量计算加权系数，实现高频信号的融合，规则如下：

（3）低频系数融合规则。

低频系数包含了图像的主体信息，同时也包含了大量的模糊信号，对此本文采用基于模糊聚类的方法对其进行区分。首先对低频系数进行隶属度计算，本文采用的隶属度函数为降半岭形分布，表达式如下。

图1：左聚焦图像

图2：右聚焦图像

图3：均值融合图像

图4：最大值融合图像

图5：小波融合图像

图6：本文融合图像

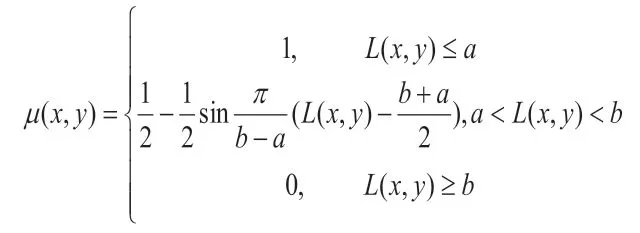
本文采用图像灰度的最大值和均值来确定截取位置的上下限，其中因此本文方法具有自适应性，可用于对不同的图像进行融合处理。最后计算相应隶属度的欧氏距离，当时，说明两幅图像信息类型相同，都是有效信息，故采用加权法融合：

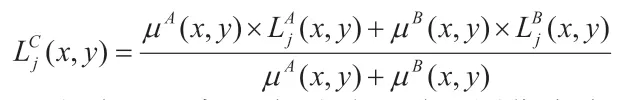
而当欧氏距离不为零时，说明图像存在噪声，则采用灰度取大的方式融合：

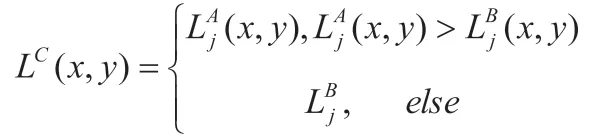
（4）对融合后得到的低频和高频系数进行curvelet逆变换，得到融合后的图像。

4 实验结果与分析

本文对多聚焦图像进行了融合仿真，图1为左聚焦图像，图2为右聚焦图像。对这两幅图像分别采用了基于本文方法、均值、最大值、小波变换方法进行融合处理，融合结果如图3-6所示。本文利用平均梯度、峰值信噪比(PSNR)、空间频率和结构相似度(SSIM)四个评价指标对融合图像进行分析，以衡量算法的融合效果。平均梯度反映了图像区域细节对比程度和纹理变化的剧烈程度，数值越大，图像层次越多；信噪比可度量融合图像中的噪声情况，数值大说明融合效果好；空间频率反映融合图像的清晰度，空间频率越大，图像越清晰；结构相似度多用来评价图像信号的结构相似性，数值大则融合图像在亮度、对比度和结构上的失真小。

通过不同融合方法获得图像的评价结果如表1所示。从表中可以看出，本文算法获得的平均梯度、峰值信噪比、空间频率和结构相似度均高于其它三种融合算法，这说明本文提出的算法在图像细节信息的保留、噪声的抑制、清晰度和对比度的提高等方面都取得了较好的结果。实验结果表明模糊聚类理论在图像融合中的应用能够有效地保留融合图像的细节信息，抑制噪声，取得良好的效果。

5 结论

本文对基于curvelet变换和模糊聚类理论的图像融合算法进行了研究。利用curvelet变换的多分辨率、多方向性和模糊聚类理论的分类特性，对高频分量采用基于区域能量加权的融合方法，低频部分采用基于模糊聚类理论的融合方法。融合结果表明，本文算法的融合效果优于对比算法，模糊聚类理论的应用能够有效地保留融合图像的细节信息，去除噪声，是一种有效的多聚焦图像融合方法。