存在爽约行为的异质患者序列预约调度优化

张文思，李金林，褚宏睿，王伟

（1.中国海洋大学 经济学院 海洋发展研究院，山东 青岛 266100；2.北京理工大学 管理与经济学院，北京 100081；3.清华大学 经济管理学院，北京 100084）

为提高医疗服务效率，缓解就诊拥堵，在新医改不断推进和移动互联等新兴技术快速发展的背景下，医疗预约服务得到高度重视和推广，与之相关的优化问题成为医疗机构和学术界关注的重点和热点[1-2]。

自Bailey[3]和Lindley[4]的开创性工作以来，医疗领域中的预约调度问题得到深入的研究[5-15]，包括患者预约数量的优化[10-11]、预约规则的设计[12-13]、患者服务顺序的确定[14-15]等。Ahmadi-Javid等[6]8指出，患者的预约调度可分为已知患者需求下的离线/同时 （offline/simultaneous）调度和考虑患者动态到达的在线/序列（online/sequential）调度，现有文献中关于离线调度的研究较多，但序列调度在现实中应用更为广泛，即需要在患者发出预约请求时便为其分配就诊时间[16]。此外，在实际医疗服务中，患者性别、年龄、初复诊情况等的不同使得患者呈现异质性（heterogeneity），患者异质性对预约系统效率最直接的影响体现在服务时间的差异[9]801[17]，因此本文将这类由于具有不同属性和特征使得服务时间不同的患者称为异质患者（heterogeneous patients）。Chen和Robinson[14]1523指出，在设计预约调度准则时应考虑患者的异质性，而患者的异质性增加了预约规则实施的复杂程度和预约系统设计成本[18]，医疗机构亟需设计一个简单可行且高效的患者预约调度机制以提高医疗服务效率和医疗资源利用率。在预约系统中可令患者的到达时间间隔为固定数值（如每隔10分钟或15分钟为一个预约时间点），这种模式可操作性较强，在预约调度理论研究[7]528[18]30-32[19]以及现代门诊实践[20]中均得到了广泛的应用。

在门诊预约调度实践中，由于患者发出预约请求的时间与实际就诊日期相隔较长，已预约患者可能由于各种原因未前来接受医疗服务，即患者爽约（no-show），患者的爽约行为会造成医院资源利用率的下降，从而会对医院的收益造成负面影响[21-23]。为此，决策者往往采用超订的方式减少患者爽约带来的影响[24]1522。Tang等[25]在患者爽约的假设下，针对包含常规患者与紧急患者的预约调度系统，提出求解最优准则的精确算法与启发式算法，Liu等[26]分析了患者爽约率与预约—就诊时间间隔的相关关系，基于排队论设计了患者超订机制，Ratcliffe等[27]建立了门诊预约容量控制和超订联合模型，分别对两种不同爽约率的患者控制预约数量以最大化期望利润。超订策略可以有效提高医疗资源利用率，但同时也会造成患者等待时间的增加和诊疗室的拥堵，因此如何确定超订患者数量也是需要重点关注的问题。

现有研究较少同时考虑患者的服务时间差异与行为特征，其中Zacharias和Pinedo[28]789在患者服务时间固定的假设下研究了爽约率和等待时间成本不同的患者预约调度模型，在此基础上，Zacharias和Pinedo[29]639，642进一步将研究扩展至多服务台系统，针对存在爽约行为的患者提出了基于超订策略的患者最优指派方案，但上述两篇文献均没有考虑到患者服务时间的异质性。Lee等[18]28-29考虑了服务时间和爽约率不同的异质患者预约调度问题，以最小化医生空闲时间成本和加班时间成本为目标，引入运作管理中均衡生产的概念，设计了初诊和复诊两类患者的预约调度方案。本文在现有研究的基础上，考虑患者爽约的行为特征，将模型扩展至多类型异质患者序列预约调度问题，以最小化患者等待时间成本、医生空闲和加班时间成本为目标，设计优化算法求解患者预约调度规则。

不同于一般的服务行业，医疗服务时间具有很大的差异性，同一科室不同类型患者的服务时间往往存在较大差异，如口腔科治疗根尖周炎、牙髓炎的时间长达60～100分钟，而治疗龋病、牙敏感平均时间仅需30分钟[30]，若采用单一预约间隔时间会导致患者等待时间延长、医疗资源利用率下降等问题。因此可考虑将患者按服务时间进行分类、分时段就诊，不同时段采用不同的预约时间间隔；文献[31]和文献[32]指出，基于患者分类的预约规则可以显著提高门诊预约调度效率，缓解就诊拥堵。将患者按照服务时间不同进行分类的分时段调度，既是预约挂号的发展趋势，也是理论研究需要关注的重点之一。基于此，本文将进一步针对不同类型患者服务时间差异较大的情况，设计基于患者分类的分时段调度规则。

一、需求已知的异质患者调度方案

考虑单服务台的门诊预约系统，首先对给定患者集合的患者最优服务方案进行优化，在固定预约时间间隔的假设下，确定患者预约时间的调度方案等价于决定患者接受服务的顺序。下面将分别在允许超订和不允许超订的假设下求解患者调度方案，以最小化患者等待时间成本、医生空闲和加班时间成本。

（一）问题描述与符号规定

本文研究单服务台的门诊预约调度问题，假设门诊每天的开放时间（即医生正常工作时间）固定为T，门诊医疗服务中不同患者的服务时间往往存在一定的差异：如初诊患者由于所需检查项目较多，一般需要更长的服务时间，如Lee等[18]32通过统计发现某诊室初诊患者平均服务时间为13分钟，复诊患者平均服务时间约为8分钟；检查项目、病情等的不同也会使得患者所需服务时间有所不同，如Huang和Verduzco[32]将某医院妇产科患者根据就诊项目分为复检、常规检查、产前检查、产后检查等8类，并指出8类患者平均服务时间存在显著差异。同时，相关文献指出，同一类别患者所需服务时间相对波动较小[18]32[29]640-641，因此可利用历史数据获得此类患者的平均服务时间；将患者服务时间固定为确定型常数的方法可以避免将服务时间假设为服从随机分布时可能会带来的对随机变量方差的过高估计[29]654-655。不失一般性，令预约患者数量为M，患者i所需服务时间为常数li，i=1，2，…，M；将医生的正常工作时间等分为N个时间槽（time slot），N≤M，每个时间槽长度即两个预约时间点的间隔固定为L，∑ili≥NL。就诊当天，已预约患者会以一定概率发生爽约，患者爽约率可根据患者特征（如年龄、性别、职业等）进行预测，并对患者进行聚类[24]1522[33]。就诊当天若患者到达系统时前序患者仍在接受治疗，会造成患者等待；若预约患者爽约，会造成医生空闲；若医生在正常工作时间内未服务完所有患者，需通过加班完成工作。决策者需要根据患者的服务时间和行为特征决定患者服务次序，若按照服务时间增序对患者进行排序，可以在一定程度上减少患者等待时间，但同样会带来服务初期医生空闲时间和正常工作时间后医生加班工作时间的延长；反之，若按照服务时间降序对患者排序，可以最大限度地减少医生空闲时间，但会增加患者等待时间，降低患者满意度。因此如何设计预约调度规则使得系统总成本最小，是本部分的核心研究问题之一。

依据上述问题设定，同时做如下假设：

假设1.所有患者均为提前预约的常规患者，不存在当天到达的紧急患者或其他未预约患者；

假设2.患者在就诊当天准时到达，不考虑患者迟到、提前到达的情况；

假设3.患者的爽约行为相互独立；

假设4.患者就诊顺序在服务开始前决定；

假设5.分配给各个患者的服务时长均为单位时间槽，即将M个患者指派至N个时间槽，且每个患者只能安排在一个时间槽就诊，每个时间槽至少安排一个患者就诊。

所用到的符号参数如下：

1.指标

i=1，2，…，M 患者指标，其中M表示等待调度的患者总数；

j=1，2，…，N 时间槽指标，N表示时间槽数量。

2.参数

li：患者的服务时间；

αi：患者的爽约率；

cw：患者的单位等待成本；

co：医生的单位加班成本；

cI：医生的单位空闲成本；

L：单位时间槽长度。

3.决策变量

a=（aij）M×N患者调度方案矩阵，若将患者 i指派至第 j个时间槽，则 aij=1，否则 aij=0。

（二）不考虑超订的患者调度方案

首先分析患者数量M=N，即不存在超订的患者排程问题。令s=（s1，s2，…，sN）表示患者在就诊当天的出现情况，若安排在第j个时间槽内的患者在就诊当天出现，则sj=1，否则sj=0。参考Lee等[18]33-34的模型设定，令bj表示在第j阶段初，服务完前j个患者额外需要的时间，则有

当j≥2时，会出现两种情况：一是bj-1≤L，表示在第j-1阶段结束时医生可以服务完前j-1个患者，此时；二是bj-1＞L，表示在第j-1阶段结束时医生没有服务完前j-1个患者，则患者j等待时间为bj-1-L。综合两种情况，可得

下面计算系统期望成本。给定患者排序方案a和患者在就诊当天的出现情况s，显然，当j=1时，患者等待时间为零。j≥2时，若sj=0，患者j不出现，因此该患者等待时间为零，若sj=1，当bj-1＞L时，第j个患者需等待前j-1个患者服务完成后方可接受服务。记第j个接受服务的患者等待时间为Wj（a，s），可得患者的等待时间为

由式（3）和式（4）可知，患者等待时间依赖于排序a和当日到达情况s。给定a和s，所有患者的等待时间总和为。

引入虚拟患者N+1，该患者的爽约率和服务时间均为零，在医生正常服务时间后增加一个长度为零的虚拟时间槽N+1，并将患者N+1指派至时间槽N+1。该虚拟患者的等待时间即为医生加班时间

医生空闲时间D（a，s）可根据医生实际工作时间和加班时间得到

由式（3）和式（6）可得系统的总成本

患者门诊预约优化问题可由下述混合整数规划（记为P）给出

由于患者行为相互独立，患者i在就诊当天的行为服从参数为αi的两点分布，给定患者排序后，患者是否爽约共有2N种可能。就诊当天第j个时间槽的患者出现的概率，随机变量 sj依赖于患者排序，每个阶段j患者的等待时间均与决策变量a和患者爽约率α相关，因此直接求解该问题比较复杂，下面对模型性质进行分析，给出最优调度方案。

给定的患者排序方案a，有

其中，E[D（a，s）]、E[O（a，s）]分别表示医生期望空闲时间和加班时间。 根据式（13）可知，最小化医生期望加班时间与最小化医生期望空闲时间等价。此外，根据 Lee等[18]36、Zacharias和 Pinedo[28]790，794、Cayirli等[34]，医生空闲和加班时间成本远高于患者的等待时间成本。基于此，本文将考虑决策者在制定决策时更偏好于降低医生加班时间成本的预约策略，提出以最小化医生加班时间成本为目标函数的松弛问题 （Relaxed Problem，RP）。

进一步地，参考Lee等[18]35的求解思路，首先在患者爽约率为零时，求解不存在医生空闲时间的患者调度方案。此时 sj=1（j=1，2，…，N），N 个患者接受服务所需时间为，即医生的实际工作时间；根据式（13），若医生空闲时间为零，则医生期望加班时间也达到最小。原问题变形为

令Γ表示（RP0）的可行集，则Γ为所有医生空闲时间为零的患者调度方案。

证明：首先证明命题的充分性，采用数学归纳法。

假设当j≤n-1时，医生空闲时间dj=0，则此时。在第 n 个阶段，，由于，可得到第n个服务阶段医生空闲时间dn=。因此可推断∀1≤n≤N，若均有成立，则医生空闲时间为零。

下面采用反证方法证明原命题的必要性，即寻找当医生空闲时间为零时患者调度方案需满足的条件。

当n=1时，若使医生无空闲时间，第一个接受服务的患者服务时间需满足L1≥L。假设j=n为第一个不满足的时间槽，即，此时，即医生空闲时间不为零，与已知条件矛盾，因此若系统不存在医生空闲时间时必然有。

根据定理1，可得到不考虑患者爽约行为时求解问题（P）最优调度方案的混合整数规划（MIP）。

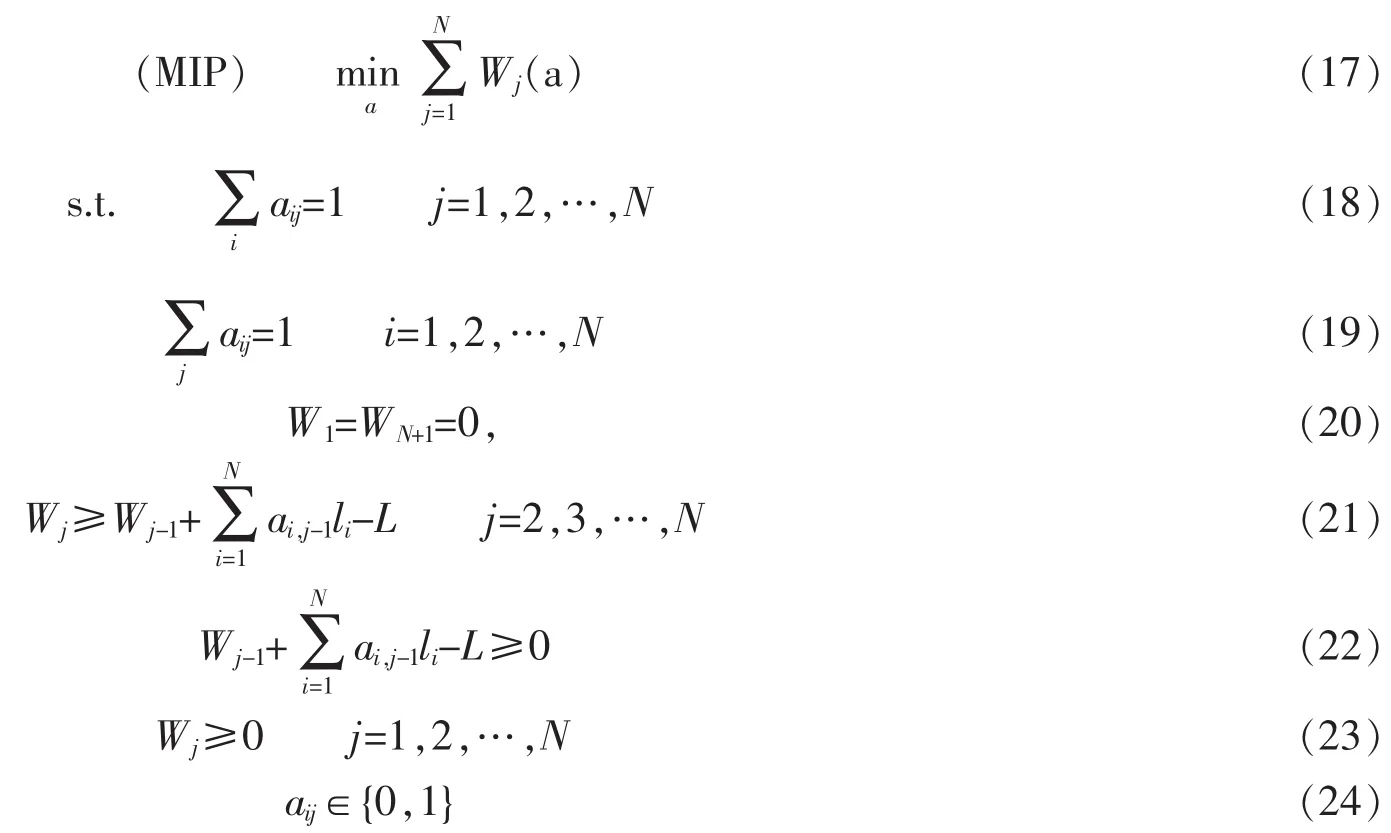
上述混合整数规划问题中，式（17）保证了每个时间槽只能有一个患者，式（17）和式（18）共同保证了所有患者都得到了安排且每个患者只能安排一个服务时间，式（20）中引入虚拟患者并利用该虚拟患者的等待时间表示医生的加班时间，式（22）限制了医生空闲时间为零，式（21）和式（23）给出了患者的等待时间约束。该问题的状态空间维度为，在多项式时间内无法通过整数规划获得最优解，根据定理1的结论，可采用动态规划或决策树的方法求解患者服务顺序的最优路径。但根据Lee等[18]38，在原模型假设下，利用动态规划求解上述问题的时间复杂度为O（NN），因此同样不适合大规模计算。基于此，将进一步分析模型性质，以设计简便算法对原问题进行求解。

推论1.假定N个患者服务时间满足lN≤lN-1≤…≤l1，令au表示患者服务顺序为服务时间降序的排队方案，即当 i=j时 aij=1，否则 aij=0，则 au给出了（RP0）问题的上界。

证明：首先证明au的可行性。由于，即单位时间槽长度L不大于所有患者服务时间的均值，因此必然存在1≤i≤N满足L≤li。记k=max{i|li≥L}，则当m≤k，显然有。而对于∀i＞k，患者 i的服务时间li小于L，当m＞k时，若要说明au的可行性，需证明。观察au不难发现，此时。 由于，因此当m＞k时必然有，即 au是问题（RP0）的可行解。

考虑到第一个患者的等待时间为零，可得所有患者的等待时间总和为

患者排序对W（a）的第二项不产生影响，因此若使等待时间最大，只需令达到最大；显然，当且仅当l1≥l2≥…≥lN时最大。

综上，au提供了问题（RP0）的上界。

根据推论1的证明过程可知，对于问题（RP0）的可行解，患者的等待时间仅取决于，由此可由如下算法求解患者调度方案。

算法1：

Step 1. 给定患者集合和相应的服务时间，令 S=0，j＝1，Patient={1，2，…，N}；

Step 2. 选择患者 i=min{k|S+li≥jL}；

Step 3. 将患者 i指派至第 j个时间槽，即 aij=1，令 S=S+li，Patient=Patient/{i}，j=j+1，若 j≤N 返回 Step 2，否则结束。

当系统中只有两种类型的患者时，Lee等[18]38证明了该算法可给出问题的最优解；当系统中存在多种类型患者，且患者服务时间互不相同时，算法1的最优性无法保证，但可作为模型的近似解为设计患者的预约调度方案提供思路。

上述分析是针对患者在就诊当天不存在爽约行为的情况展开讨论的，当患者爽约率不全为零时，则会出现医生的空闲时间。考虑到为所有医生空闲时间为零的患者调度方案，有：

证明：首先，当αi≥0时，对任意调度方案a∈Γ，医生空闲时间为零，由于，根据式（13），医生加班时间为零。给定调度方案a和向量s（s1，s2，…，sN），sj=1表示第j个接受服务的患者在就诊当天出现，sj=0表示患者发生爽约行为，则

就诊当天实际出现的患者期望数量为

此时医生期望实际工作时间为

由于不存在医生加班时间，因此医生期望空闲时间为（NL-t）。根据式（29），医生期望空闲时间与预约调度方案无关，因此对于任意t∈Γ，医生期望空闲时间相等。

假设a′∉Γ，下面比较调度方案a和a′的医生加班时间和空闲时间。首先根据集合Γ的定义，当患者不存在爽约行为时，方案a医生的工作时间T=NL，方案a′医生的工作时间T′＞NL；当存在患者爽约行为时，方案a医生的加班时间必然为零，而方案a′的医生加班时间非负，因此方案a的医生期望加班时间小于方案a′的医生期望加班时间。根据式（29）可得方案的a医生期望空闲时间为，而对于方案 a′，若第N个患者不出现，则医生可在正常服务时间NL后结束工作，否则医生服务完最后一名患者的时间在[NL，T′]之间，此时医生期望空闲时间至少为。因此方案a中医生期望空闲时间小于方案a′的期望空闲时间。

（三）允许超订的患者调度方案

根据上述分析可知，当患者爽约率不为零时会出现医生的空闲时间；实际操作中，为减小患者爽约行为对医院造成的损失，决策者往往会采用超订的策略，即接受预约的患者数量M≥N，并将超订患者指派至合适的时间槽。首先对允许超订的模型性质进行分析：

定理3.假设所有患者服务时间相等，患者和患者安排至两个相邻且无超订的时间槽，则当且仅当αj≤αk时患者j在患者k之前就诊。

证明：由于不同类型患者服务时间相等，则N个常规患者（非超订患者）被指派至N个时间槽，且每个患者恰好占用一个时间槽的服务时间。患者j和患者k安排至两个相邻且无超订的时间槽n和n+1，并假设在指派至时间槽n的患者到达前，系统中仍未接受服务的患者数量为b。当b=0时，交换患者j和患者k的顺序不会对系统成本产生影响；当b≥1时，交换两者顺序对医生加班时间和空闲时间均不会产生影响，此时患者j在患者k之前接受服务等价于

因此当且仅当αj≤αk时患者j在患者k之前就诊。

对于非超订患者，若假设时间槽长度非固定值L，而是与患者服务时间li相等，则根据定理3并结合Zacharias和Pinedo[28]792，可得到如下结论：

推论2.若非超订患者所在时间槽长度等于患者所需服务时间，且患者j和患者k安排至两个相邻且无超订的时间槽，则患者j在患者k之前就诊的充要条件为

其中，b表示患者j和k中先接受服务的患者等待时间。

结合推论2，在单位时间槽长度即患者预约时间间隔固定为L的假设下，有：

定理4.给定常规患者（即非超订患者）的排序后，将所有超订患者均安排至第一个时间槽的超订方案可以最小化医生期望加班时间和空闲时间。

证明：不失一般性，令方案a1表示将所有超订患者均安排至第一个时间槽的方案，首先注意到

其中，E[D（a1）]、E[O（a1]分别表示医生期望空闲时间和加班时间。根据式（32）可知，最小化医生期望加班时间与最小化医生期望空闲时间等价，因此只需证明方案a1的调度准则可最小化医生加班时间。

当患者类型相同时，根据Zacharias和Pinedo[28]792，定理4的结论成立。

当患者类型不同时，令方案a2表示将其中一个超订患者被安排在时间槽k（≥2），其他患者安排与a1相同的超订方案。记分别表示两种方案下第k个时间槽患者接受服务前的等待时间，显然。假设第k个时间槽内安排的患者服务时间为Lk，改变位置的患者服务时间为L′。若改变位置的超订患者在就诊当天不出现，则两种方案医生期望加班时间相等；若该患者在就诊当天出现，当时，，其中 sk∈{0，1}；当时，显然有′，此时仍有。 给定s，可得到对所有的j≥k+1，有。因此方案a1的医生期望加班时间小于a2，其他情况下的结论同理可证。

由此，超订方案a1可最小化医生期望加班时间和医生期望空闲时间。

（四）超订水平的确定

超订思想的引入可以减少患者爽约带来的医生空闲时间，提高医疗资源利用效率；然而当超订患者数量过多时，又会造成医疗诊室的拥堵，降低患者满意度。根据患者等待时间的累积效应，显然有：

定理5.在定理4提出的超订方案下，医生期望加班时间和患者期望等待时间随超订患者数量y的增加单调不减，医生期望空闲时间随y的增加单调非增。

因此如何权衡两方面的利弊，确定最优的超订水平，也是决策者重点关注的问题之一。这里给出两种可行的超订水平确定方法。

1.Poisson回归。Zacharias和Pindeo[28]795根据不同等待时间成本值记录了不同超订水平的频率，基于此利用Poisson回归模型给出了患者超订水平与患者数量、爽约率和等待时间成本的相关关系

2.期望值法。考虑到患者的爽约会带来医生空闲时间，决策者通过确定合适的超订患者数量，使得就诊当天实际出现的患者期望值等于医生的正常服务能力。当医生正常服务能力为N，患者爽约率为α时，在期望测度下，超订数量 y应满足（N+y）（1-α）=N，得到患者超订水平为

二、患者动态到达的序列预约调度启发式算法

上述研究针对给定患者集合的门诊预约系统，在已知所有患者需求的假设下建立模型求解了患者最优调度方案，通过优化患者接受服务的顺序实现降低系统时间成本的目的。但在实际中，往往需要决策者在患者发出预约请求时便告知其具体的就诊时间，因此下面将在患者动态到达的假设下，根据静态调度事先确定的调度方案，在患者发出预约请求时立即决定是否接受该患者，同时将接受预约请求的患者指派至相应的时间槽，实现患者的序列调度。

（一）单一预约时间间隔下的患者序列预约调度算法

由于患者的服务时间往往与其初复诊情况、年龄、病情、检查项目等相关，本文首先根据患者的初复诊情况、年龄等进行分类，对于复诊患者，进一步按照其病情、检查项目等的不同进行细分，并假设患者服务时间仅取决于患者类别。令I表示患者类别总数，N表示预约时间槽数量，不允许超订情况下各类患者的预约数量ni满足

根据前述患者预约调度模型，可得到不考虑超订时基于患者分类的预约调度模型

根据算法1，在不考虑患者超订的假设下，提出如下序列预约调度方案。

算法2：

Step 1.根据历史数据计算各类患者预约比例，确定各类患者的预约限制ni；

Step 2.利用算法1，得到给定各类患者数量的患者排序方案，令mi=0，t=0；

Step 3.当到达患者类型为i时，若mi＜ni，则接受该患者的预约请求将该患者分配至当前系统状态中第一个aij=1且未指派患者的时间槽，mi=mi+1，t=t+1，否则拒绝；

Step 4.当t=N时，结束。

当患者存在爽约行为时且允许超订时，根据定理4，在系统中存在多种类型的患者时，有如下结论：

推论3.给定常规患者（即非超订患者）的排序后，将所有第i类超订患者均安排至第一个第i类患者所在时间槽的超订方案可以最小化医生期望加班时间和空闲时间。

证明：简便起见，令方案A表示将所有第i类超订患者均安排至第一个第i类患者所在时间槽的超订方案，首先注意到

当患者类型相同时，方案等价于将所有超订患者均安排至第一个时间槽，根据Zacharias和Pinedo[28]790-791，显然结论成立。

当患者类型不同时，假设就诊当天有xi个第i类患者出现，令方案A′表示其中一个超订患者被安排在第二个i类型患者所在时间槽，其他患者安排与相同的超订方案。假设第一个i类型患者所在时间槽记为k1，第二个i类型患者所在时间槽记为k2，记分别表示两种方案下第k个时间槽的患者接受服务前2的等待时间。若改变位置的i类型患者在就诊当天不出现，则两种方案的医生期望加班时间相等；若该患者在就诊当天出现，当时，，其中 sk2∈{0，1}；当时，显然有，此时仍有，因此方案的医生期望加班时间小于A′，其他情况下的结论同理可证。

由此，超订方案可最小化医生期望加班时间和医生期望空闲时间。

根据推论3，将超订患者全部放在第一个时间槽的调度方案（front loaded）[35]可以最小化医生期望加班成本和空闲成本。尽管这种处理超订患者的方式会增加患者等待时间，但根据Lee等[18]36，由于医生空闲和加班会造成医疗检查设备空转或超时工作，该成本往往远大于患者等待时间成本，因此在实际操作中将超订患者安排至第一个时间槽的方式不失为一种可行的方案。

（二）考虑患者分类的分时段预约调度算法

患者由于病情、检查项目的不同，会出现不同类型患者服务时间差异较大的情况，此时若令单位时间槽长度均统一为L，将服务时间差异较大的患者进行统一调度，将会导致患者等待时间或医生空闲时间产生较大的波动，降低服务效率。基于此，可将患者根据服务时间的不同分成多个时段（block），每个时段可包含多类患者，且患者服务时间差异较小，将不同时段中的患者按照算法2的方法进行分别调度，实现弹性预约时间间隔下的患者分时段就诊，以提高医疗资源利用率。以医疗设备检查为例，来自同一科室的患者所需检查时间由于病情类型的不同会存在一定的差异，但同一科室的患者检查时间差异往往小于不同科室患者之间的检查时间差异；因此可将患者按照送检科室的不同确定相应的服务时间间隔，分别设计最优调度方案。

假设系统服务时间分成个K时段，每个时段中有Ik类患者，各时段预约时间间隔可根据患者服务时间确定。根据历史数据，计算不考虑超订情况下各类患者预约比例，使得第k个时段中时间槽数量Nk满足

其中，ni为各类患者的预约数量；k∈N+。

对每个预约时段中的患者，考虑患者的动态到达过程，设计患者序列预约调度方案如下。

算法3：

Step 1.根据算法2，得到不考虑患者超订的排序方案，并利用式（33）或式（34）给出各类患者的最优超订水平yi；

Step 2. 赋初值，令 mi=0，t=0；

Step 3.当到达患者类型为i时，若mi＜ni，则将该患者分配至当前系统状态中第一个aij=1且未指派患者的时间槽，mi=mi+1，t=t+1；

Step 4.若ni≤mi＜ni+yi，将该患者分配至第一个aij=1的时间槽，否则拒绝；

Step 5.当t=N+∑iyi时，结束。

利用算法2和算法3，可设计如下算法得到整个系统的序列预约调度方案。

算法4：

Step 1.根据历史数据获得患者到达率和平均服务时间，将预约窗口分成K个时段；

Step 2.对每个预约时段，根据算法2得到不考虑患者超订的预约调度方案；

Step 3.当患者到达时，根据患者类型选择分配的时段，利用算法3，根据当前系统状态接受或拒绝患者请求，并将接受预约请求的患者指派至相应的时间槽。

三、数值算例

首先对算法的有效性加以说明，考虑患者爽约率为零的情形，目标函数为在已知患者类型和数量的前提下，求解满足医生空闲时间为零且患者等待时间和医生加班时间最小的调度方案。假设系统中共有4种类型的患者，分别记为A、B、C、D，患者服务时间各不相同，为保证计算结果的有效 性 ，令 lA∈[8，12]，lB∈[11，13]，lC∈[10，15]，lD∈[5，10]，各类患者数量 ni∈[0，5]。 表 1对比了患者服务时间，分别取 lA=9，lB=12，lC=13，lD=8，预约时间间隔L=10，系统中存在不同类别和不同数量的患者时，启发式算法1获得的预约策略和由枚举法获得的患者最优排序。通过结果可以发现，启发式算法获得的患者排序虽与通过枚举法最优排序存在一定的差异，但患者等待时间差距并不大；而且当患者类型和患者数量较多时，启发式算法所需要的计算时间明显低于通过穷举获得最优解所需要的时间。

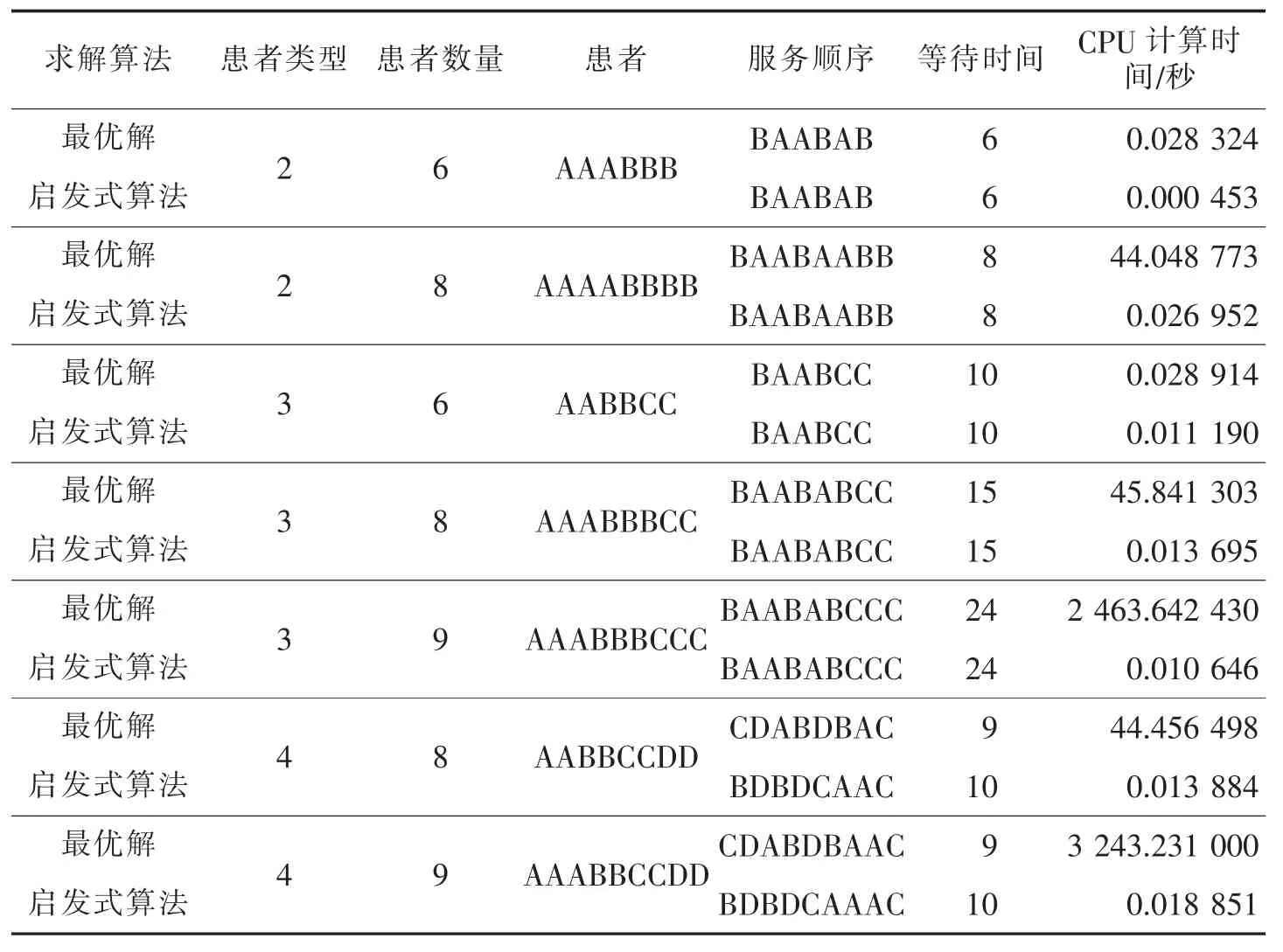
表1 最优解与启发式算法结果

下面分析不同预约调度模式下的系统时间成本。假设服务时间可分为20个时间槽，预约周期T=30，在预约周期内共有4种类型患者发出预约请求，当患者到达时决策者需根据患者类型和当前预约状态决定是否接受该患者预约请求，并将接受预约的患者指派至合适的时间槽，使得系统总时间成本（包括患者等待时间、医生空闲时间和加班时间）最小。4类患者的服务时间向量为l=（7，14，17，26），根据历史数据，4类患者需求比重为 p=（0.2，0.3，0.2，0.3），患者爽约率为 α＝（0.2，0.3，0.4，0.2）。 为便于分析，将目标函数利用空闲成本单位化，即令cI=1，患者单位等待成本和医生加班成本可参考Robinson和Chen[21]338，令co=1.5，cw=0.5。考虑如下4种预约方案：

1.服务时间等长的预约调度（Non-block Scheduling）。首先考虑服务时间间隔相等的预约调度模式，并令单位时间槽长度L=15，利用算法2决定患者排序。

2.弹性服务间隔的分时段调度（Block Scheduling）。根据患者服务时间的差异，对患者进行分时段调度；在上述问题假设下，可将服务时间分为两个时间段（block），每个时间段包含10个时间槽，其中第一个时间段只安排前两类患者预约，且单位时间槽长度L1=10，第二个时间段只安排后两类患者预约，单位时间槽长度L2=20，利用算法4获得的预约方案决定患者服务顺序。

3.随机预约调度模式（Random Scheduling）。令单位时间槽长度L=15，预约周期内，接受患者预约请求直至预约人数达到预约上限；对于非超订患者，随机安排患者排序。

4.Open Access（OA）。即不允许预约患者，所有患者均在就诊当天发出服务请求，不存在患者的爽约行为。为和前述预约模式保持一致，本文提出的Open Access策略假设各个时间槽长度相等且固定，若患者总数量小于医生正常服务能力，决策者接受当前患者预约，并将患者按到达次序分配至各时间槽。

对于前3种预约方案，采用超订策略应对患者的爽约行为。首先根据患者需求比例决定4种类型常规患者（即非超订患者）的数量，进一步利用式（34）获得各类患者超订水平，结合推论3，将所有超订患者均安排至该类患者所在的第一个时间槽。对患者到达过程和行为特征进行仿真，可得到4种预约调度模式下的系统平均成本如表2所示。根据表2可发现，算法2和算法4获得的预约调度方案明显优于随机预约调度模式和OA模式，而将患者按服务时间进行分时段调度可在一定程度上降低系统成本，提高医疗资源使用率。

表2 不同预约方案下的期望成本

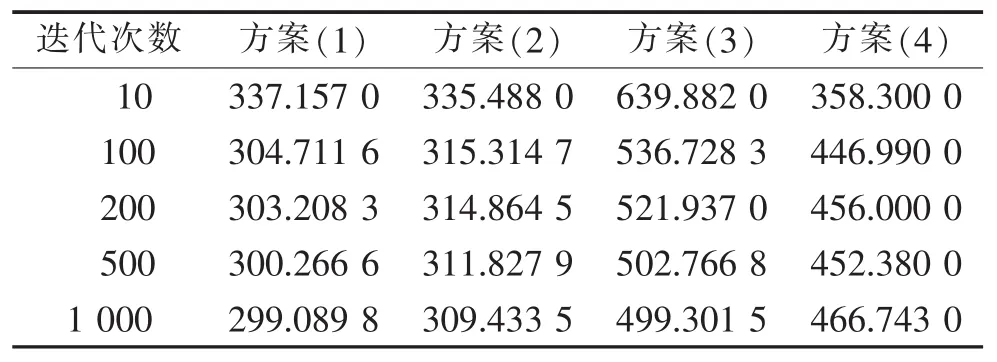
表3 不同预约方案下的患者等待时间

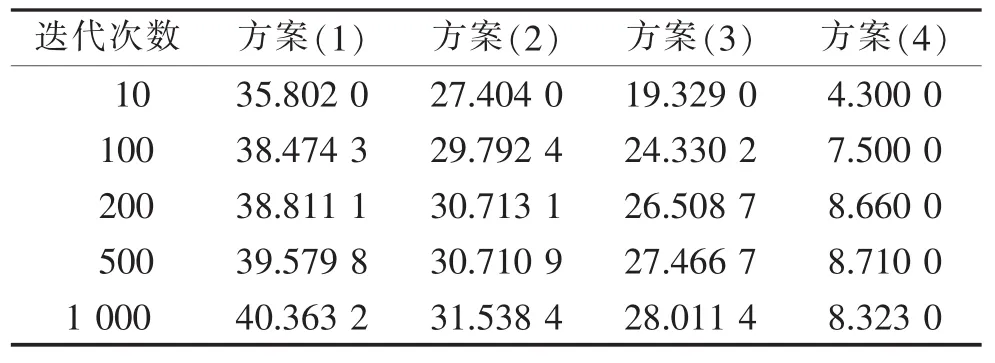
表4 不同预约方案下的医生空闲时间

表5 不同预约方案下的医生加班时间

表3～表5分别比较了不同预约方案下患者的等待时间、医生空闲时间和加班时间，可以发现，与随机预约调度模型相比，根据算法2和算法4设计的两种预约调度方案可以很大程度地减少患者等待时间；与OA模式相比，算法2和算法4明显减少了患者等待时间和医生加班时间。此外，允许弹性服务时间间隔的分时段调度方案与服务时间间隔等长的方案相比，医生的空闲时间和加班时间较低，而在实际情况中，医生空闲成本和加班成本往往远高于患者的等待时间成本，因此将患者进行分时段调度有一定的现实意义。

图1～图3进一步对比了不同预约周期对医生期望空闲和加班时间以及患者期望等待时间的影响。不难发现，随着预约周期的增加，医生空闲时间呈现逐渐减少的趋势，而医生加班时间和患者等待时间则逐渐增加。其主要原因在于，对于方案（1）和方案（2），由于各时间槽分配的患者类型已提前确定，当预约周期较短时，可能会由于发出预约请求的患者数量较少，导致部分时间槽空缺，从而造成医生空闲时间较长，同样的，对于方案（3），预约周期较短时，患者数量较少，患者爽约行为更容易带来医生的空闲时间；而随着预约周期的增加，患者预约数量可达到预约上限，由此会增加患者的等待时间和医生加班时间。此外，从图1～图3中还可发现，随着预约周期的增加，系统所接受的预约患者数量逐渐接近预约上限，因此医生空闲时间和加班时间、患者等待时间变化量逐渐减小，系统状态趋于稳定。

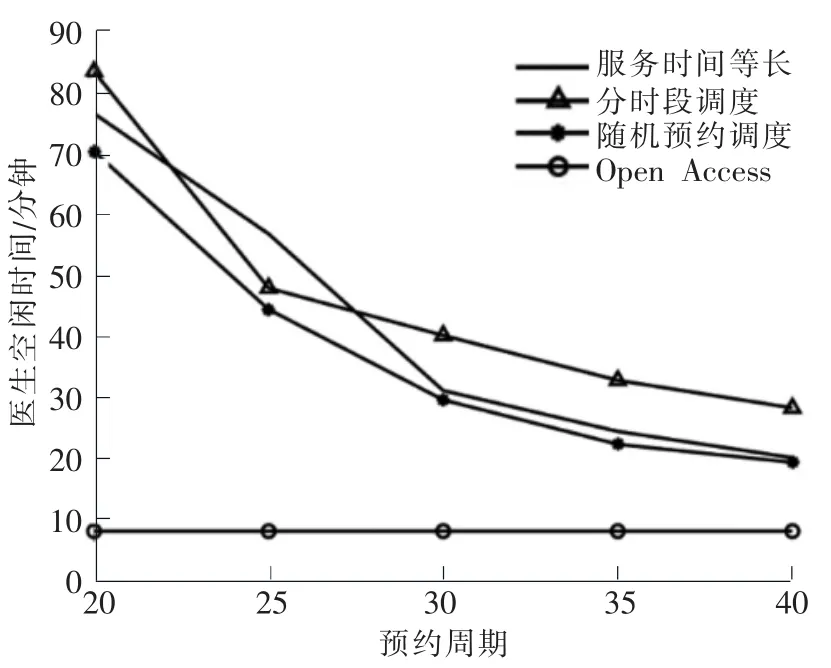
图1 不同预约周期下的医生期望空闲时间

图2 不同预约周期下的医生期望加班时间

图3 不同预约周期下的患者期望等待时间

四、结论与展望

本文以服务时间不同的异质患者为研究对象，结合患者爽约行为，以最小化患者等待时间成本、医生加班和空闲时间成本为目标，研究了固定预约时间间隔下的异质患者序列预约调度问题。首先在给定患者集合的情况下，建立混合整数规划模型，分别在不允许超订和通过患者超订减少患者爽约影响的假设下设计患者预约调度规则；在此基础上，设计动态预约调度方案，当患者发出预约请求为患者安排就诊时间。最后，当不同类型患者所需服务时间差别较大时，设计基于患者分类的分时段预约调度方案，以减少医生空闲时间和加班时间，从而降低系统运营成本。

根据本文研究结果，在医疗服务实践中，可针对服务时间差异较大的患者设计不同预约时间间隔，采取分时段的方式对患者进行调度，当患者发出预约请求时为其分配合适的就诊时间，以提高医疗服务效率和资源利用率。此外，现实中对于需要复诊的患者，医生往往选择在当前服务结束时为其安排下一次的就诊时间，为减少患者爽约，医生可根据患者调度方案结合患者对就诊时间的偏好，为其确定预约时间；若在服务开始前仍有空余时间槽未被预约，医生也可通过临时加号的方式，通知未能成功预约的患者前来就诊，减少医疗资源的闲置。本文研究结果可为服务时间不同的门诊患者预约调度问题提供一个易于操作的有效解决方案，此外，本文提出的决策方法也可应用于如金融服务、法律咨询等存在不同类型顾客的服务行业，提高排队系统的服务效率，降低服务成本。

本文假设患者爽约率为外生变量，在现实就诊过程中，患者对服务时间、医生的选择偏好往往会对患者爽约率产生影响，如何在设计预约规则时同时考虑患者的选择偏好以提高患者满意度和医疗服务效率，是后续研究可以探讨的方向之一。