一种高空台特种调节阀通用特性修正方法
2019-09-14缪柯强朱美印但志宏裴希同
缪柯强,王 曦,朱美印,张 松,但志宏,裴希同
(1.北京航空航天大学能源与动力工程学院,北京 100191;2.先进航空发动机协同创新中心,北京 100191;3.中国航发四川燃气涡轮研究院航空发动机高空模拟技术重点实验室,四川绵阳 621000)
1 引言
航空发动机高空模拟试验台(简称高空台)是评估发动机高空性能的重要物理设备,凡独立自主发展航空工业的国家,都很重视高空台的建设[1]。为获得与战术技术指标日渐提高带来的急剧变化的飞行条件相匹配的环境模拟能力,高空台对功率和流量的需求越来越大[2-4]。为此,我国从俄罗斯引进了大流量轮盘式特种调节阀,用于高空台进气管网的气路调节。但俄罗斯厂商提供的阀门流量特性与高空台试验过程中测得数据存在高达15%的误差[5],难以满足高空台伺服调控系统设计要求。加之高空台试验成本高,无法为阀门进行单独试验以获得阀门流量特性[6-7]。所以利用现有特性,对其进行修正以建立准确的流量模型,对高空台伺服调控系统设计十分重要。
目前,国内主要采用在已有特性的基础上结合试验数据手动调整特性图的方法对阀门进行修正,但该方法不仅工作量巨大,而且对工程经验有很高的要求,为此国内学者开展了大量的特性修正算法研究。裴希同等[8]提出一种基于经验公式的流量系数求解算法,但该算法对经验公式的准确性有高要求;朱美印等[5]提出一种基于数据的间接特性修正方法,但该方法数据处理过程复杂,修正分类繁多,工作量大。邹包产等[9]利用神经网络直接对流量计算结果进行修正,但对单一特性线上流量计算结果的修正不满足应用于高空台的复杂调节环境的要求。为此,本文提出一种基于神经网络和试验数据的综合特性修正方法。此方法不仅考虑了修正后的精度,而且同时兼顾了高空台不断产生新数据且数据较集中的特性对修正算法的便利性、可重复操作性和全局可靠性的要求,保证了修正特性有效提升模型精度的同时不带来工作量的大幅提升。
2 流量特性模型
流量特性模型是一种流量与各影响参数(如工质的种类、温度、压力和流通面积等)之间的函数关系。考虑到特种调节阀内部由一系列孔板结构组成,可使用孔板结构理论为特种调节阀建模。对于工质为气体的孔板结构阀门,理论流量特性模型[8]为:
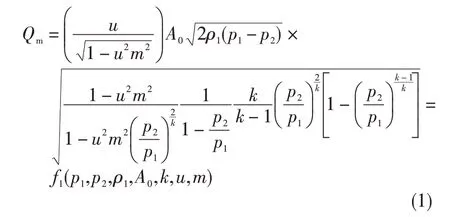
式中:Qm为通过节流孔的气体的质量流量;p1为阀前压力;p2为阀后压力;ρ1为阀前来流密度;A0为节流孔面积;k为气体绝热指数;u为流束收缩系数,等于流束收缩最小截面面积Amin与调节阀截面面积A之比;m为截面面积比,且m=A0/A。
然而在实际试验中,Amin难以获得,故式(1)所示理论模型难以在工程中用于特种阀流量计算。为此,本文使用马卡洛夫基于试验数据拟合法提出的质量流量公式(式(2))[10]建立特种调节阀流量特性模型。
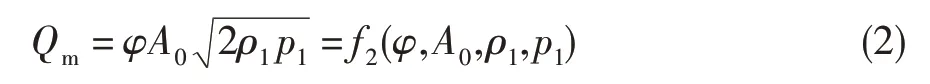
式中:φ为试验数据拟合法表示的调节阀流量系数。
虽然式(2)中的φ、A0和ρ1是试验中不可直接测得的参数,但这3 个参数可使用直接测量参数计算获得。在特种调节阀中,A0与试验直接采集数据阀门开度Vp之间有线性对应关系:

式中:a为常数。
高空台管网中ρ1的计算公式为:

式中:R为气体常数,T1为阀前温度。
马卡洛夫在大量试验数据分析的基础上,得到了定绝热指数下φ和阀门前后落压比pr(pr=p1/p2)及m之间存在式(5)所示的插值数据关系[10]。而现有高空台环境下A为定值,故m仅与Vp相关,如式(6)所示,所以φ可表述为式(7)所示的直接测量量的函数。

综上所述,特种调节阀的流量特性模型如式(8)和图1 所示。

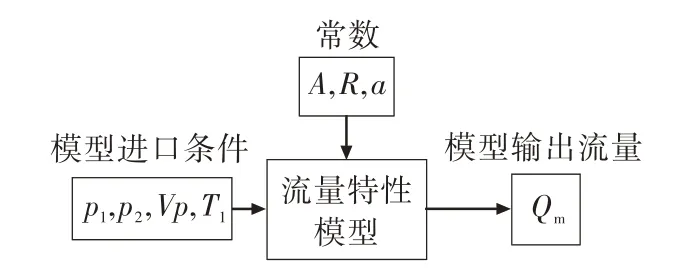
图1 流量特性模型输入输出示意图Fig.1 Input and output diagram of mass flow characteristic model
由于式(5)是在大量试验数据基础上得出的插值关系,没有理论数学表达式,故将式(5)从式(8)中分离,得到流量特性模型的数学描述,如式(9)所示。从而,图1 中的流量特性模型内部结构如图2 所示(省略常数输入)。

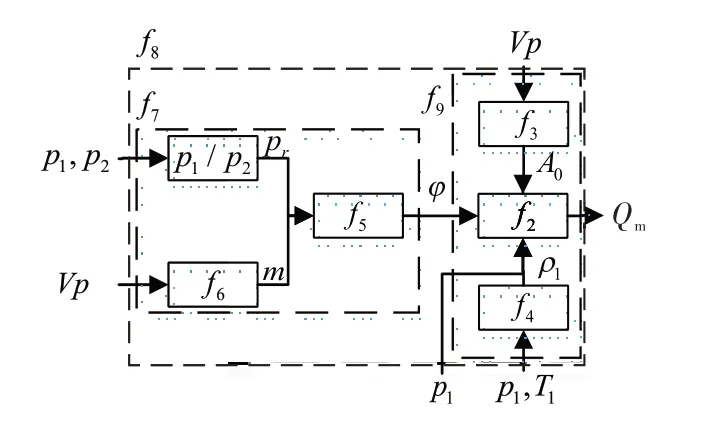
图2 流量特性模型内部结构Fig.2 Internal structure of mass flow characteristic model
3 试验数据预处理
一次高空台试验会模拟数十个高空状态之间的变化,耗时十几个小时,采集上亿个数据点。由式(8)可知,需用到的稳态点试验数据为p1、p2、Vp、T1和Qm,将由此获得的第i组数据记为xi={p1,p2,Vp,T1,Qm}。
试验数据中,同一稳态过程包含大量数据组xi,对应同一种阀门工作状态存在大量冗余。为去除冗余并消除噪声对数据精度的影响,计算同一稳态过程中所有xi的平均值,则第j组稳态过程均值为。
对xj中数据进行处理,计算稳态点平均落压比和稳态点平均截面面积比,进而(c为常数),获得第j组训练样本点。
从6 次高空台试验的所有数据点中提取290 组稳态过程数据并计算均值,得。使用X中数据计算,获得训练样本点组。将其中前4 次试验的190 组训练样本点用于训练新特性图,记为,剩余的100 组训练样本点用于验证新特性图的有效性,记为。
由于高空台试验时有具体的试验目标,所以特种阀的阀门开度会集中在某一范围内。本文中所有290 组数据点数据中的阀门开度分布如图3 所示。若仅以试验数据进行训练,则训练结果在小开度(15°以下,对应m<0.064)和大开度(60°以上,对应m>0.257)的情况下严重失真,影响模型的稳定性。计算稳态点平均流量系数为此,将表1 中的初始特性以数据点形式加入拟合数据的神经网络训练样本点进行全局补足,额外获得260 组全局训练样本点,保证了训练后的特性在数据点较少的区域也合理有效,从而确保了模型的稳定性。最终,用于训练神经网络的样本点为Ytotal={Y1,Yplus}。
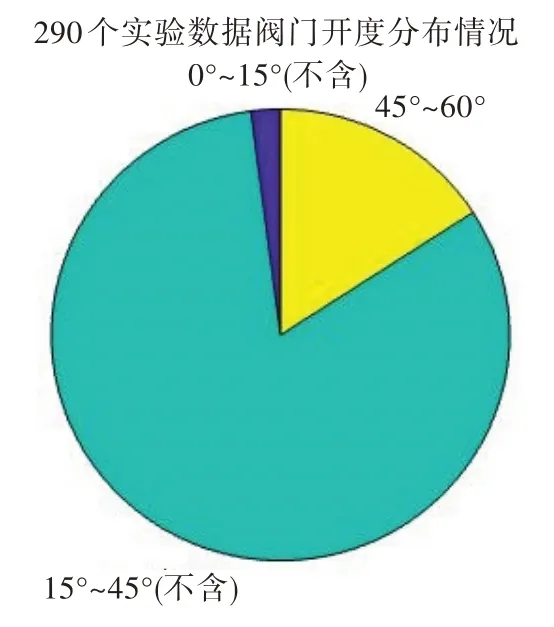
图3 290 组试验数据中阀门开度分布情况Fig.3 Valve opening distribution of the 290 sets of experimental data
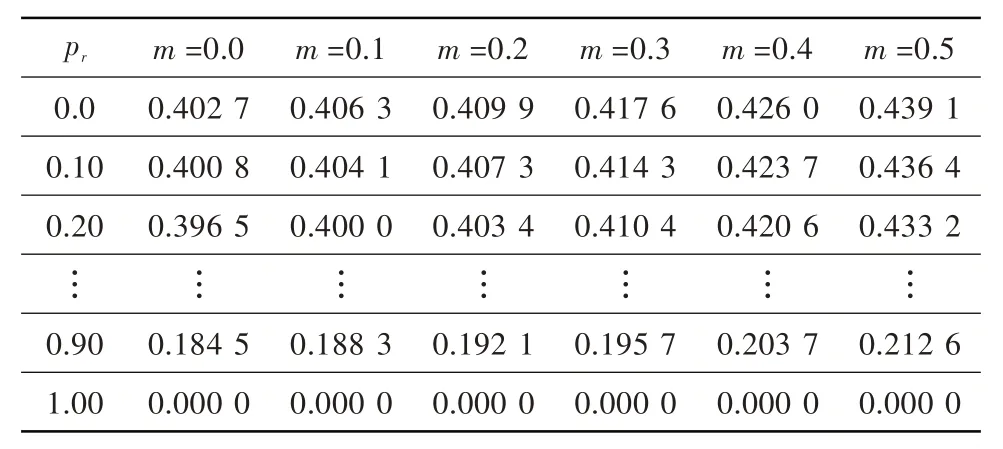
表1 初始特性表Table 1 The initial characteristic table
4 神经网络修正方法
φ=f5(pr,m)的BP 神经网络结构可用图4 表示,隐层层数和隐层节点数可调,其中ωij和ωjk为节点之间的连接权值。

图4 流量特性的BP 神经网络结构Fig.4 The structure of the mass flow characteristic BP neural network
4.1 神经网络模型设置
考虑到训练样本Ytotal的样本量为450,对训练速度要求不高,由此选择隐层层数为10,学习速率为0.01。在Matlab 界面中的神经网络模型结构如图5 所示。
4.2 算法和性能函数设置
为获得更快的收敛速度并避免陷入局部极小解,选择使用Levenberg-Marquardt(LM)算法[11]。同时,选取Mean Square Error(MSE)作为神经网络性能函数,即最小化式(10)所示的均方误差。在Matlab 中显示如图6 所示。
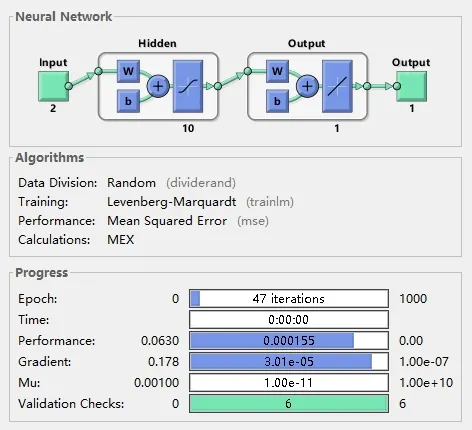
图5 Matlab 中的神经网络模型结构Fig.5 The structure of the mass flow characteristic BP neural network in Matlab
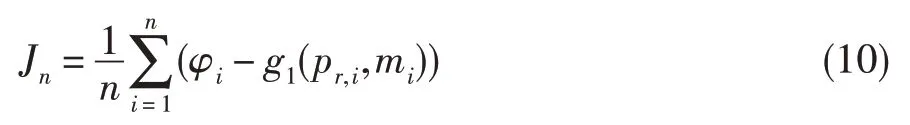
式中:Jn为均方误差,n为样本点数,下标i表示第i个样本点。

图6 神经网络算法设定Fig.6 The algorithm setting for BP neural network
4.3 神经网络训练
设置训练时数据的使用方式为80%用于训练、10%用于有效性检验、10%用于测试训练结果。训练进程如图7 所示,训练的回归分析结果如图8 所示。总体拟合可决系数R2=0.9832=0.966,表明同输入下网络输出值与试验值之间吻合程度高。将训练完成的网络记为φ=g5(pr,m)。

图7 神经网络训练进程Fig.7 The training process of BP neural network
4.4 修正特性图获取

图8 回归分析结果Fig.8 The results of regression analysis

表2 修正后的特性表Table 2 The characteristic after correction
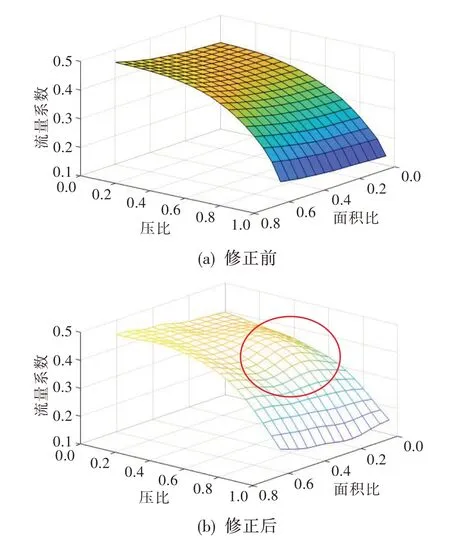
图9 修正前后的特性图Fig.9 The characteristic maps before and after correction
将表1 的横纵坐标点依次输入新网络φ=g5(pr,m),获得在原特性图基础上基于神经网络和试验数据修正得到的新特性图,结果如表2 和图9(b)所示。相比于图9(a)中修正前的特性图,修正后的特性图在试验数据集中区域(图9(b)中红圈位置)的流量系数变大,且在缺乏试验数据的区域与原特性图基本保持一致。
5 仿真对比验证
使用修正后的特性图替换原特性图得到新的流量特性模型(式(11)),利用前文保留的100 组稳态点数据点Y2进行仿真验证。

在给定试验数据中的相同进口环境(p1,T1,pr)和特种阀阀门开度条件下,分别由原特性模型式(9)和新特性模型式(11)计算出口流量并与试验数据进行对比,同时计算流量的相对误差(为直观展现相对误差大小,本文取相对误差的绝对值)。
由图10 中的数据对比可看出,原特性模型计算流量相对于试验测得流量偏小较多,而修正后的特性模型计算流量与试验测得流量误差减小。从图11 中的相对误差对比可进一步看出误差减小的程度,流量最大相对误差从16.1%减小至8.4%,减小47.8%;流量相对误差绝对值的平均值从8.3%减小至2.3%,减小72.6%。

图11 特性修正前后仿真结果相对误差的绝对值Fig.11 The absolute value of the maximum relative error before and after correction
6 结论
针对原始阀门流量特性与高空台试验过程中测得数据存在较大误差的问题,提出一种基于试验数据和原始特性图数据的全局补足高空台特种调节阀神经网络通用流量特性修正算法。对试验数据预处理,去除冗余信息和噪声干扰,提取试验数据中的稳态信息。同时,提取原始特性图中的全局信息对训练样本点进行全局补足。以阀门前后落压比、截面面积比为神经网络输入,以流量系数为神经网络输出,利用神经网络对高空台特种调节阀的特性进行修正,获取新的流量特性。新旧流量特性模型仿真对比验证表明,修正后的流量计算误差减小,流量特性模型精度得到提高。
