基于自然最近邻的离群检测方法研究

李士果 卢建云 邓剑勋

摘 要：在实际应用中，近邻技术具有简单、快速、高效的特点，受到研究人员的青睐。近来自然最近邻被提出并应用到离群检测和聚类中，鉴于自然最近邻消除了参数k设置的特点，本文将自然最近邻的概念应用到逆k最近邻、互k最近邻、共享k最近邻中，提出了自然逆最近邻、自然互最近邻和自然共享最近邻。并将提出的3种算法在离群点检测中进行了实验对比分析。实验结果表明自然逆最近邻和自然互最近邻能够有效发现局部和全局离群点。

关键词：近邻技术;离群点检测;自然最近邻;数据挖掘

文章编号：2095-2163（2019）04-0040-06 中图分类号：TP391 文献标志码：A

0 引 言

近邻技术是数据挖掘和机器学习的重要技术之一，被广泛地应用到分类、聚类、异常检测、协同过滤、图像处理等研究领域。在实际应用中，近邻技术具有简单、快速、高效的特点，一直以来受到研究人员的重视。目前存在的近邻技术有k最近邻、互k最近邻、逆k最近邻、共享最近邻、自然最近邻。这些近邻技术各有特点，自提出以来都得到了广泛的应用。近来自然最近邻被应用到离群检测和聚类中，并取得了比较好的效果。鉴于自然最近邻能够消除参数k设置，本文将自然最近邻这一特点应用到其它近邻中，提出了自然逆最近邻、自然互最近邻、自然共享最近邻的概念，并给出了相应的算法描述。在离群检测应用中，对提出的自然逆最近邻、自然互最近邻、自然共享最近邻算法进行了实验对比分析，实验结果表明自然逆最近邻和自然互最近邻能够有效发现局部和全局离群点。

本文的主要贡献如下：

（1）结合自然最近邻消除参数k设置的特点，提出了无参的自然逆最近邻、自然互最近邻、自然共享最近邻的概念，并给出了相应的算法描述;

（2）在离群检测应用中，对提出的算法进行了实验对比分析，实验结果表明自然逆最近邻和自然互最近邻能够有效地检测局部和全局离群点。

1 相关研究

最近邻概念直观、简单，认为一个对象与离其最近的对象具有相同的特点，最初被应用于基于示例的学习方法中。从概率的角度出发，可以通过多个对象投票的方式来确定被分类模式的标签，则引入了k最近邻的概念。k最近邻有非常广泛的用途，例如模式分类、机器学习、数据挖掘等领域[1]。在模式分类中，k最近邻作为分类器对待识别模式进行分类，考虑每个近邻的贡献不同，出现了基于权重的kNN[2]分类方法。在图像分割中，kNN与贝叶斯网络结合，出现了贝叶斯kNN图像分割算法[3]，还有kNN作为启发的区域迭代的图像分割算法[4]。在数据挖掘中，k最近邻与距离结合衡量数据集中对象的密度，被用来进行离群点检测。对于聚类应用，k个最近邻能够形成子图，通过相似度度量函数，不断合并相似的子图，直到满足需要得到的子图数目，从而实现聚类。互k最近邻比k最近邻要严格，加入了一个限制条件，即要求2个对象p和q出现在对方的k最近邻域，则p和q为互k最近邻。通常，构建的互k最近邻图更加紧密，常被应用到去噪、分类中[5]。共享k最近邻进一步考虑了对象p和q邻域共有的近邻数目，采用量化的方法来度量两个对象的相似程度，常被应用到离群检测、聚类中[6]。逆k最近邻与k最近邻具有相反的概念，是考虑一个对象对其周围对象的影响，被应用于决策支持、资源定位与营销等研究领域[7]。目前，对逆k最近邻的研究主要集中在如何高效地进行搜索[8]。

最近提出的自然最近邻概念具有自适应的特点，不需要显示地指定参数k的值，而是通过迭代计算得到给定数据集的自适应k值。自然最近邻被应用到高维数据结构学习、离群检测、分类、聚类等场景[9]。自然最近邻在形成的过程中，带有密度信息和离群信息，能够被应用到局部密度估计和离群检测[10]。

2 近邻技术

本节中，给出了互k最近邻、逆k最近邻、共享k最近邻和自然最近邻的定义，并对各种近邻的特点进行了分析。

2.1 互k最近邻

在k最近邻的基础上，增加一个限制条件，即2个对象要互为k最近邻，这就是互k最近邻的思想。2个对象互为k最近邻，恰恰反应了2个对象之间的紧密程度。相对于k最近邻反映的是单边关系，而互k最近邻描述的是一种双边关系。

2.2 逆k最近邻

求解k最近邻时，一个对象总是返回k个最近邻，每个对象拥有最近邻的数目是不变的。在实际应用中，对于密度度量，处于稀疏空间的对象并不总是有k个最近邻。逆k最近邻是与k最近邻具有相反含义的一种最近邻概念。k最近邻反应的是查询对象离某个被查询对象最近，而逆k最近邻描述的是被查询对象对数据集中其它查询对象的影响，被查询对象能够影响的对象数目可能有一个、多个或者是没有。

2.3 共享k最近邻

互k最近邻描述了2个对象之间的相近或紧密程度。这种度量关系比较简单，只有紧密、不紧密，或者相近、不相近这样的二元关系。共享k最近邻突破了这种二元关系，采用一种可以量化的度量方法，即衡量2个对象共有最近邻的数目，这种量化度量方式很好地表达了相对程度。

2.4 自然最近邻

在k近邻技术中，参数k是需要设置的，对于不同的应用场景，参数k的设置也不尽相同，往往通过经验分析得到合适的参数值。为了减轻参数k对最近邻计算结果的影响，邹咸林等人提出了自然最近邻概念[9]。求解自然最近邻时，不需要指定参数k或者邻域半径ε，其是一种无尺度的最近邻概念。求解自然最近邻的核心思想是设置计算的终止条件，整个计算过程是对给定数据集的一个自适应过程，当迭代计算收敛时，得到数据集中每个对象的自然最近邻。自然最近邻数目是一种量化的度量方法，能夠反映数据集疏密分布情况。求解自然最近邻的方式可以有多种，表现为迭代计算的终止条件不同。

3 自然最近邻在其它近邻中的应用

本节中，给出了自然逆最近邻、自然互最近邻和自然共享最近邻的定义和算法描述。自然最近邻概念的要点是“数据集中最离群的数据对象都至少有一条路径到达”，这个特点使得每个对象具有不固定尺度的近邻数目，也减轻了参数k对最终近邻数目的影响。

3.1 自然最近邻定义

在定义7中，自然共享最近邻不是指2个对象p和q共有的近邻对象，而是指p和q的一种关系，如果p和q共有的近邻数目大于等于m，则p和q是一种自然共享最近邻的关系。下面给出定义5到定义7的算法实现描述。

3.2 自然最近邻算法描述

算法1 自然逆最近邻算法（NRNN）

输入：数据集D包含n个对象

输出：D中每个对象的自然逆最近邻数目

算法描述如下：

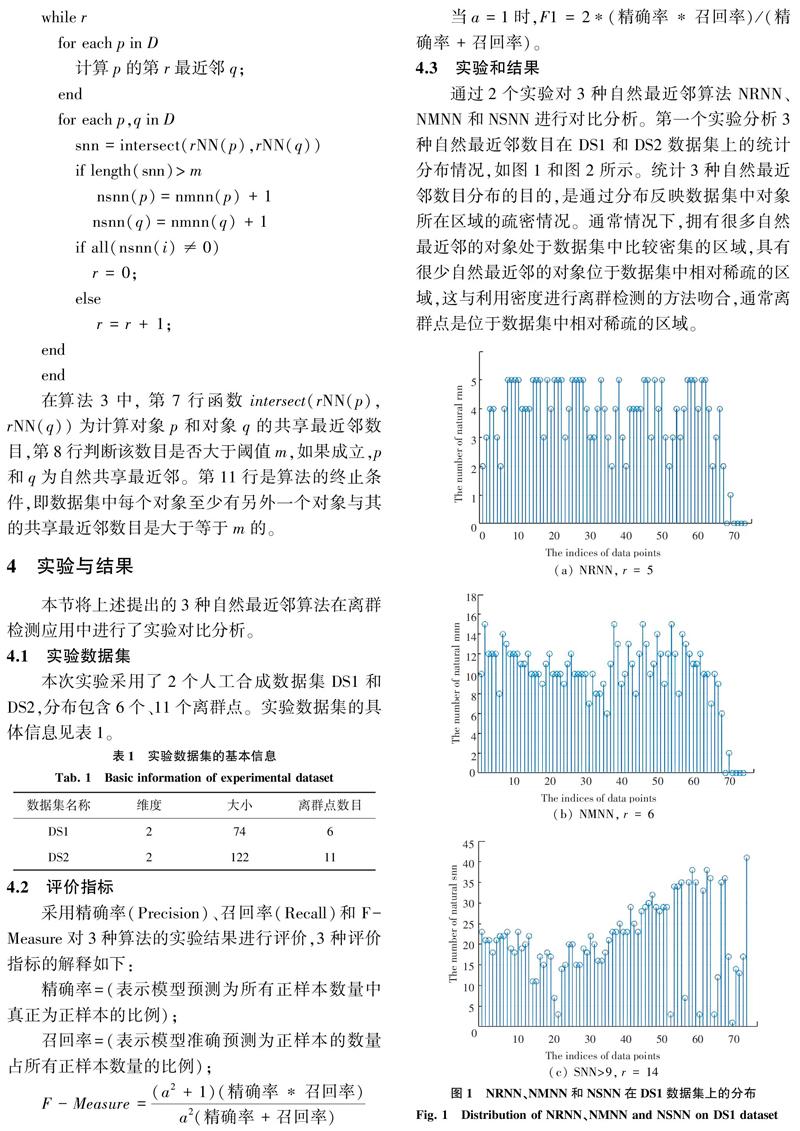
初始化变量r=1，向量nrnn（i）=0，0

while r

for each p in D

计算p的第r最近邻q;

nrnn（q）=nrnn（q）+1;

if all（nrnn（i）≠0）

r = 0;

else

r=r+1

end

在算法1中，第5行给出了算法的终止条件，即数据集D中的每个对象都至少有一个逆最近邻。在实际应用中，对于包含一些相对离群对象的数据集，算法的收敛性变的很差。因此，在算法的具体实现中，加入了另外一个终止条件，即在迭代过程中数据集中没有逆最近邻的数据对象的数目连续两次没有变化，则算法停止。该终止条件对算法的本质并没有影响，因为算法的目的是统计数据集中对象的逆最近邻数目，逆最近邻数目反映了数据对象的密度分布信息。算法提前终止说明数据集中的一些对象处于相对稀疏的区域，这对数据集整体的密度分布并没有影响。在下面2个算法的具体实现中，也加入了类似的终止条件。

算法2 自然互最近邻算法（NMNN）

输入：数据集D包含n个对象

输出：D中每个对象的自然互最近邻数目

算法描述如下：

初始化变量r=1，向量nmnn（i）=0，0

while r

for each p in D

计算p的第r最近邻q;

end

for each p，q in D

if ismember（p，rNN（q）） and ismember（q，rNN（p））

nmnn（p）=nmnn（p）+1

nmnn（q）=nmnn（q）+1

if all（nmnn（i）≠0）

r = 0;

else

r = r + 1;

end

end

在算法2中，第7行的if条件中函数ismember（p，rNN（q））表示对象p是对象q的r最近邻，函数ismember（q，rNN（p））表示q是p的r最近邻，当这2个条件同时成立，p和q为互最近邻。第10行是算法的终止条件，即数据集中的每个对象都至少有一个互最近邻。

算法3 自然共享最近邻算法（NSNN）

输入：数据集D包含n个对象

输出：D中每个对象的自然共享最近邻数目

初始化变量r=m，向量nsnn（i）=0，0

while r

for each p in D

计算p的第r最近邻q;

end

for each p，q in D

snn=intersect（rNN（p），rNN（q））

if length（snn）>m

nsnn（p）=nmnn（p）+1

nsnn（q）=nmnn（q）+1

if all（nsnn（i）≠0）

r = 0;

else

r = r + 1;

end

end

在算法3中，第7行函数intersect（rNN（p），rNN（q））为计算对象p和对象q的共享最近邻数目，第8行判断该数目是否大于阈值m，如果成立，p和q为自然共享最近邻。第11行是算法的终止条件，即数据集中每个对象至少有另外一个对象与其的共享最近邻数目是大于等于m的。

4 实验与结果

本节将上述提出的3种自然最近鄰算法在离群检测应用中进行了实验对比分析。

4.1 实验数据集

本次实验采用了2个人工合成数据集DS1和DS2，分布包含6个、11个离群点。实验数据集的具体信息见表1。

4.2 评价指标

采用精确率（Precision）、召回率（Recall）和F-Measure对3种算法的实验结果进行评价，3种评价指标的解释如下：

精确率=（表示模型预测为所有正样本数量中真正为正样本的比例）;

召回率=（表示模型准确预测为正样本的数量占所有正样本数量的比例）;

F-Measure =（a2+1）（精确率*召回率）a2（精确率+召回率）

当a=1时，F1 = 2*（精确率*召回率）/（精确率+召回率）。

4.3 实验和结果

通过2个实验对3种自然最近邻算法NRNN、NMNN和NSNN进行对比分析。第一个实验分析3种自然最近邻数目在DS1和DS2数据集上的统计分布情况，如图1和图2所示。统计3种自然最近邻数目分布的目的，是通过分布反映数据集中对象所在区域的疏密情况。通常情况下，拥有很多自然最近邻的对象处于数据集中比较密集的区域，具有很少自然最近邻的对象位于数据集中相对稀疏的区域，这与利用密度进行离群检测的方法吻合，通常离群点是位于数据集中相对稀疏的区域。

图1显示了NRNN、NMNN和NSNN在DS1数据集上的统计分布。由此可以看出，当r值为5时，NRNN算法收敛，此时DS1中不是每个数据对象都至少有一个自然逆最近邻。算法收敛是因为在连续2次迭代的过程中，没有自然逆最近邻的对象数目没有变化。同理，在r值为6时，NMNN算法收敛。NSNN算法设置的共享最近邻数目阈值为9，当r值为14时，DS1中每个对象都至少有一个自然共享最近邻。

图2显示了NRNN、NMNN和NSNN 3种算法在DS2数据集上的统计分布。可以看出，NRNN算法在r=6时收敛，收敛时，数据集中仍有几个对象没有自然逆最近邻。当r取值为9时，NMNN算法收敛，此时数据集中的所有对象都至少有一个自然互最近邻。对于NSNN算法，共享最近邻数目阈值设置为9，当r值为15时，NSNN算法收敛，此时，数据集中仍有几个对象没有自然共享最近邻。

离群点通常处于数据集中稀疏的区域，根据自然最近邻数目在数据集上的分布，通过设置阈值找到拥有相对少的自然最近邻数目的对象，从而实现离群检测。实验对比结果见表2和表3。

从表2可以看出， NRNN和NMNN能够取得100%的精确率和召回率，NRNN在阈值小于2时，F1指标为100%，NMNN在阈值小于5时，F1指标为100%。通过整体对比，NRNN略优于NMNN。NSNN在精确率、召回率和F1指标上的结果都相对比较低。

分析表3得出，NMNN在阈值小于17时，取得了100%的精确率和召回率，整体来看，NMNN略优于NRNN。NSNN在阈值小于5时，取得了100%的精确率，但只有27.3%的召回率，说明挖掘出的离群点很少。NSNN阈值小于11时，取得了81.8%的召回率。

总体来看，NMNN和NRNN在离群检测应用中取得了比较好的效果，NSNN在DS2数据集上可以实现离群检测，但在DS1数据集上表现不太理想，这与数据集中数据分布的相对密度有关。NRNN倾向于发现处于稀疏区域和处于数据集外边缘的对象，NMNN能够发现位于稀疏区域和数据集内边缘的对象，NSNN检测出的数据对象相对比较集中。

5 结束语

本文从概念上对目前存在的近邻技术进行了对比分析，对各种近邻技术的特点进行了剖析。结合自然最近邻概念，提出了自然逆最近邻、自然互最近邻和自然共享最近邻3种算法，并给出了3种算法的定义和算法描述。对提出的算法在离群检测应用中进行了实验对比，实验结果表明自然逆最近邻和自然互最近邻能够有效地检测出局部和全局离群点，自然共享最近邻与数据集中数据的相对分布密度有关，检测出的对象相对比较集中。

参考文献

[1]毋雪雁， 王水花， 张煜东. K最近邻算法理论与应用综述[J]. 计算机工程与应用， 2017， 53（21）：1-7.

[2]黄文明， 莫阳. 基于文本加权KNN算法的中文垃圾短信过滤[J]. 计算机工程， 2017， 43（3）：193-199.

[3]张旭， 蒋建国， 洪日昌， 等. 基于朴素贝叶斯K近邻的快速图像分类算法[J]. 北京航空航天大学学报， 2015， 41（2）：302-310.

[4]管建， 亚娟， 王立功. K近邻分类指导的区域迭代图割算法研究[J]. 计算机应用与软件，2018，35（11）：237- 244，265.

[5]卢伟胜， 郭躬德， 严宣辉， 等. SMwKnn：基于类别子空间距离加权的互k近邻算法[J]. 计算机科学， 2014， 41（2）：166-169.

[6]苏晓珂， 郑远攀， 萬仁霞. 基于共享最近邻的离群检测算法[J]. 计算机应用研究， 2012， 29（7）：2426-2428，2453.

[7]KORN F， MUTHUKRISHNAN S. Influence sets based on reverse nearest neighbor queries [J]. ACM SIGMOD Record， 2000， 29（2）：201-212.

[8]GAO Yunjun， LIU Qing， MIAO Xiaoye， et al. Reverse k -nearest neighbor search in the presence of obstacles[J]. Information Sciences， 2016， 330：274-292.

[9]邹咸林. 自然最近邻居在高维数据结构学习中的应用[D]. 重庆：重庆大学， 2011.

[10]朱庆生， 唐汇， 冯骥. 一种基于自然最近邻的离群检测算法[J]. 计算机科学， 2014， 41（3）：276-278， 305.