空谱特征分层融合的高光谱图像特征提取

姚本佐， 何芳

(1.安徽公安职业学院，合肥 230088； 2.火箭军工程大学核工程学院，西安 710025)

0 引言

高光谱图像是由二维空间维和一维光谱维组成的“空谱合一”的超维数据[1-3]。将不同时期高光谱图像上的地形地貌以及目标变化作为一种有效的探测手段，在军事侦察和公安战术指挥等领域发挥了重要的作用[4-7]。然而，高光谱图像具有的较高数据维数也为高光谱图像处理带来了巨大的挑战，具体表现在，数据的存储与传输需要性能更高的计算平台； 数据处理的复杂性增加，处理效率降低[8]。降维方法可以有效解决上述问题，实现数据的维数约减，从而降低数据处理的复杂性。根据实现方法的不同，降维可以分为特征提取及特征选择2大类。

高光谱图像特征提取方法众多[9-11]。常用的方法有： 主成分分析(principal component analysis，PCA)、无监督判别投影(unsupervised discriminant projection，UDP)、局部保持投影(locility preserving projection，LPP)算法和近邻保持嵌入(neighborhood preserving embeding，NPE)算法。然而，这些方法仅利用了高光谱图像的光谱特征，并没有充分利用高光谱图像的空间特征。Li等[12]利用多特征融合方法提出了一种新的高光谱图像分类框架，可以处理高光谱数据线性和非线性的类边界问题。基于此，本文设计了分层融合框架，利用基于光谱维的特征提取方法学习样本的判别特征，通过多尺度自适应加权滤波器(adaptive weighted filters，AWF)迭代更新样本的近邻区域，提取样本的多尺度空间特征，减小样本的类内差异性，使得到的分类结果更加平滑。在此基础上，将无监督降维算法PCA融合到分层融合框架中，进一步提出了分层融合-主成分分析(hierarchical fusion-principal component analysis，HF-PCA)算法。首先，利用PCA算法将原始高光谱图像降维，减小波段间的冗余性； 然后，对降维后的数据采用多尺度AWF滤波，将每一个尺度上得到的滤波结果作为一层新的空谱特征，再将所有特征融合为新的图像； 最后，采用K最近邻(K-nearest neighbor，KNN)分类器进行分类。

1 空谱特征分层融合学习方法

1.1 基于AWF的空间特征学习方法

AWF是一种空间滤波器，可以提取高光谱图像的空间信息。图1为3×3的AWF示意图。

图1 AWF示意图Fig.1 Adaptive weighted filters

图1中第i行第j列像元点的自适应权重为

(1)

(2)

式中：l为滤波器的尺寸；sij为相似度衡量指标；p0为滤波器中心位置的像素值；pij为该区域中第i行第j列的像素值;σ的计算公式为

(3)

d(i-1)×l+j=‖p0-pij‖2。

(4)

从图1可以看出，在AWF中不同位置的权重不同。中心像元点的权重可以通过对其邻近像元的权重进行加权求和得到。

1.2 PCA

PCA是一种经典的特征提取算法，作为一种预处理手段，在高光谱图像处理中也具有重要的应用。设高光谱数据集为X=[x1,x2,…,xN]∈RN×D，其中，N为每个波段上像元的个数，D为所有波段的个数，则矩阵X的均值μ为

(5)

此外，矩阵X的协方差矩阵S为

(6)

采用特征值分解的方法可得到S的特征值和特征向量为

Swi=λiwi,i=1,2,…,N，

(7)

式中λi为特征向量wi对应的特征值。将特征值λi按从大到小的顺序进行排列，从中选取前k个较大的特征值对应的特征向量组合成高光谱图像的特征空间，即{w1,w2,...,wk}。

降维后的数据yi是将经过去均值化处理的数据映射到该特征空间中，即

yi=wT(xi-μ)。

(8)

1.3 基于PCA与AWF分层融合的学习方法

PCA利用最小均方根误差准则和二阶统计方法为样本点寻找一个最佳的投影方向，使投影后得到的数据间的方差最小，能够提取出高光谱图像中的重要光谱特征，降低维数，减小数据量。本文提出PCA与AWF分层融合的HF-PCA算法，首先，采用PCA算法将高光谱图像降维，获取其低维光谱特征； 然后，采用多尺度AWF在光谱特征上进行空间滤波，平滑降维后的图像，增大同类样本间的相似性，有利于高光谱图像的分类。HF-PCA算法具体步骤如下： ①在光谱维上，采用PCA算法将原始高光谱图像降到n维； ②在空间维上，对获得的光谱特征数据分别采用不同尺度的AWF进行滤波，得到空谱Map1，Map2，…，Mapk； ③将得到的所有空谱Map图融合为n×k的多层Map图； ④重复步骤②和③m次，得到经过m次融合后的空谱图像； ⑤采用KNN分类器对融合后的数据进行分类。HF-PCA算法框架如图2所示，图2中AWF-Sk表示采用第k个尺度的自适应加权滤波器。

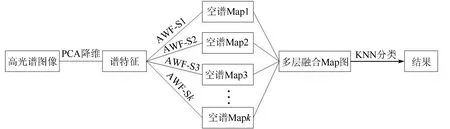
图2 单次HF-PCA算法框架Fig.2 Frame of HF-PCA

2 实验验证与结果分析

2.1 实验数据

选择具有代表性的Indian Pine[13]和Salinas[14]图像用于验证本文所提算法的有效性。Indian Pines图像是1992年6月由AVIRIS传感器在美国印第安纳州的一块印度松树测试地获取的。该图像大小为145像元×145像元，去除水汽吸收及噪声剩下200个波段用于实验。图像上含有16类不同的地物类型。图3(a)为Indian Pines B50(R)，B27(G)，B17(B)假彩色合成影像，图3(b)为其地面真实数据，图例中数值为样本个数。

(a) B50(R)，B27(G)，B17(B) (b) 地面真实数据假彩色合成影像

图3 Indian Pines图像

Fig.3IndianPineshyperspectralimage

Salinas图像是由AVIRIS传感器在加利福尼亚州萨利纳斯山谷获得的，数据空间分辨率为3.7 m，图像大小为512像元×217像元，包含224个波段，去除20个被污染波段后，剩下204个波段用于实验。图像上共含有16类不同的地物类型。图4(a)为选取Salinas B16(R)，B130(G)，B200(B)假彩色合成影像，图4(b)为其地面真实数据，图例中数值为样本个数。

(a) B16(R)，B130(G)，(b) 地面真实数据B200(B)假彩色合成影像

图4 Salinas图像

Fig.4Salinashyperspectralimage

2.2 实验方法

首先，采用PCA和HF-PCA算法对高光谱图像进行降维； 然后，采用KNN分类器对降维后的数据进行分类。将不做降维处理直接进行分类的结果作为基准线(baseline)。利用高光谱图像的分类精度评价指标： 总体精度(overall accuracy，OA)、平均精度(average accuracy，AA)和Kappa系数衡量各个算法的分类性能[13]。OA，AA和Kappa系数越高表明该方法对高光谱图像的分类效果越好。

2.3 基于Indian Pines数据库的高光谱图像分类

从Indian Pines数据库中随机选取每类样本的5%作为训练样本，样本数不足100时选取10个，剩下的所有样本作为测试样本。将每种算法重复进行5次分类实验，取5次OA和Kappa系数的均值作为最终的分类结果。设置HF-PCA算法初始降到的维数为15，融合次数m为3，多尺度AWF滤波器的尺度为5，每个尺度上的窗口分别为3×3，5×5，7×7，9×9，11×11。设定所有降维算法降到的维数为15，训练样本选取每类地物样本的5%(样本数不足100时选10个)时，由不同算法获得的地物分类结果如图5所示，各类地物的分类精度如表1所示。

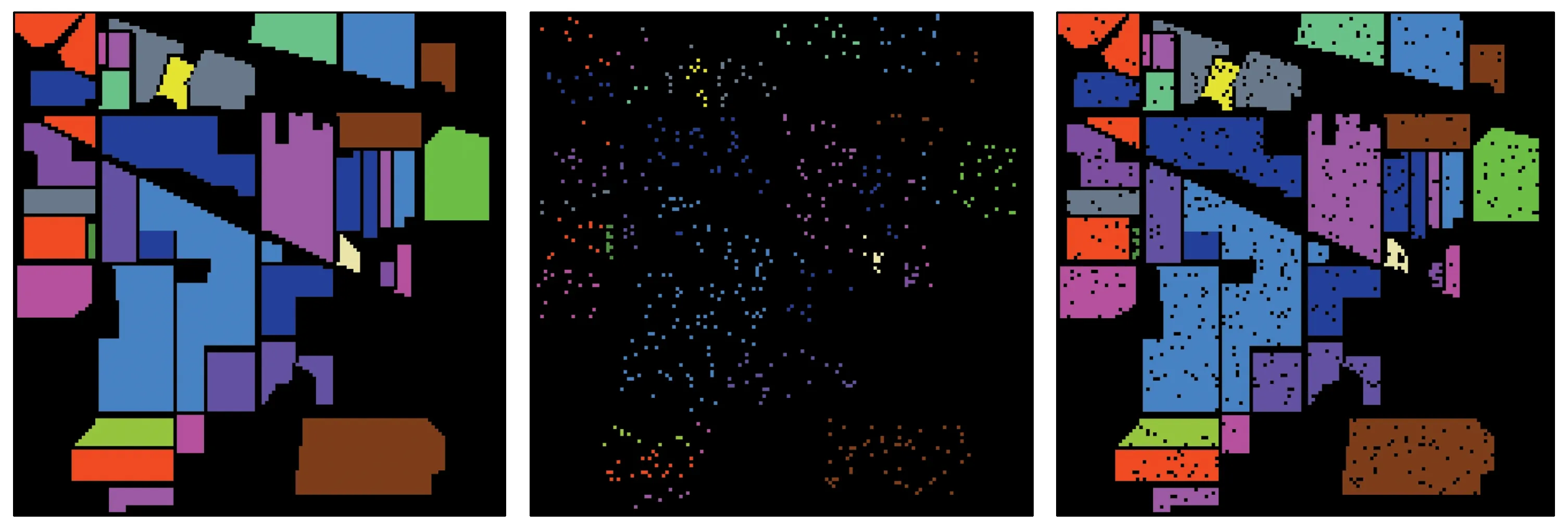
(a) 真实地物图 (b) 训练样本 (c) 测试样本

(d) baseline (e) PCA (f) HF-PCA

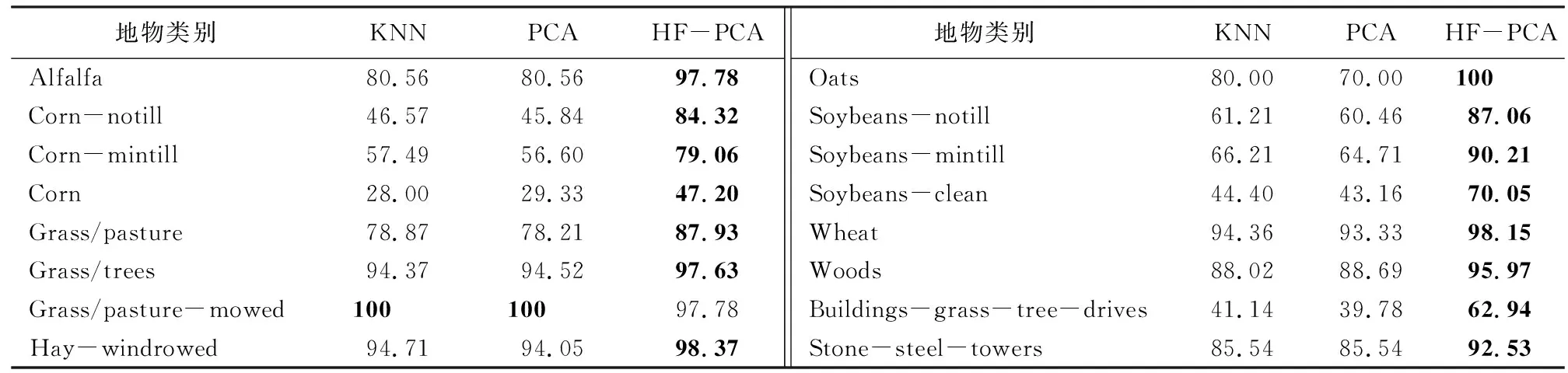
图5 Indian Pines数据库各算法的分类结果Fig.5 Classification results of different algorithms in Indian Pines dataset表1 Indian Pines数据库不同算法各类地物的分类精度Tab.1 Classification accuracy of different types of features in Indian Pines dataset by different algorithms (%)

由图5可知，由HF-PCA算法得到的地物分类结果更加平滑，错分或漏分现象明显减小。进一步由表1的定量分析可知，HF-PCA算法对大多数地物的分类精度均有显著提高，除Grass/pasture-mowed地物外，其他15类地物的分类结果均显著高于其他算法。造成这种现象的原因可能是因为在分层融合的时候只是单纯地将光谱特征进行叠加，没有考虑高光谱图像样本的分布特点，高光谱数据在空间上具有分布一致性特点，即相邻样本点属于同一类的概率较大。HF-PCA算法从全局考虑提升样本的OA和Kappa系数，忽视了高光谱样本的局部特性，因此，在后续工作中，可以考虑结合高光谱图像的局部分布特点和全局特性提出更加有效的高光谱图像处理算法。就整体而言，HF-PCA算法得到的OA为86.73%，分别比KNN和PCA的结果高出了20.04%和20.74%； 得到的Kappa系数为0.848 4，分别比KNN和PCA的结果提高了0.229 5和0.237 4。这是由于HF-PCA算法引入分层融合的方法获取高光谱图像的不同空间结构，将其与降维后的光谱特征进行融合学习，分层融合的空谱特征既降低了信息的冗余度，又增加了同类样本的相似性，增强了样本的可分性，有利于高光谱图像的分类，对于小样本的分类仍然具有优越性。

2.4 基于Salinas数据库的高光谱图像分类

在Salinas数据库上进行同样的实验，选取每类地物样本的1%作为训练样本，其余所有样本作为测试样本。将各种降维算法降到10维，融合次数m设为3，设置HF-PCA算法中的多尺度AWF滤波器的尺度为5，每个尺度上的窗口分别为3×3，5×5，7×7，9×9，11×11。在训练样本相同的情况下，由不同算法获得的地物分类结果如图6所示，各类地物的分类精度如表2所示。

(a) 真实地物 (b) 训练样本 (c) 测试样本 (d) baseline (e) PCA (f) HF-PCA

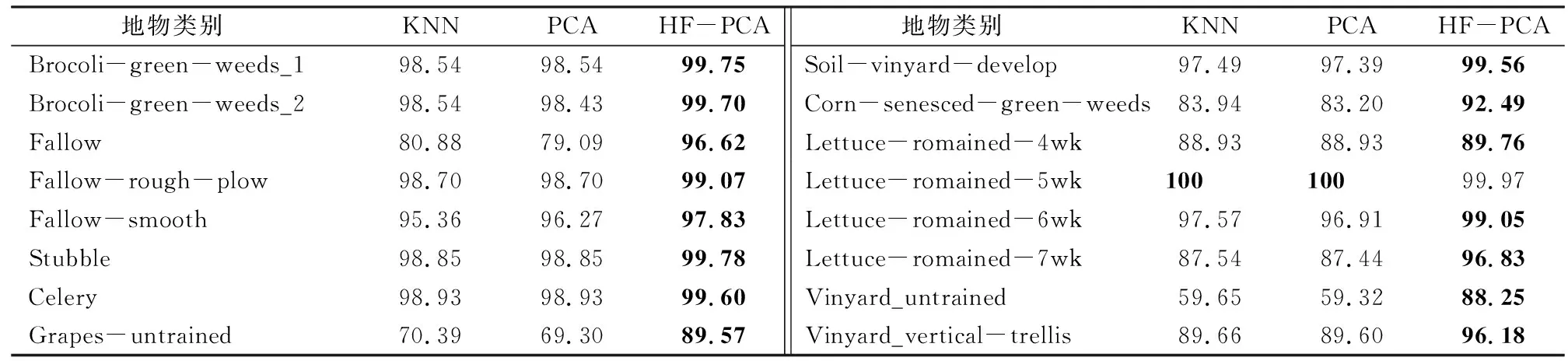
图6 Salinas数据库各算法分类结果Fig.6 Classification results of different algorithms in Salinas dataset表2 Salinas数据库不同算法各类地物的分类精度Tab.2 Classification accuracy of different types of features in Salinas dataset by different algorithms (%)

由图6可知，由HF-PCA算法得到的地物分类结果更加平滑，地物的分布更加清晰，这是由于HF-PCA算法利用了高光谱图像的空间结构信息，比单纯地利用高光谱的光谱信息实现降维分类具有明显的优势。进一步由表2的分析可知，HF-PCA算法对大多数地物的分类精度均有显著提高。由HF-PCA算法得到的OA为95.01%，分别比KNN和PCA的结果高出了9.98%和10.34%； 得到的Kappa系数为0.944 5，分别比KNN和PCA的结果高出了0.111 2和0.115 2，再次证明了分层融合空谱特征提取方法的有效性。

3 结论及展望

针对高光谱图像中维数较高，数据间的冗余性较大的问题，本文提出了分层融合-主成分分析(HF-PCA)算法，该算法有效提高了高光谱图像的分类精度。主要结论为：

1)设计了分层融合框架，有效提取了高光谱图像中重要的空谱特征，从而提高分类精度。

2)将PCA算法融入到分层融合框架中，提出了HF-PCA算法，不仅降低了波段间的冗余性，而且削弱了样本的类内差异性，显著提高了高光谱图像的分类精度。

3)实验结果表明，即使在训练样本数量较少的情况下，由HF-PCA算法得到的分类精度明显高于其他算法。

然而，本文所提算法从全局角度提升样本的总体分类精度和Kappa系数，但忽视了高光谱样本的局部特性。因此，在后续工作中，将考虑结合高光谱图像的局部分布特点和全局特性，提出更加有效的高光谱图像处理算法。