融入边界特征的遥感影像多尺度分割

2019-09-12翟德超范亚男周亚男

自然资源遥感 2019年3期

翟德超，范亚男，周亚男

(1.中国科学院大学地理科学与资源研究所，北京 100020； 2.河海大学地理信息科学系，南京 211100； 3.天津市测绘院，天津 300381)

0 引言

面向对象的遥感影像分析方法能够在利用地物光谱特征的基础上，进一步挖掘地物几何、纹理和边界等空间特征，并结合影像场景丰富的空间关系和上下文特征，使得对影像的分析和理解更加合理有效[1]。面向对象的影像信息提取首先需要对影像进行多尺度分割，形成具有一定光谱、形状特征的影像基元(即一定尺度下，特征相似的像元组成的连通区域构成影像视觉上的基本单元[2])。多尺度分割是面向对象的“像元—基元—目标—格局”[3]影像分析计算的基础，而影像本身的多波段、地物类型多样和场景复杂等特性，使得影像多尺度分割成为面向对象影像分析中最具不确定性的环节[4]。

目前提出的影像多尺度分割方法(如分形网络演化方法(fractal net evolution approach, FNEA)[5-6]、均值漂移算法[7-8]、基于加权聚合的分割方法(segmentation by weighted aggregation, SWA)[9-10]、图割算法[11]和隐马尔科夫树分割算法(hidden Markov tree, HMTseg)[12-13]等)均源于自底向上的区域合并理论，依据相邻基元的相似性度量决定相邻基元是否合并及其合并顺序，不断合并小尺度基元形成大尺度基元，实现多尺度分割。如FNEA和均值漂移算法以基元的光谱特征和形状特征的相似度的加权和作为基元的同质性度量； SWA和图割算法则利用基元的光谱特征和纹理特征度量基元的相似性，表达连接权重。上述方法仅考虑基元自身的光谱、形状和纹理等内在的区域特征，忽略了对相邻基元间公共边界特征的分析和运用。高空间分辨率影像含有丰富的边界信息，不同于光谱、形状和纹理等特征是基元区域内像素的光谱和局部空间分布信息的量化统计，边界特征表达基元相互分离的程度，是基元差异性的表现，是地物空间关系的重要特征。在基于像素的影像分割中，通常先提取影像的边界，然后用边界拟合[14]、感知分组和悬挂连接等后处理方法来连接边界点成闭合线，实现影像分割。这类方法较多，但后处理复杂且难以生成完整的分割基元。然而在面向对象的影像多尺度分割方法中，对基元边界特征的分析和应用较少。

本文从影像的边界出发，分析和提取相邻基元间公共边界的多种特征，具体包括：公共边界上的梯度强度、梯度方向特征，公共边界占基元边界总长度的比例信息；并将这些特征引入SWA方法[9,15]中，同基元区域特征相融合，优化基元间的相似度计算，构建了融入边界特征的多尺度加权聚合遥感影像分割方法(edge-incorporated multi-scale image segmentation by weighted aggregation,EIMSSWA)，旨在提高影像的分割精度。

1 EIMSSWA方法

在自底向上的影像分割过程中，相邻基元间公共边界是基元间特征相似度的重要影响因子，关系到基元的合并过程。EIMSSWA方法在提取影像边界信息基础上，分析相邻基元间公共边界的比率、强度均值、强度方差和方向方差特征，并将其同基元区域特征相似度相融合，优化相似性度量，提高遥感影像多尺度分割的精度。

1.1 EIMSSWA方法分割流程

基于图割理论的影像分割模型源于谱图划分，其将影像分割看成一个无向加权图的多路划分问题。首先将影像映射为带权无向图，然后以某种准则构造图的最小割的代价函数，继而迭代划分加权图，使得代价函数最小(所求划分的集合间相似度最小，集合内相似度最大)，实现最优分割。由于图划分测度的最优解为非确定多项式(non-deterministic polynomial, NP)的困难问题[16-17]，Sharon等[9,15]将多重网格解法(algebraic multigrid solution, AMG)的加权聚合规则引入到基于图割的影像分割方法中，提出SWA影像分割算法：将在细尺度图上寻找影像最优图割的问题逐步转化到节点数目更少的粗化图上进行，实现影像的快速分割[18]。

本文在上述影像分割方法的基础上，挖掘和分析基元间的边界特征，提出EIMSSWA方法(图1)。

图1 EMISSWA方法流程图Fig.1 Method flowchart of EIMSSWA

具体分割过程如下： ①在全色和多光谱的融合影像上，以像素为顶点，以相邻像素间光谱特征的相似度(光谱向量的相关系数)为连接权重，建立像素的四邻域加权邻接图(尺度为1)； ②对尺度为s的邻接图的节点按节点度由大到小排序，并选取一定数目的节点作为种子点(同时也是下一尺度s+1邻接图的顶点)； ③根据尺度间内插矩阵，计算非种子节点到相邻种子节点的归属度，并将非种子点聚类到以种子点为中心的集合中(s尺度的邻接图中，一个集合中的所有顶点构成了s+1尺度邻接图的一个顶点)，构建s+1尺度的邻接图； ④计算s+1尺度邻接图中顶点间的连接权重(节点间光谱、纹理、几何、边界等特征相似度)，并评价分割基元的显著性； ⑤重复②—④，直到邻接图节点数为1，最终构建影像的多层分割金字塔； ⑥采用自顶向下的方法，确定聚合区域的边界，形成多尺度分割结果。

有关SWA影像分割的理论和流程，可参见文献[9，15]；本文将重点挖掘影像中丰富的边界信息，提取基元间的边界特征，并将其同基元区域特征相融合(步骤④)中，优化基元相似度计算，提高分割结果精度。

1.2 基元间的边界特征

边界特征是影像分析中除光谱、纹理和几何特征外的重要信息；在影像解译认知过程中，边界是分离和区分相邻地物的重要依据。在自底向上的影像分割过程中，强边界表示基元间相似度较小，其合并的可能性降低；相反，弱边界表示基元间相似度较高，基元间更可能合并。图2为理想情况下的地物分割基元间边界特征分析示意图。

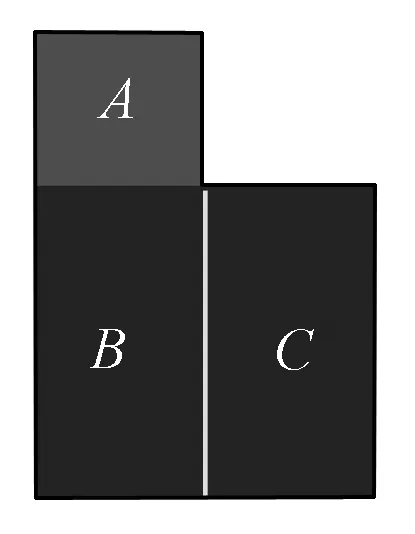
图2 基元间边界特征分析Fig.2 Analysis of edge between primitives

如图2所示，A，B和C为某一尺度下的分割基元，其中基元B和C的光谱和几何特征非常相似，基元A和B的光谱和几何特征差异稍大；因此基元A和B间的光谱、几何相似度均小于基元B和C间的光谱、几何相似度。若仅考虑由光谱和形状特征所构建的基元间相似性度量，则由于基元A和B的相似度小于基元B和C的相似度，基元B和C将优先合并。然而基元B和C间的公共边界更明显、强度更大，极大地降低了基元间的相似度；而基元A和B间的公共边界较弱、强度较小，相似度受边界特征影响相对较小。边界特征的融入将使基元A和B的相似度大于基元B和C的相似度，基元A和B优先合并，得到更好的分割结果。

上述分析直观地阐述了基元间边界特征在影像多尺度分割中的重要作用。由于Sobel算子具有平滑噪声、提取边缘方向精确和计算简单的优点，本文首先运用纵横双向Sobel边缘检测算子[19]对实验区全色影像进行边界检测，计算影像区域的梯度强度和梯度方向；然后分析基元间公共边界上的梯度强度和梯度方向分布，并提取边界比率、强度均值、强度方差和方向方差等边界特征。

1.2.1 边界梯度特征

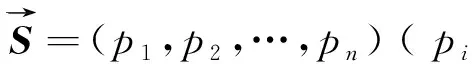
(1)

(2)

(3)

(4)

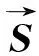
1.2.2 边界比率特征

(5)

(6)

RB=min(RB1，RB2)。

(7)

1.3 边界特征的相似度

在提取边界特征的基础上，进一步讨论如何将边界特征IE，ID，DD和RB融入到相邻基元间的相似度度量中。

设相邻基元Bi和Bj的边界特征，梯度强度均值、梯度强度方差、梯度方向方差和协调边界比率分别为IE，ID，DD和RB；由1.2节对各特征的分析，相邻基元间的边界特征与IE正相关，与ID，DD和RB负相关。为此构造边界特征因子FCE，即

(8)

式中π用于消除角度量纲，使FCE为无量纲因子。

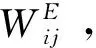
(9)

式中t>0为边界影响权重调节因子，用于调节边界特征对基元相似度的影响程度。t增大，边界特征对基元间相似度的影响变小；t减小，边界特征对基元间相似度的影响增大。

由于边界特征的融入，优化了基元间的相似度度量；基元间的合并方式和合并顺序得到了优化调整，从而能提高影像分割结果的精度。

2 实验及分析

为验证EIMSSWA方法的合理性和有效性，设计以下分组对比实验： ①基于eCognition软件的多尺度分割实验(以下代称FNEA)； ②SWA多尺度分割实验； ③EIMSSWA多尺度分割实验。选取武汉市城区部分区域的QuickBird全色影像和多光谱影像数据，采用Gram-Schmidt方法[15]生成全色和多光谱融合影像(图3)并对其进行多尺度分割实验。有关FNEA和SWA方法的流程可参见文献[9,15,20]，这里仅对必要的实验流程进行说明。

(a) 全色影像 (b) 融合影像(B4(R),B3(G),B2(B)假彩色合成)

图3 实验区影像

Fig.3Satelliteimageofexperimentarea

2.1 FNEA多尺度分割实验

利用eCognition8.0软件进行影像FNEA多尺度分割。根据实验影像的区域特点和地物(主要是建筑物)特征属性，设计了FNEA的多尺度分割策略。考虑到影像中建筑物多为矩形，形状特征较强，设置分割的形状因子为0.3，紧致度因子为0.5；由经验法获得相应的参数数值，构建10，20，40和200共4个尺度层次。当尺度为10时，分割得到地物单元层，形成琐碎的地物分割单元；当尺度为20时，得到建筑物基元层，大部分建筑物基元被分割出来；当尺度为40时，得到建筑群基元层，建筑物全部分割出来，小部分建筑物基元出现合并；尺度为200时，得到区域格局层，生成区域的大尺度格局分割。

2.2 SWA多尺度分割实验

参考文献[18]，SWA多尺度分割实验中选取的各个参数分别为：初始化光谱因子c=10，更新光谱因子α=6，纹理因子β=1.0，权重内插矩阵最小权重q=0.1，块选择阈值r=0.2，最大子基元数目u=25，显著性阈值b=0.2。虽然实验中参数设置较多，但这对不同的遥感影像具有很好的稳健性[18]。运用SWA方法对实验区域进行多尺度分割，得到地物单元层、建筑物基元层、建筑群基元层和区域格局层，并同FNEA实验分割结果的对应尺度层对照。

2.3 EIMSSWA多尺度分割实验

EIMSSWA方法将影像边界特征融入到基元相似度计算中，改善影像多尺度分割结果，具体参照1.1节中EIMSSWA方法分割流程。为更好地进行多组实验间的对比，实验中边界特征权重调节因子设为t=5 (t越大，边界特征对基元间相似度的影响越小，反之亦然；经多次实验，当t∈[4,8]分割结果较好)，其他参数与SWA实验参数相同。得到地物单元层、建筑物基元层、建筑群基元层和区域格局层等分割层次，并同上述2组实验结果进行对比分析。

2.4 实验结果与分析评价

图4为3组实验的多尺度分割结果。

(a) FNEA地物单元层(b) SWA地物单元层 (c) EIMSSWA地物单元层

(d) FNEA建筑物基元层(e) SWA建筑物基元层(f) EIMSSWA建筑物基元层

图4-1 3组实验的多尺度分割结果

Fig.4-1Multi-scalesegmentationsofthreeexperiments

(g) FNEA建筑群基元层(h) SWA建筑群基元层 (i) EIMSSWA建筑群基元层

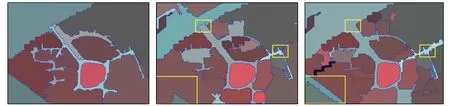
(j) FNEA区域格局层(k) SWA区域格局层 (l) EIMSSWA区域格局层

图4-2 3组实验的多尺度分割结果

Fig.4-2Multi-scalesegmentationsofthreeexperiments

为评价EIMSSWA影像多尺度分割算法的有效性和边界特征在多尺度分割中的作用，对3组实验的分割结果进行分析评价。对比图4(a)—(c)发现，由于精细尺度分割主要利用基元的光谱信息，而纹理、几何和边界特征在小尺度下表现较弱，因此3组实验在地物单元层尺度下的分割结果相似，无明显差别；对比图4(d)—(f)，图4(f)中完整建筑物基元的个数均比图4(d)和(e)多，分析基元合并过程，认为主要原因在于同一房顶相邻基元间公共边界(也是房顶的屋脊线)的梯度较小，而房顶基元同周围阴影和绿地间公共边界梯度较大，EIMSSWA方法考虑了基元间的边界特征，从而相对地增强了房顶基元间的相似度，而减弱了房顶基元同其他地物基元间的相似度，调整基于的合并顺序，得到了更合理的分割结果；对比图4(g)—(i)，图4(h)和(i)对实验区右上角黑色建筑物的分割结果均比图4(g)好，得到了更完整的建筑物基元，图4(i)中地物基元独立性比图4(h)好，地物基元同周围不同类地物基元间的错误合并少(黄框区域)；对比图4(j)—(l)，图4(l)在整体格局上分割不及图4(j)好，但其对影像中央道路的格局划分较好(黄框区域)。

为进一步定量说明边界特征融入对多尺度影像分割的效果，本文采用文献[21-22]阐述的影像分割的数值评价方法，通过计算影像分割结果的区域内部非均匀性、区域间对比度和区域间散度对比度等3个参数综合评价分割结果；而对多个尺度的分割结果，则分层次分别计算，并求其平均值。其中区域内部非均匀性用于描述分割结果的质量，非均匀性测度越小，区域内部一致性越好，分割效果越好；区域间对比度表达影像整体的区域对比度，对比度值越大，区域间差异越大，分割效果越好；区域间散度对比度用区域的灰度方差来描述区域间的差异，其值越大，区域间的差异越大，分割效果越好。3组实验的数值评价结果如表1所示。

表1 3组实验结果评价分析Tab.1 Evaluation of three experiments results

分析对比表1中3组实验数值，可以看出：对于多尺度分割得到的每一个分割层次，EIMSSWA方法的分割结果比FNEA方法和SWA方法的分割结果都具有更小的区域内部非均匀性、更大的区域间对比度和更大的区域间散度对比度；多个层次的平均结果依然。融入边界特征的EIMSSWA遥感影像多尺度分割方法具有更高的分割精度，分割效果更好。