通道压裂支撑剂嵌入幂率模型的建立与分析

2019-09-11许国庆杨贤友

岩性油气藏 2019年5期

许国庆，石阳，江昀，杨贤友

（中国石油勘探开发研究院，北京100083）

0 引言

通道压裂技术是近年来提出的一种新型压裂技术，其特点在于通过支撑剂不连续铺置，在裂缝内形成具有高导流能力的网络通道，大幅降低油气渗流阻力，从而提高油气产量［1-2］。与传统压裂工艺相比，通道压裂技术可显著解决由于支撑剂嵌入、破碎、微粒运移以及液体伤害等因素导致的裂缝导流过低的问题［3-5］。

目前针对通道压裂方面的研究主要集中在现场应用和裂缝导流能力影响因素分析方面，包括支撑剂铺置方式、支撑剂类型以及纤维浓度优化等［6-7］，但其中支撑剂嵌入行为的分析主要是针对某些特定储层所进行的导流实验［8］，难以获得一般性认识，且缺乏相应的理论分析，无法推广到常规应用。支撑剂的嵌入行为可导致裂缝开度减小，进而降低裂缝导流能力，影响油井产能，严重时甚至会导致裂缝完全失效［9］。因此准确描述支撑剂嵌入过程对于压裂裂缝导流能评价具有重要意义。

现有的支撑剂嵌入研究以常规压裂方式为主，主要涉及实验研究、数值模拟以及理论推导。其中实验研究针对不同储层类型、支撑剂类型以及支撑剂浓度等因素［10-13］，进行了系统的分析，并将实验结果用于裂缝导流能力优化［14］，指导现场施工。数值模拟以 Cui等［9］和 Song 等［15］为代表，以有限元方法分析了单个支撑剂颗粒嵌入问题。有限元法虽然能够获得支撑剂嵌入过程的定量认识，但难以用于实际工程设计，现场应用仍以理论模型为基础。

理论模型的发展前期以经验和半经验公式［16-20］为主，其中参数的确定依赖于室内实验。后期的发展以Gao等［21］的解析模型最为完善，其以Hertz理论为基础，分析了支撑剂间的球形接触变形以及支撑剂与储层的球面接触变形，最终推导了考虑二者综合变形的导流能力计算公式，但该解析模型在计算过程中没有考虑储层的塑性变形。

针对通道压裂支撑剂嵌入的理论模型，其计算过程仍以Hertz理论为基础，仅考虑弹性变形［22］。以支撑剂支柱为研究对象，不再考虑单个支撑剂的嵌入行为，建立支撑剂嵌入深度计算幂率模型，给出支撑剂嵌入深度的计算方法，并将计算结果与已知模型［17，23］和实验结果［24］进行对比，验证该方法的准确性，并对该计算方法进行影响参数分析，以期达到优化通道压裂设计的目的。

1 模型建立

1.1 支撑剂受力分析

通道压裂技术将支撑剂与纤维混合后，以脉冲的形式泵注到裂缝内，利用纤维与支撑剂间的内聚力在裂缝内形成稳定支柱，创造油气渗流网络通道，从而达到提高油气采收率的目的［1-2］。此时支撑剂支柱不再起到油气渗流媒介的作用，仅发挥支撑裂缝的作用［25］。如图1所示为通道压裂支撑裂缝示意图。

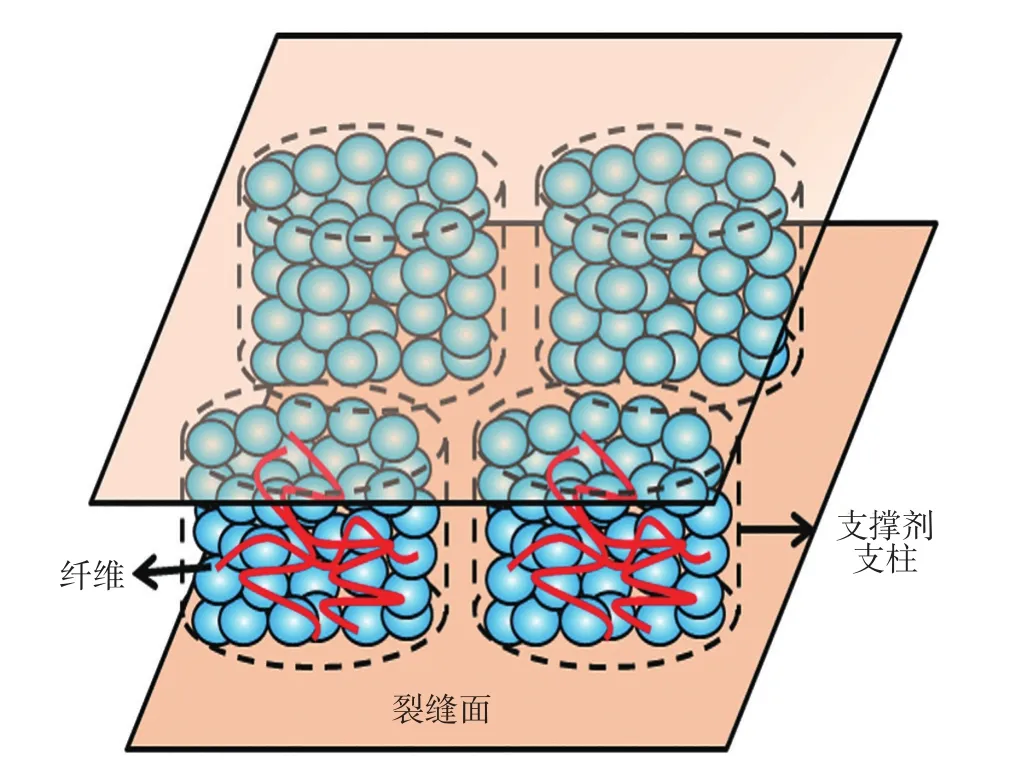
图1 通道压裂支撑剂支柱分布示意图Fig.1 Distribution of proppant pillar in channel fracturing

支撑剂支柱嵌入过程如图2所示。

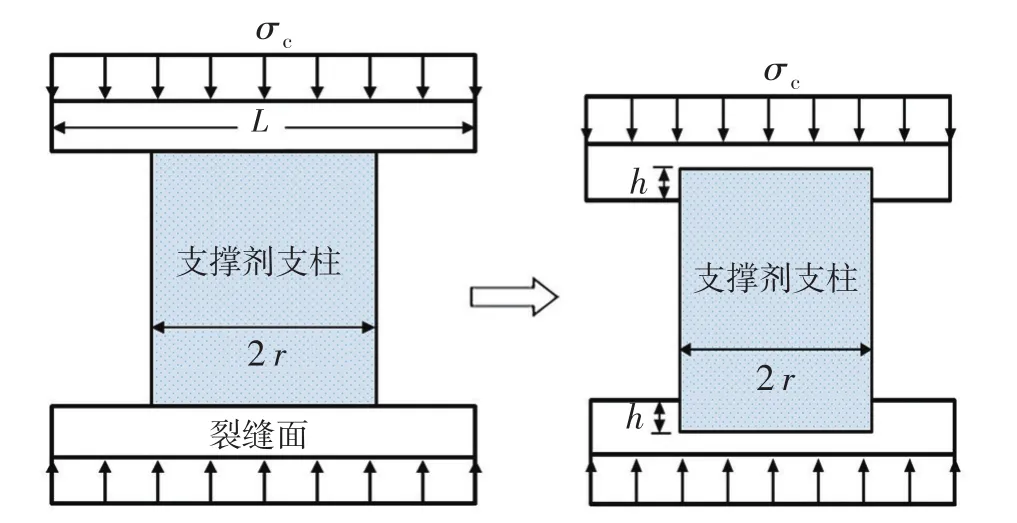
图2 支撑剂支柱嵌入过程示意图Fig.2 Scheme of proppant pillar embedment

裂缝内支撑剂在垂直于裂缝壁面的方向上处于受力平衡状态

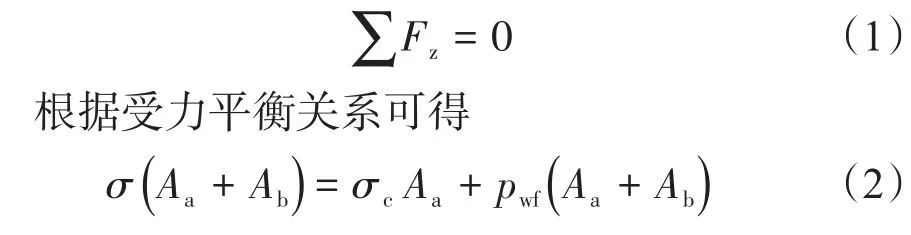
式中：Aa为裂缝内支撑剂铺置面积，m2；Ab为支撑剂未铺置面积，m2；σ 为裂缝闭合压力，MPa；σc为支撑剂承受的有效接触应力，MPa；pwf为裂缝内流体压力，MPa。整理式（2）可得

式中：c为支撑剂铺置面积比；Δ σ = σ -pwf，MPa。

由式（3）可知，支撑剂支柱所承受的接触应力，取决于支撑剂铺置面积比c，在已知裂缝闭合压力和流体孔隙压力的情况下，准确描述铺置面积比c是求取有效接触应力的关键。

1.2 支撑剂嵌入本构模型

常规支撑剂嵌入行为可将其等效为球面接触问题，以 Hertz 理论［22］和 Zener理论［26］较为典型。通道压裂所提供的导流通道以支撑剂支柱间的网络通道为主，支撑剂支柱内部的孔隙对油气流动几乎没有贡献［27］，因此以支撑剂支柱为研究对象，通过力学分析，建立了幂率嵌入模型（图3）。

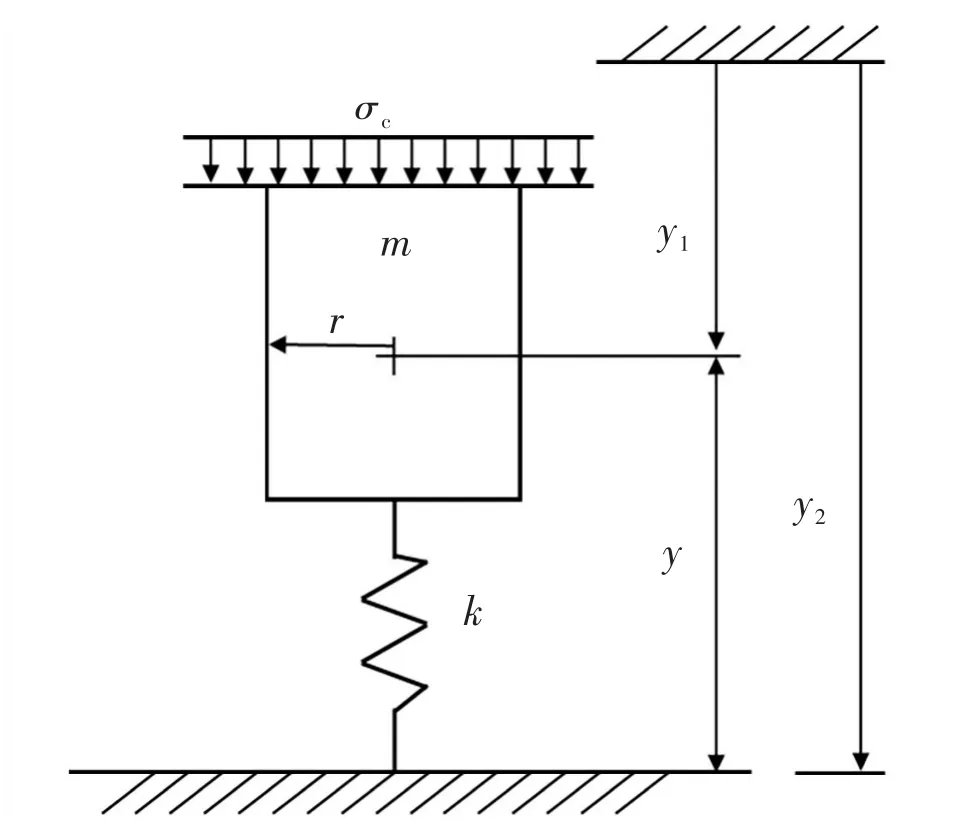
图3 支撑剂支柱嵌入模型示意图Fig.3 Sketch map of proppant pillar embedment

由于通道压裂支撑剂不是连续泵入裂缝，而是以等时脉冲的形式将支撑剂及清水交替泵入裂缝［1-2］，因此支撑剂支柱与岩石的接触面积由脉冲频率决定，但总接触面积不变，即支撑剂支柱所承受的闭合压力不随脉冲频率发生变化。考虑一个直径为2 r，高为h的圆柱体在应力σc的作用下，与岩石发生接触作用，则支撑剂支柱嵌入力可表示为

式中：k为倔强系数，GN·m-n，由储层及支撑剂性质决定；y(t)为嵌入深度，m；n为弹性指数；t为嵌入时间，s。

k与n需实验确定，不同n值对应不同的物理模型。当n取1.5时，表示刚性柱体与光滑弹性半无限平面接触［28］；当n取2时，表示弹性柱体与光滑刚性半无限平面接触［29］。

由受力分析可知

式中：m为支撑剂支柱质量，kg。

由微分变形，式（5）可表示为

式中：v为t时刻的嵌入速度，m/s。

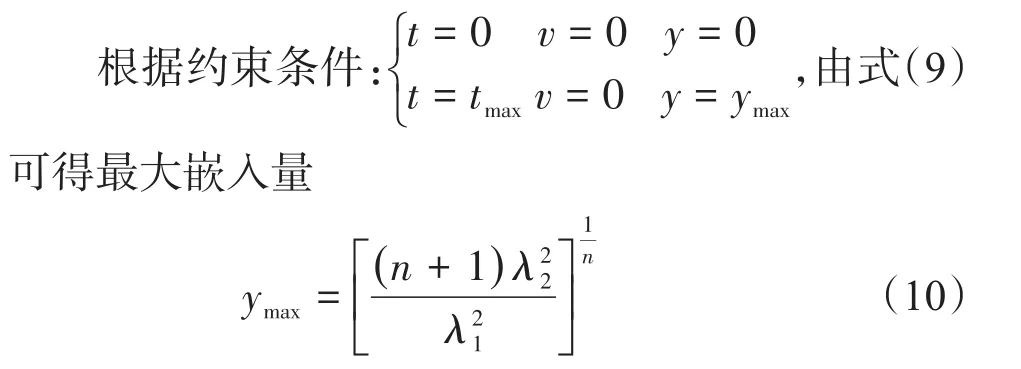
因此确定了相应参数值，即可求得最大嵌入量ymax。其中最大嵌入量包含了支撑剂间的接触变形量。

将式（10）带入式（9）可得

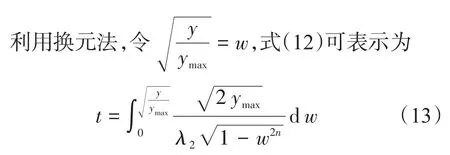
式（13）最后的积分结果可表示为

式中：hypergeom（a，b，z）为高斯超几何方程，可由不同参数值确定最后解的形式。

式（14）为所求的嵌入深度y与嵌入时间t的函数关系，当y=ymax时

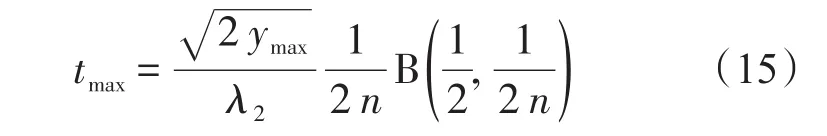
其中 B（a，b）为 Beta函数

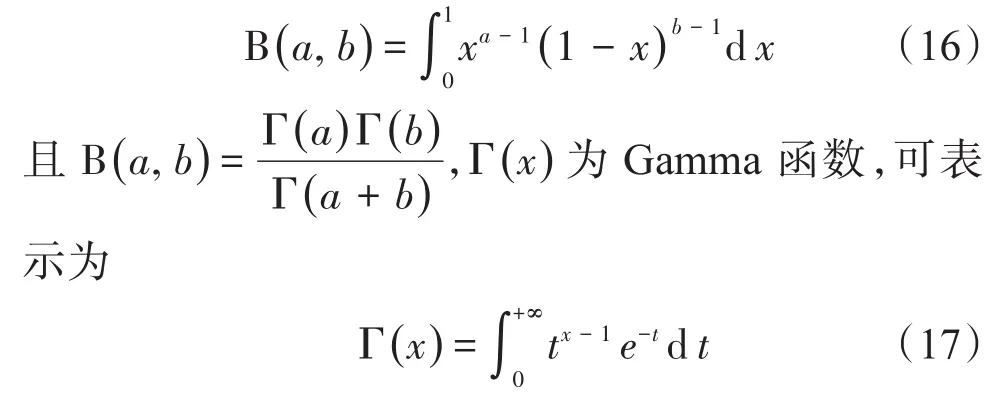
式（15）可表示为

此时最大嵌入时间tmax与有效接触应力无关，对于非线性模型（n＞1），嵌入时间依赖于有效接触应力，如式（18）所示。

2 模型验证

由于通道压裂支撑剂嵌入数据鲜有文献报道，可用的实验数据较少，为验证模型的准确性，参照郭建春等［18］和 Zhang 等［23］的经验解析模型以及Alramahii等［24］的实验数据（岩石杨氏模量为6.39 GPa；岩石半径为 2.54 cm；支撑剂目数为0.42 mm/0.84 mm；黏土体积分数为48%），将上述模型与之进行对比（图4），结果显示：①郭建春等和Zhang等的模型在低闭合压力区间拟合结果较差，而在高闭合压力阶段郭建春等的模型预测曲线有上翘延伸趋势，新模型在各压力区间均能取得较好的拟合结果；②郭建春等的模型是以闭合压力为变量的3次多项式，需确定4个无因次参数，拟合难度较大，应用受限，不利于嵌入预测；Zhang等的模型的本质为线弹性模型，是在郭建春等模型的基础上发展得到的［21］，拟合时考虑为y=a x+b的形式，形式较为简单，拟合精度在高闭合压力阶段易取得较好的效果，而新模型仅需2个参数变量，就能取得较好的拟合结果，参数拟合结果为：k=12.98 GN·m-2.3524，n=2.352 4，R2=0.990 1。

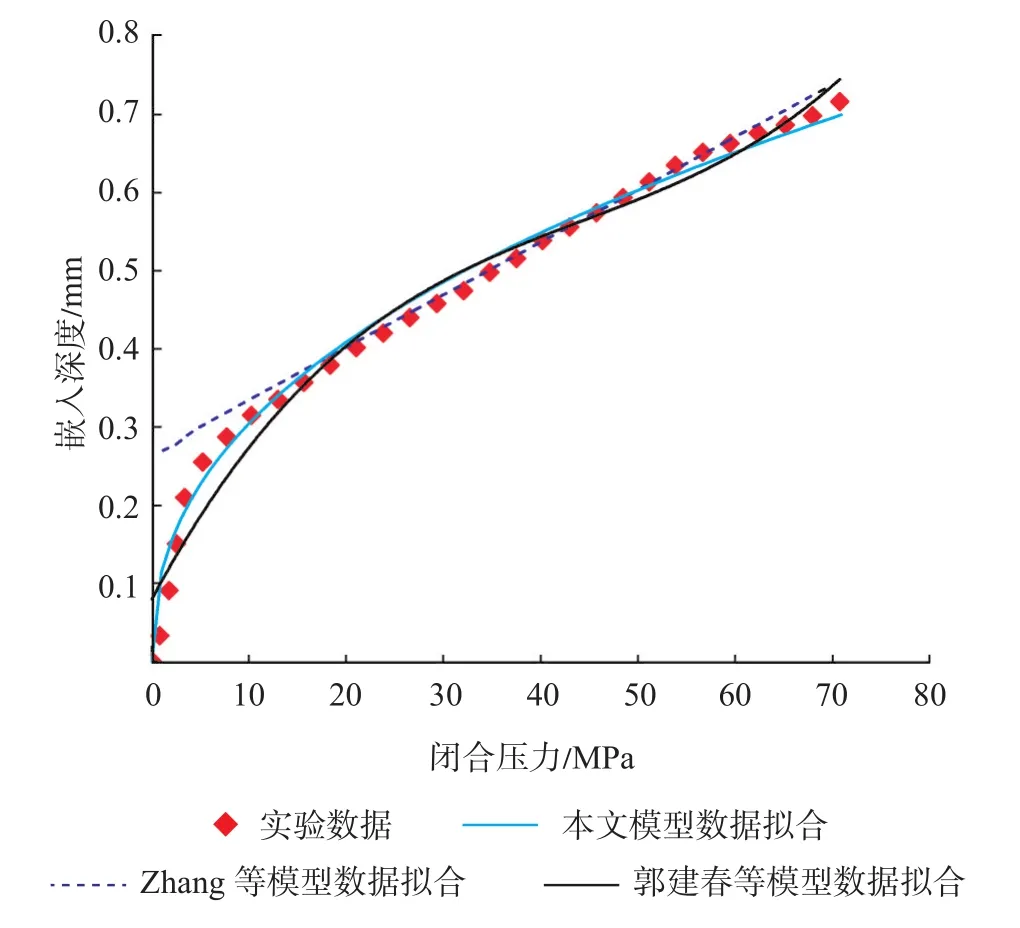
图4 模型结果对比Fig.4 Comparison of model results

3 参数分析

根据上述嵌入深度计算方法，为进一步分析参数变化对嵌入深度的影响，分别对倔强系数k、弹性指数n，以及有效接触应力σc进行了系统的分析。所取的基本参数为支撑剂支柱半径r=1.27 cm，支撑剂铺置面积比c=0.5，支撑剂支柱质量m=32 g，裂缝闭合压力σ=40 MPa，裂缝内流体压力pwf=10 MPa，支撑剂密度ρ=2.5 g/cm3；支撑剂支柱高度h=1 cm。

3.1 弹性指数影响

考虑弹性指数n对嵌入深度的影响，倔强系数在计算过程中取k=3 GN·m-n，由图5所示，在倔强系数一定的条件下，n值小幅度变化，对嵌入深度影响较大。n由1.3增加到1.6时，80 MPa下的最大嵌入深度增加了4.79倍，n值越大，储层越软，嵌入越容易，随着n值的增大，一方面增加了支撑剂的嵌入深度，另一方面增加了支撑剂非线性嵌入的压力区间。

图5 弹性指数对嵌入深度的影响Fig.5 Influence of elastic index on embedment depth

3.2 倔强系数影响

考虑倔强系数k对嵌入深度的影响，在计算过程中取n=1.6，如图6所示，当n值一定时，k的增加并不会改变非线性嵌入的压力区间，当k由5 GN·m-1.6下降到 2 GN·m-1.6时，80 MPa下的最大嵌入深度增加了1.77倍，表明k对嵌入深度的影响小于n，但对于储层岩性的标准要求二者共同作用，因此，在应用过程中，要协调二者的作用关系。

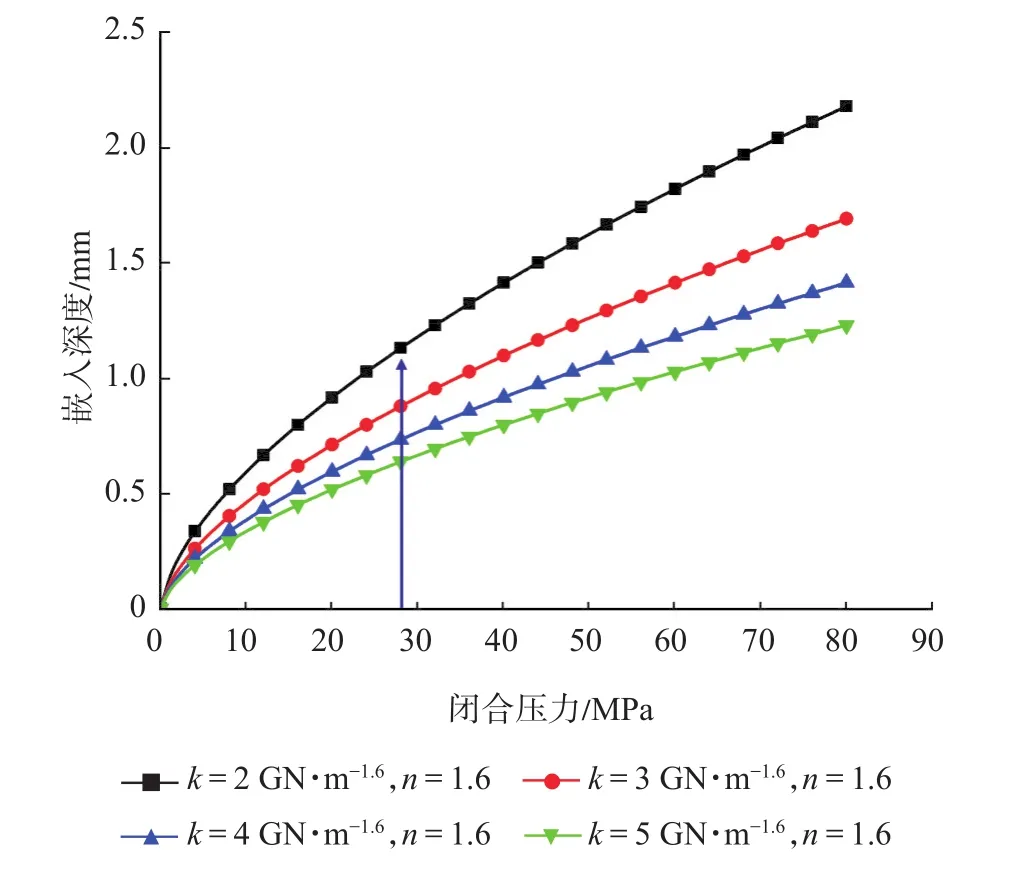
图6 倔强系数对嵌入深度的影响Fig.6 Influence of coefficient of stiffness on embedment depth

3.3 支撑剂铺置面积比影响

由式（3）可知，有效接触应力σc主要取决于裂缝内流体压力pwf及支撑剂铺置面积比c，通道压裂为等时脉冲压裂，因此c=0.5，但在理论研究中，c变化对有效接触应力有直接的影响，其大小对于嵌入深度的影响也是不容忽视的。

在不同支撑剂铺置面积比c条件下，分别计算嵌入深度计算结果，由图7所示，随着c值由0.25增加到0.75时，嵌入深度降低，80 MPa下的最大嵌入深度分别降低为c=0.25时的64.8%及50.3%。虽然提高c值可以降低支撑剂嵌入深度，但是对于通道压裂而言，高铺置面积比会减少油气流动空间，降低裂缝导流能力［26］。因此在实际应用过程中，有必要对铺置面积进行优化，以保证最大的经济效益。

图7 支撑剂铺置面积比对嵌入深度的影响Fig.7 Influence of proppant displacement ratio on embedment depth

3.4 缝内流体压力影响

支撑剂嵌入是闭合压力与流体压力综合作用的结果，当流体压力与闭合压力相等时，有效接触应力大小为0 MPa，支撑剂支柱不受嵌入的影响。如图8所示，在闭合压力为80 MPa的条件下，随着流体压力的不断降低，支撑剂受到的有效应力不断增加，支撑剂支柱的嵌入深度也不断增加；流体压力在10 MPa时，支撑剂最大嵌入深度为1.558 mm，流体压力在40 MPa时，支撑剂最大嵌入深度为1.098 mm，均远大于常规压裂方式下的嵌入深度［30-31］。显然，较小的流体压力会加大支撑剂的嵌入深度，而在相同流体压力下，增加闭合压力同样会增大有效接触应力，从而增加支撑剂的嵌入深度。

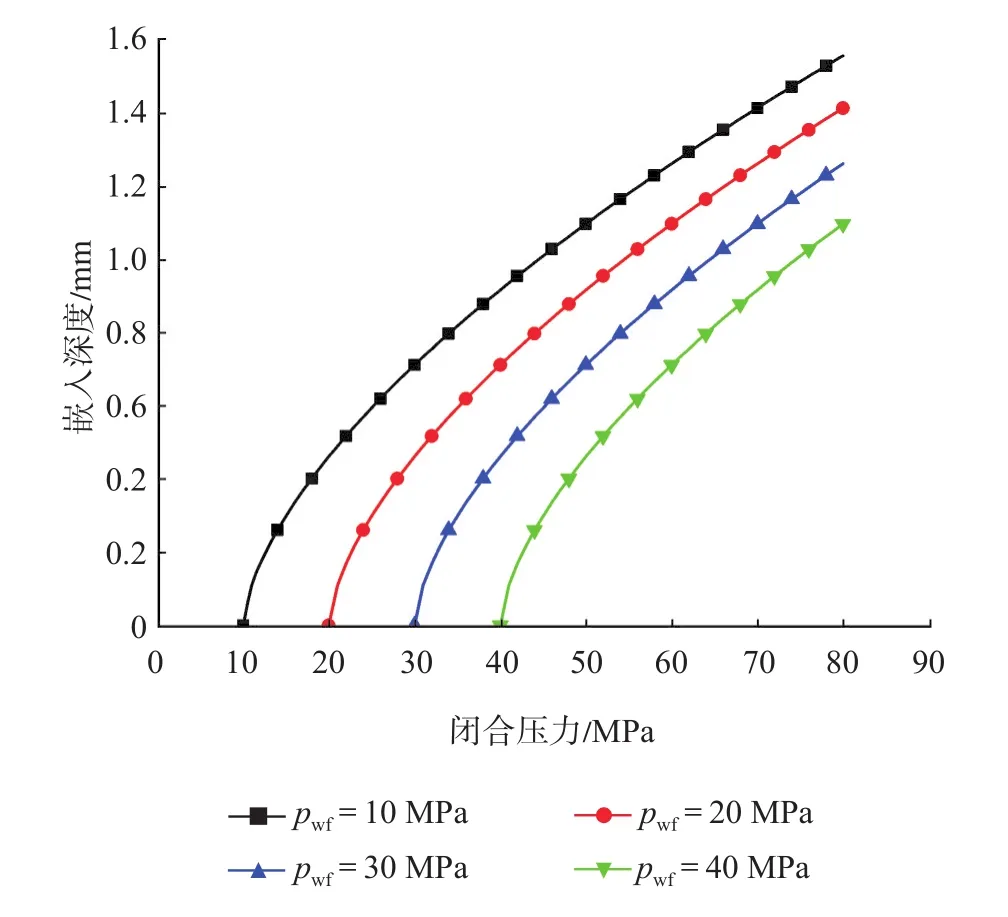
图8 流体压力对嵌入深度的影响Fig.8 Influence of fluid pressure on embedment depth

4 实验分析

在基于理论分析的基础上，为进一步了解和掌握通道压裂嵌入特征，选择了不同岩石物性岩心进行了通道压裂嵌入实验，并针对实验结果，应用本文提出的模型，进行了拟合预测，取得了较好的效果，不同杨氏模量下的嵌入数据均获得了较好的拟合效果（图9）。

随着杨氏模量的增加，支撑剂的嵌入深度随之降低。在80 MPa的闭合压力下，当杨氏模量从31 GPa增加到59 GPa时，嵌入深度从1.76 mm降为1.06 mm，杨氏模量越高，意味对应的储层硬度越大，岩石嵌入难度越大。

倔强系数与杨氏模量之间也存在着较好的对应关系（图10），在模型应用时，准确确定储层的岩石物性，是精确描述通道压裂支撑剂嵌入深度的关键。因此后期在大量实验的基础上可通过拟合经验公式得到杨氏模量与倔强系数的幂率关系。

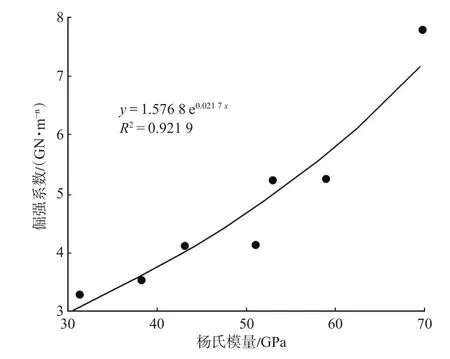
图10 倔强系数与杨氏模量拟合关系Fig.10 Relationship between coefficient of stiffness and Young's modulus

以通道压裂支撑剂支柱为研究对象，建立的支撑剂嵌入深度计算幂率模型，较Zhang等的模型和郭建春等的模型更加适用于通道压裂支撑剂嵌入的理论分析和计算，同时，由模型计算得到的支撑剂嵌入深度可进一步引入到导流能力的计算中，进而分析导流能力变化，优化压裂设计。尽管本模型对通道压裂嵌入过程的描述较其他模型有明显的优势，但仍存在不足之处：①对支撑剂的嵌入分析为弹性嵌入、弹塑性嵌入以及塑性嵌入综合计算结果，无法区分三者之间的计算界限，无法准确计算弹性嵌入、弹塑性嵌入以及塑性嵌入各阶段的嵌入深度；②在计算过程中假定支撑剂铺置面积比c为一定值，而实际过程中，支撑剂支柱面积在低闭合压力阶段是动态变化的，因此在计算过程中会对倔强系数k和弹性指数n产生拟合误差；③本模型还忽略了支撑剂破碎以及微粒运移带来的计算误差，进一步研究需考虑支撑剂铺置面积比以及支撑剂破碎等问题影响。