基于超二次曲面模型的超声阵列成像算法*
2019-09-11李西红
季 宁, 杨 涛, 李西红
(1.西南科技大学 信息工程学院,四川 绵阳 621010;2.西南科技大学 特殊环境机器人技术四川省重点实验室,四川 绵阳 621010)
0 引 言
随着机器人技术的发展,机器视觉的研究受到研究者的日益关注,目标物体的三维成像对机器人独立完成任务起关键作用。目前常用于成像的传感器有相机、深度传感器和激光扫描仪等,但是其在核辐射、强粉尘、黑暗、烟雾等特殊环境中发挥作用有限。雷达与声呐虽可在这些环境中工作,但雷达成本较高,声呐存在波束分辨率低、扫描速度慢等固有缺陷。因此基于超声阵列的三维目标成像具有重大研究价值。目前超声成像技术主要用于医学成像与无损检测方面[1],空气中的超声三维成像研究较少。
文献[2]利用采集到的回波数据和图像几何的先验知识来估计和校正成像参数误差,生成自动聚焦图像,但该方法得到的图像模糊,难以分辨出目标物。文献[3]为了提高最小方差超声成像算法的分辨率、对比度以及对噪声的鲁棒性, 提出了一种改进的最小方差成像算法,实现了点目标物的成像,但未对目标物的三维成像进行进一步研究。文献[4~6]利用被检测目标物的方向角来实现超声阵列对目标物的检测与识别,本文在此基础上,利用渡越时间法(time of flight,ToF)得到特征点与超声阵列之间的距离信息,从而得到目标物特征点的坐标信息,对三维数据点进行超二次曲面拟合以实现目标物的三维成像[5,6]。
文献[7]提出了基于遗传算法的两阶段拟合方法,实现了超二次曲面三维模型的重构,但遗传算法需要调整较多的参数,计算效率较低。文献[8]通过激光扫描仪获得散乱点云数据,根据点云中目标表面各点到目标的均方距离,建立了三维目标位姿估计的非线性目标函数,实现了三维目标的定位。文献[9]将超二次曲面参数拟合问题转化成非线性最小二乘问题,用Levenberg-Marquardt 算法进行参数拟合,但LM算法不适用于目标函数非线性程度很高的大残量问题。
综上所述,本文通过超声阵列围绕目标物旋转,分别从目标物的前、后、左、右、上、下六个方向获得回波信号,对回波信号峰峰值时间进行切分,采用改进的Unitary-ESPRIT算法对每个时间片段回波信号中特征点的方位角进行估计,同时根据渡越时间法得到特征点与发射阵列之间的距离,利用三角几何关系计算特征点的坐标,对其进行坐标变换以得到特征点在全局坐标系下的坐标。借助改进的LM算法对目标物的特征点数据进行参数拟合,获得超二次曲面参数,以实现目标物的三维成像。
1 超声阵列的分布
超声波换能器的中心频率会直接影响超声波的衰减系数和吸收系数,进而对空间中超声波的声场分布产生影响,提高超声波换能器的中心频率可提高横向分辨率,但是超声波频率过高会造成数据量大和衰减过大,不利于信号的采集和处理。为了在保证检测精度的同时避免超声波能量的过快衰减,本文选择频率为40 kHz的波换能器。随着超声波换能器直径的增大检测的空间分辨率会提高,同时引起栅瓣的几率也会增大。在综合考虑了分辨率及栅瓣等因素后,选择压电片直径为11 mm的超声波换能器。
对制作成本、衰减、分辨率等因素进行综合考虑后[10],本文接收阵列采用阵元间距为25 mm 、阵元大小为8×8的二维面阵,发射阵元采用单发射方式且位于接收阵列中间。超声阵列排布如图1所示。

图1 超声阵列排布示意
2 空间特征点坐标信息的获取
通过渡越时间法与改进的Unitary-ESPRIT算法[11]得到空间特征点与超声阵列之间的距离及其对应的方位角,并将其转换为坐标,关系如图2所示。

图2 空间特征点投影示意
由图2可获得每个空间特征点的坐标,xk=dtanθcosφ,yk=dtanθsinφ,zk=d。其中,θ为z轴与OP的夹角,φ为OP在xoy平面的投影与x轴的夹角,d为特征点与发射阵列之间的距离。
本实验从目标物的前、后、左、右、上、下六个方向来获得特征点的坐标,利用坐标变换对空间特征点以阵列中心为原点的局部坐标系下的坐标进行转换得到以物体中心为原点的全局坐标系下的坐标,从而获得目标物全部特征点在全局坐标系下的坐标。
2.1 特征点距离信息的获取
利用TOF来计算特征点的空间距离的基本原理为:从发射阵列发射的超声波在反射点处所形成反射回波中提取特征点,再根据发射与接收的时间差来计算特征点的空间距离。
所有特征点都包含在渡越时间为的回波信号中。将时间段Δt等分为多个时间段,求出这些时间片段所对应的空间特征点,并用Unitary-ESPRIT算法得到相应的仰角和方位角,当时间片段很小时,可以认为这段时间内所对应波形的所有特征点都在与发射阵列距离相等的等距面上。由于不同特征点所对应的方位角和仰角不同则分布在等距面上的位置不同,其与发射阵列的距离可以利用这一小段时间的中心值与阵列发射信号速度的关系函数来确定。
2.2 空间特征点的波达方向估计
波达方向(direction of arrival,DOA)估计算法中MUSIC算法需耗时较长,Capon算法空间分辨率较低;ESPRIT算法虽然有耗时小、分辨率高的优点,但其对相干源的分辨率还是较低。为解决相干源问题,将空间平滑去相干算法和Unitary-ESPRIT算法相结合。该算法基本过程如下:
1)利用去相干平滑算法获得输出信号矩阵X对应的协方差矩阵Rxx。
2)计算出实矩阵对应的协方差矩阵Ryy
Ryy=(QN⊗QM)Rxx(QN⊗QM)H
(1)
式中 ⊗为Kronecter积,M,N分别为x,y方向阵元数量。当M或N为奇数时,QN与QM的表达式
(2)
当M或N为偶数时,QN与QM的表达式

(3)
3)根据[Re(Ryy),Im(Ryy)]对相关矩阵进行估计。
4)对相关矩阵进行特征值分解后取较大的特征值的信号矢量,从而构成平滑后的信号子空间Es。
5)通过特征分解获得特征值,从而估计出信源方向角。
3 二次曲面参数拟合
二次曲面是由三元二次方程所表示的曲面,因其具有局部变化不敏感和视点不变性等优点而被广泛应用于计算机图形学、计算机视觉等领域。其标准方程为[12]
(4)
式中 (x,y,z)为超二次曲面上的点,a1,a2和a3为超二次曲面在x,y,z方向的尺寸参数,ε1和ε2为形状参数。当参数ε1和ε2发生改变时可以形成不同的曲面。对式(4)进行变形可扩大超二次曲面模型的表示范围。超二次曲面的变形公式
(8)
式中μx,μy为由锥化参数kx,ky定义的锥化函数。
对空间三维点数据进行超二次曲面参数拟合时需计算空间三维点与超二次曲面之间的距离
(9)
设超二次曲面中心为O,其与空间三维点P的连线为OP。则式(9)中d0表示OP的长度,ds表示OP与超二次曲面上的交点到点O的距离。为了实现全局误差最小,可将其转化为非线性最小二乘优化问题,则拟合误差f为
(10)

目前常用的超二次曲面参数拟合方法中牛顿法很难收敛即使收敛找到点也未必最优,最速下降法存在锯齿现象且计算效率较低。此外,考虑到本实验特征点数量较多,用遗传算法寻找最优解耗时较长。LM算法[13]比共扼梯度法和梯度下降法收敛速度更快,但该算法拟合效果受初值影响较大,因此,本研究利用改进的LM算法[14]对超二次曲面参数进行拟合。其迭代规则如下
xi+1=xi+h
(11)
式中xi为参数向量,h为迭代步长
(12)
式中λ为比例因子。目标函数实际减小量和估计减小量之比r为
(13)
算法的实现过程如下:
1)设置x0,λ的初值与最小值λmin。
2)计算雅克比矩阵J,更新目标向量。
3)计算在xi+1处目标函数f的值。
4)计算目标函数的值并根据式(13)对r值进行判断。当r值大于0时接受该参数向量,反之则放弃。当r值接近0时,使λ増大4倍;当r值接近1时,则λ如式(12);当r值在0与1之间时,λ值不变。返回步骤(2)获得新的xi+1,直至f的值满足要求。
4 仿真结果分析
采用MATLAB软件工具,模拟8×8的超声阵列作为阵列模型,为了获得目标物整体的特征点信息,对几何物体超声阵列分别从物体前、后、左、右、上、下六个方向进行超声波发射与接收仿真,在每个方向上利用Unitary-ESPRIT算法获取对应的特征点方位角信,同时根据渡越时间法得到该方向上空间特征点的距离。将角度与距离转换为以阵列中心为原点的特征点坐标。进行适当的坐标变换得到该方向上的特征点在以物体中心为原点的坐标系下的坐标信息。最后将从六个方向得到的特征点坐标信息进行汇总,得到物体的全部特征点信息,拟合出该物体对应的超二次曲面参数,从而得到几何物体的三维图像。
实验过程中考虑到阵列的接收范围与可识别角度,超声阵列与目标物的距离设置为1 m。本问题属于大残量问题, 初值取0.6。
图3(a1),(b1),(c1)为超声阵列获得的球体、长方体、圆柱体特征点坐标信息,图3(a2)(b2),(c2)为LM算法拟合后得到的物体图像,图3(a3),(b3),(c3)为LM改进算法拟合后得到的物体图像。
利用LM算法与LM改进算法对球体特征点进行拟合得到的参数实验数据分别如表1所示。

表1 球体参数LM算法改进前后拟合实验数据
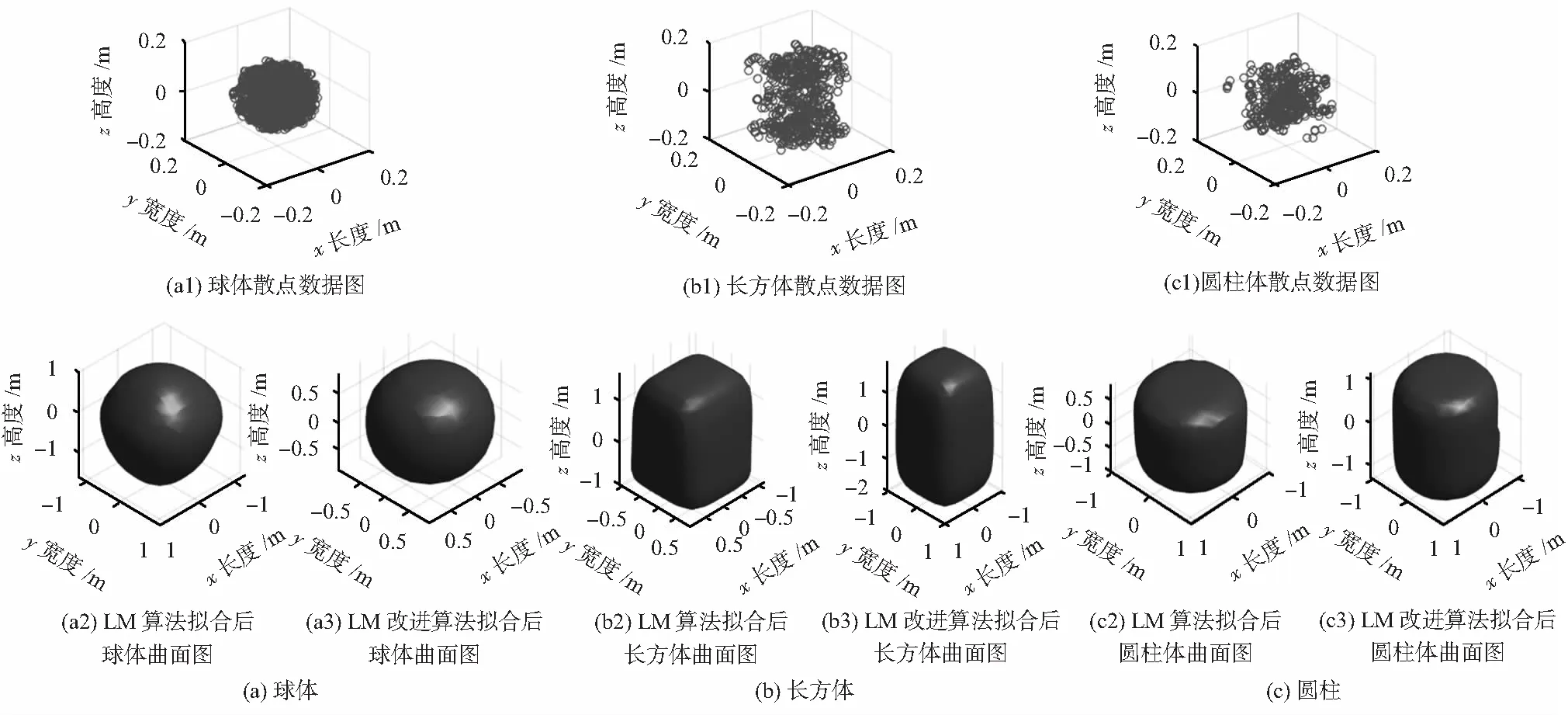
图3 三种形状体数据拟合前后对比
利用LM算法与LM改进算法对长方体特征点进行拟合得到的参数实验数据分别如表2所示。

表2 长方体参数LM算法改进前后拟合实验数据
利用LM算法与LM改进算法对圆柱体特征点进行拟合得到的参数实验数据分别如表3所示。

表3 圆柱体参数LM算法前后改进拟合实验数据
在实验过程中随机选取了多组初值进行拟合,LM算法拟合时初始值的选取对结果影响较大,拟合到的参数未必能得到目标物的图片,初始值选取不恰当时则无法拟合出超二次曲面参数,利用改进的LM算法拟合则较好地改善了这一问题,拟合结果优于LM算法。表1、表2、表3是选取其中一组初值得到的拟合参数,从表中可看出两种得到的拟出合参数值与标准参数值之间存在一定误差,但改进的LM算法的参数误差普遍小于LM算法的参数误差,且改进后LM算法的参数误差基本控制在10 %以内。图3给出了两种算法拟合后球体、长方体以及圆柱体的图像,从中也可看出LM改进算法拟合后的图像效果更好。
5 结 论
本文通过超声阵列获得物体的回波信号,并对其峰峰值时间进行切分,利用Unitary-ESPRIT算法与渡越时间法得到空间特征点坐标信息,通过改进的LM算法拟合出超二次曲面参数,最终实现三维目标的成像。由仿真结果可知:该算法可有效解决LM算法对初值依赖过大的问题。本方法可扩展到多目标对象的复杂场景三维成像,也可对方向角估计算法进行改进,以达到更好的效果。
