基于排气温度动态模型的在线观测器研究

李佳蔚， 崔涛， 刘宇航， 师帅楠， 孙强

(1.北京理工大学 机械与车辆学院， 北京 100081； 2.北京航天发射技术研究所， 北京 100076; 3.河北华北柴油机有限责任公司， 河北 石家庄 050081)

0 引言

发动机是汽车的心脏，柴油发动机更具有燃油效率高、动力性能强和稳定可靠等特点，近年来在发电、汽车、船舶交通、采矿等行业得到广泛应用并发挥了至关重要的作用[1-2]。柴油机稳定运行是其在生产生活中应用的重要前提，因此受到越来越多的关注。

热力性能参数的监视和趋势预测是发动机状态监测的主要内容，发动机排气温度可以间接反映缸内燃烧状态,是实际监测中最常用的气动热力性能参数[3-6]。当柴油机缸内燃烧恶化时，排气温度会显著升高，不仅造成油耗增高、功率降低，还会增大零件的热疲劳、降低柴油机的使用寿命[7-8]。通过监视和预测排气温度，能够掌握柴油发动机的运行状况。

柴油机在运行过程中，排气温度是一个随时间不断变化的参数，无法用确定的数学模型来表征。传统方法基于热平衡方程和能量守恒，包括：顾宏中提出的排气温度计算模型[9]；由热力学第一定律能量流入流出推导排气温度的计算式[10]；从热平衡方程角度介绍的排气温度计算方法，即热力学第一定律的修正模型[11]。不同于传统建模方法，藏军[12]、姜兴家[13]采用时间序列方法对柴油机状态参数进行趋势预测研究；丁刚等[14]利用神经元网络方法对航空发动机排气温度进行预测；于广滨等[15]从泛函分析的角度，建立基于支持过程向量机的时间序列预测模型；王新全等[16]建立了基于反向传播(BP)神经网络的时间序列预测模型，并用遗传算法(GA)对模型的权值和阈值进行优化；杨洪富等[17]采用长短时记忆(LSTM)网络构建航空发动机排气温度预测模型，提出了基于LSTM的航空发动机排气温度预测方法；雷伟[18]通过合理算法对由传感器测量的排气温度数据进行融合，得到了较准确的测量值；张红涛等[19]通过建立数学模型，计算得到非标准大气的修正系数和调节规律的修正系数，提出了考虑非标准大气和调节规律使用因素的涡扇发动机排气温度换算方法。

上述研究工作中均没有考虑模型的动态响应性能，为了达到良好的计算精度和动态响应性能的要求，本文以某型号柴油发动机性能仿真模型为研究对象，基于能量守恒，采用模型和统计相结合的方法，建立排气温度观测器模型，以期为后续的故障诊断策略和容错分析算法的研究提供基础。

1 涡后排气温度模型

1.1 涡前温度均值模型

将气缸模块视为开口系统，通过热力学第一定律对进出系统的能量进行分析，从而得到排气温度表达式[10]如下：

(1)

(2)

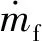
(3)

1.2 涡后温度均值模型

排气温度观测器的用途是对排气温度传感器进行在线故障诊断，排气温度是指2级涡轮增压系统低压级涡轮出口的气体温度(见图1)，因此需要建立涡后温度均值模型。

图1 2级涡轮增压系统图Fig.1 Two-stage turbocharging system

涡轮机与压气机通过连接轴实现功率关联。忽略传热，假定流经涡轮的废气为理想气体，涡轮机输出功率Pt可以表示为

(4)

式中：cpgx为废气等压比热容；Te为排气温度。

同理，压气机的消耗功率Pk可表示为

(5)

式中：cpk为进气等压比热容；Tc为压气机出口温度；Ta为环境温度。

在忽略传热情况下，假定流经涡轮的废气为理想气体，由涡轮机与压气机之间的功率平衡，得

Pt=Pk.

(6)

联立(4)式、(5)式和(6)式，得

(7)

流入气缸空气的能量变化由压气机吸收能量和中冷器散失能量共同组成，定义空气在压气机中的温度变化占空气流入过程中总温度变化的比例为η，则有η=(Tc-Ta)/(Ti-Ta)，(7)式可进一步化为

(8)

(8)式构成了完整的柴油机排气温度均值模型，模型输入量是空燃比、涡前温度因子、环境温度和进气温度，涡后排气温度则是模型输出量。

本文排气温度观测器要求为具有良好的计算精度和动态响应性能，因此需要对均值模型进行优化。

2 模型优化

2.1 温度比例因子优化

将(8)式中η和比热容的比值视为1个与中冷器效率、压气机效率相关的系数—比例因子k，k=η(cpk/cpgx)，通过公式拟合后代入(2)式，(8)式可化简为

(9)

式中：ΔTT为涡轮前后温度差；ΔTK为进气过程中空气温度差。

通过多组仿真数据对2级增压高压级出口温度Tc和进气温度Ti进行仿真，二者取值分别在343～453 K和313～353 K，环境温度Ta为298 K,cpk/cpgx在0.95～1.00之间[20]，比例因子k在2.68～3.00范围内波动，因进气前后温度差值小于55 K，即比例因子k的取值误差对排气温度的影响不会超过10 K，故可将其视作常量，本文中选取中间值2.84，排气温度稳态模型的数学表达式如下：

(10)

2.2 排气温度因子优化

通过排气温度影响参数的分析可知，除了作为输入参数的环境温度、进气温度、燃油质量流量和空气质量流量外，还需要确定排气温度因子Kt值，才能使得排气温度稳态模型得以实现。由排气温度因子Kt表达式可知，Kt值主要受燃油流量和发动机转速的影响。

以某型号发动机为研究对象建立性能仿真模型[21]，使用发动机工作过程模拟计算软件GT-POWER构建性能仿真模型(见图2)，讨论影响排气温度因子Kt的参量，通过优化Kt，得到涡后排气温度Te的求解方法。

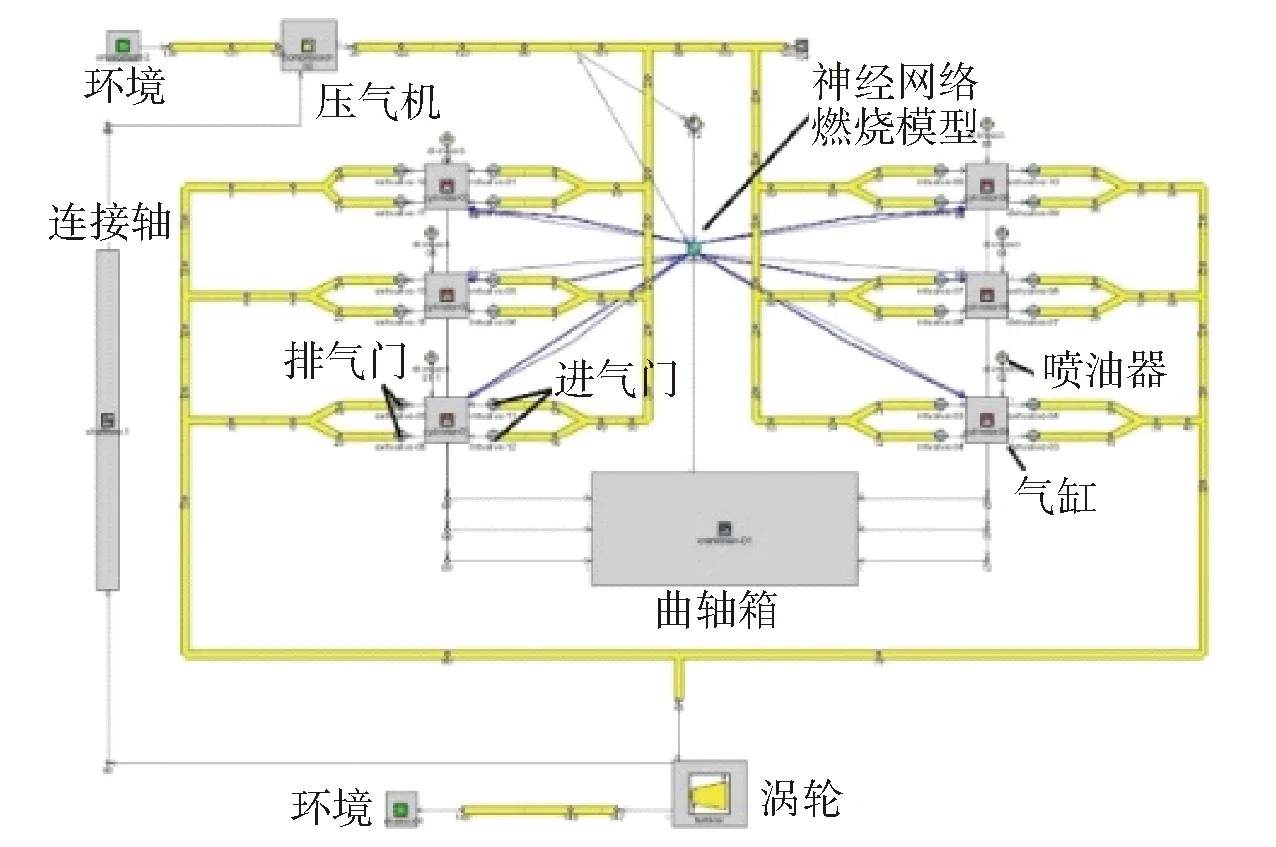
图2 柴油机性能仿真模型Fig.2 Simulation model of diesel engine

2.2.1 循环喷油量影响

发动机转速为2 100 r/min、循环喷油量为79.7～199.7 mg的仿真结果如图3所示。由图3可见，在空燃比大于40时，缸内平均指示压力上升，排气能量增加，涡轮机获得的能量增加，涡轮转速提高，压气机压比增大，使得空气流量增加。受压气机流量特性影响，压气机压比增加的幅度无法跟随循环喷油量的增加幅度，空气流量增加有限。空气流量的相对不足使得空燃比降低，单位质量的工质获得更多的能量，导致排气温度升高。

图3 发动机在2 100 r/min下循环喷油量对排气温度的影响Fig.3 Effect of cycle fuel injection on exhaust gas temperature at 2 100 r/min

2.2.2 喷油提前角影响

喷油提前角的大小决定着整个燃烧相位分布。随着喷油提前角的增大，滞燃期内的可燃混合气增多、滞燃期变长，从而导致燃烧始点提前，燃烧速率增加，缸内最高燃烧温度和最大爆发压力升高，排气温度降低。

设计如表1所示的仿真工况，选取2 100 r/min外特性工况参数，在不同喷油提前角条件下进行仿真，研究喷油提前角(绝对值)对涡后温度的影响规律。如图4所示，随着喷油提前角的增大，燃烧50%累积放热量时的曲轴转角提前、燃烧重心前移，指示热效率升高，导致废气能量所占比重下降。如图5所示，排气温度随着提前角增大，呈下降趋势。在功率损失较小范围内，喷油提前角每增加1 °CA，涡后排气温度下降约4 K.

表1 喷油提前角影响规律仿真工况

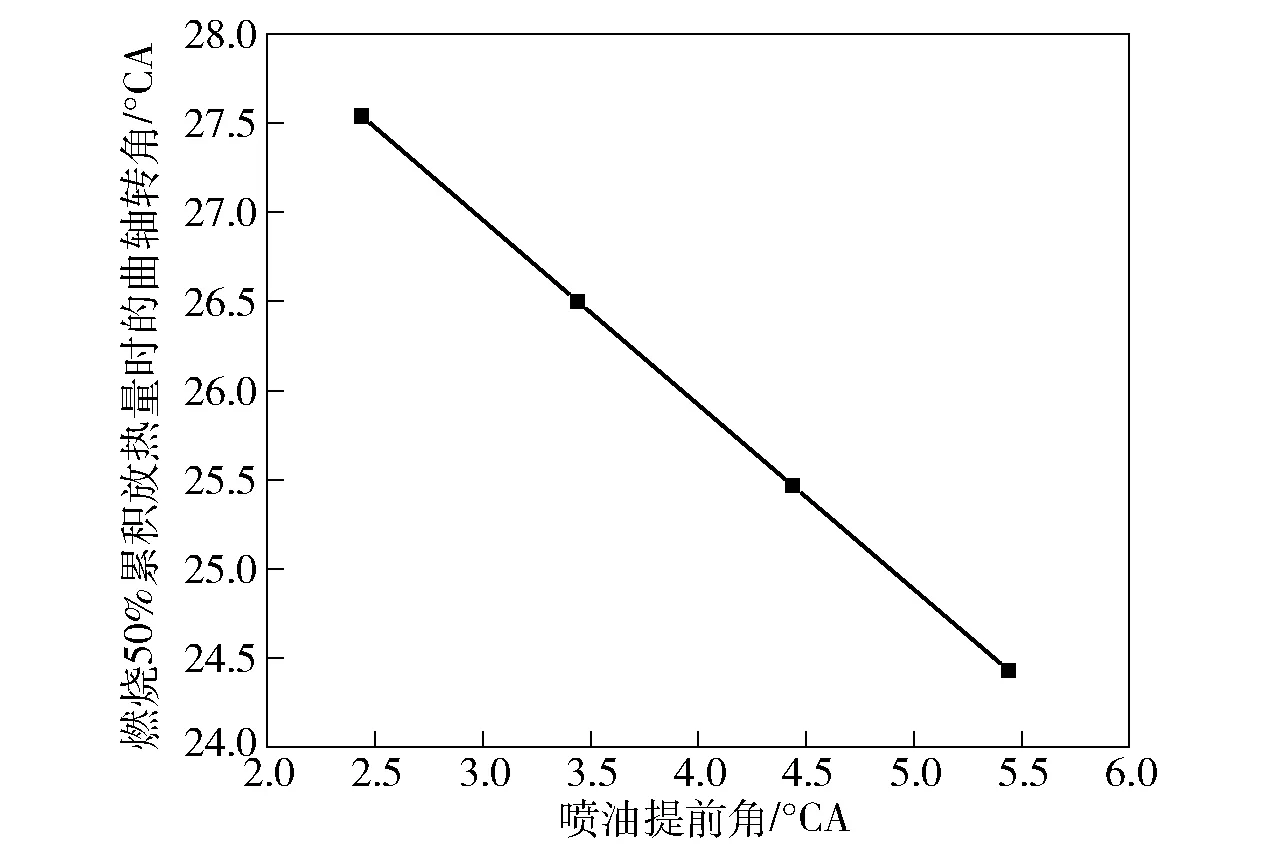
图4 喷油提前角对燃烧过程的影响Fig.4 Effect of fuel injection advance angle on combustion in cylinder

图5 喷油提前角对排气温度的影响Fig.5 Effect of fuel injection advance angle on exhaust gas temperature

实际试验中重载车辆负荷为60%时，排气温度为700 K左右，喷油提前角改变1°CA，相对误差在0.6%左右。本文中搭建的排气温度观测器用于对排气温度传感器的在线故障诊断，为满足在线计算的能力，在相对误差较小情况下，不单独考虑。

2.2.3 转速影响

设计循环喷油量为200 mg，海拔高度为0 m，转速分别为1 300 r/min、1 500 r/min、1 700 r/min、1 900 r/min以及2 100 r/min的仿真工况，在不同转速条件下进行仿真，研究转速对柴油机排气温度的影响规律。仿真结果如图6所示。由图6可见：排气温度随转速的上升，呈先下降、后上升趋势；低转速时，增压器进气不足，燃烧恶化，排气温度较高；中间转速时，增压器工作性能良好，空燃比增加，指示热效率增加，排气温度较低；高转速时，空燃烧时间变短，气量增加不明显，排气温度增加。

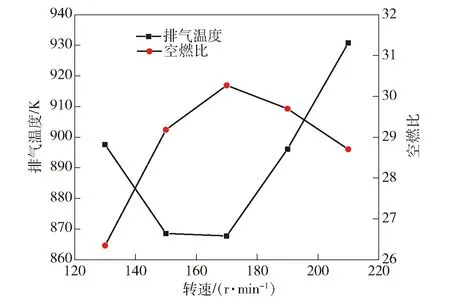
图6 发动机转速对排气温度的影响Fig.6 Effect of engine speed on exhaust gas temperature

通过上述对排气温度影响参数规律的分析可知，通过(3)式计算的柴油机排气温度因子Kt主要与空燃比和柴油机转速相关。设计如表2所示的仿真工况，在平原环境下进行不同转速、不同负荷的仿真，通过仿真数据结果进行参数拟合，进而求得排气温度因子Kt的查表图，结果如图7所示。

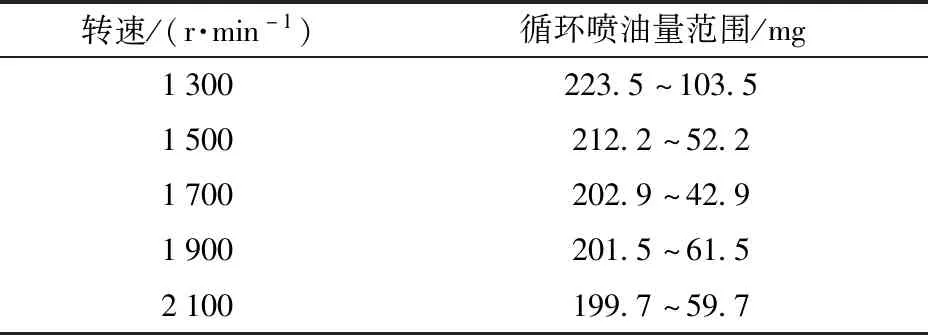
表2 Kt影响因素(转速、空燃比)仿真工况

由图7可见，在空燃比不变条件下，排气温度因子随转速的提高呈增大趋势。在转速不变前提下，排气温度因子随空燃比的增大呈减小趋势。

图7 海拔0 m时Kt的查表图Fig.7 Kt at an altitude of 0 m

2.2.4 海拔修正系数

排气温度因子Kt在不同转速以及不同海拔高度工况下并不是1个常量。在表2的仿真工况基础上，对不同的高原环境进行仿真。

由于不同海拔下的涡前温度因子仿真结果与0 m仿真结果具有比例近似性，不同高度海拔下涡前温度因子查表图可根据平原环境下涡前温度因子查表图乘以海拔修正系数求得，在海拔2 000 m和4 500 m时的结果如图8和图9所示。经计算验证线性误差在3%以内。

图8 海拔2 000 m时Kt的查表图Fig.8 Kt at an altitude of 2 000 m

图9 海拔4 500 m时Kt的查表图Fig.9 Kt factor at an altitude of 4 500 m

由上述分析可知，缸内燃烧是排气温度的主要影响因素，通过分析空燃比、转速和海拔对排气温度因子Kt的影响，即可得到燃烧对Kt的影响，其仿真结果如图7～图9所示。由图7和图8可见，表征中冷器冷却效率和压气机效率对排气温度影响的比例因子k取2.84时，中冷器效率差异对排气温度带来的影响不会超过10 K. 因此给出在Simulink下搭建的考虑多因素影响的排气温度优化模型如图10所示。

图10 排气温度稳态模型Fig.10 Steady state model of exhaust temperature

3 观测器构建

3.1 观测器动态修正

除了第2节分析的排气温度影响因素，外排气温度动态计算还受排气与传感器外壳的换热过程、传感器信号相对发动机燃烧存在滞后、增压器惯量、排气管容积效应等影响。由于过程环节较多，为满足在线计算需要，本文通过模型分析和数据拟合的方法将滞后效果加入稳态模型中，构建排气温度动态模型，从而满足实车工况下对排气温度进行动态预测的要求。

在各环节中以排气与传感器外壳的换热过程作为主要考虑因素，建立对流换热方程。假设热交换中没有热损失，则其工作端的热平衡方程为

(11)

(12)

式中：α为对流传热系数；F为热接点表面积；T为介质真实温度；Tj为热接点温度；c为热接点比热；ρ为热接点材料的质量密度；V为热接点体积。

(11)式为牛顿冷却定律，该定律表明向感温元件传热的速度正比于周围介质与元件间的温度差。以τ为热电偶的动态指标，称为时间常数，τ=αF/(cρV)代入(11)式，得

(13)

3.2 1阶滞后环节参数设计

考虑传感器对流换热方程为1阶传递函数形式，故采用1阶滞后环节替代，即在原有模型后串联1阶滞后环节，模拟排气温度因惯性引起的滞后趋势。由于排气温度观测器输出信号为离散信号，使用数字式1阶滞后环节进行修正。

数字式1阶滞后环节的一般表达形式为

(14)

式中：zp为补偿器的极点值；Kd为增益，Kd=1-zp，Kd的作用为消除稳态误差，即z=1时保证G(z)=1.

将z变换传递函数形式转化为可以应用于控制系统中的离散时间传递函数，使校正补偿器具有应用意义。设输入函数为E(z)、输出函数为U(z)，则(13)式可化为

U(z)=zpz-1U(z)+KdE(z)，

(15)

z变换的定义为

(16)

故(14)式可化为

u(k)=zpu(k-1)+Kde(k).

(17)

由(17)式可知，数字式1阶滞后环节的输入不仅与该时刻的输入相关，还与上一时刻的输出值存在联系。数字式1阶滞后环节可以看做是一种以稳态模型的预测值作为输入信号的滤波器，极点zp越大，滤波结果越平稳，但是灵敏度越低；极点zp越小，灵敏度越高，但是滤波结果越不稳定。

对1阶滞后环节的传递函数采用z变换与拉普拉斯变换。由热电偶时间常数τ和柴油机实际运行中对排气温度的采样时间间隔，可计算出补偿器的极点值zp约为0.99. 极点zp确定后增益Kd也得以确定，理论值为0.01，但由于拟合得到的热电偶时间常数不精确与柴油机系统自身阶次的复杂性，增益Kd应根据实际情况在理论值附近小范围内进行调节，以满足模拟需求。故用于修正稳态模型的数字式1阶滞后环节的传递函数为

(18)

式中：Kd=0.011 6. 观测器结构如图11所示。

图11 排气温度在线观测器Fig.11 Exhaust gas temperature online observer

4 排气温度观测器校验

稳态情况下，软件在环采用MATLAB和GT-Power软件联合仿真的方案，对观测器输出的预测值与柴油机性能仿真模型输出的仿真值进行对比验证，即向GT-Power软件中搭建的柴油机模型输入验证工况参数，再将仿真数据结果与验证工况参数、比例因子一同输入排气温度观测器中，通过对比排气温度稳态模型输出的排气温度预测值与柴油机性能仿真模型输出的排气温度仿真值之间的误差，评价排气温度稳态模型的准确程度。由于在建立排气温度因子查表图的过程中进行了大量的标定仿真，选取标定仿真工况以外的工况作为验证工况，设计验证工况如表3所示。

表3 排气温度稳态模型的验证工况

如图12所示，将排气温度稳态模型预测值与柴油机性能模型仿真值进行对比，排气温度的预测值与仿真值差值范围在-20～20 K之间。由图13和图14可见，稳态工况下,排气温度观测器精度基本可以保持在±3%以内，表明稳态工况下观测器精度满足要求。

图12 排气温度稳态模型验证Fig.12 Verification of steady state model of exhaust gas temperature

图13 不同转速外特性条件下修正误差Fig.13 Correction errors of engine external characteristics at different speeds

图14 不同转速50%负荷条件下修正误差Fig.14 Correction errors at different speeds under 50% load condition

通过实时代码生成技术将Simulink模型实时代码生成技术移植于以MPC5554为硬件构架的柴油机控制器中，通过实车试验在线对观测器的准确性进行验证，实车测试结果如图15、图16和图17所示。

图15 大负荷时动态模型的验证结果Fig.15 Verified results of dynamic model under heavy load condition

图16 动态突变工况的验证结果Fig.16 Verified results of dynamic model under dynamic mutation condition

图17 小负荷时动态模型的验证结果Fig.17 Verified result of dynamic model under small load condition

动态测试结果表明：排气温度观测器可避免排气温度预测值的高频震荡，响应时间在3 s左右，在循环喷油量变化在100～250 mg时，误差范围保持在±20 K；整车起步过程中，循环喷油量由30 mg变化到240 mg，误差范围保持在±27 K；大负荷回至怠速时，循环喷油量由240 mg恢复至30 mg，误差范围保持在±40 K，能够很好地跟随排气温度传感器采集值的变化趋势，符合故障诊断对观测器的设计要求。

动态工况下由于转速波动、增压器工况动态变化以及进气测量的滞后影响，导致空燃比计算误差较稳态时要大，且受Kt查表精度的限制，引起排气温度观测器对实际排气温度估计的误差。

由图15可见，大负荷时空燃比较小，大部分能量被工质带走，排气管对外散热造成的误差比重相对较小，观测器估计值与实际排气温度相差20 K.

由图16可见，整车起步过程中，由怠速到2挡行驶中，排气温度上升，排气管壁温度较低，热量由排气传给管壁，排气温度缓慢上升，温度变化滞后，观测器计算精度较差，在起步时刻，观测器估计值与实际排气温度相差27 K.

由图17可见，由大负荷回至怠速后，排气温度下降，排气管壁面温度仍较高，热量由管壁传给排气，排气温度缓慢下降，温度变化滞后，同时空燃比增大，Kt误差增加，观测器计算精度较差，但是瞬态时排气温度偏差仍可以控制在±8%以内,表明瞬态排气温度观测器的观测效果是有效的。

5 结论

本文以某特定型号柴油发动机性能仿真模型为研究对象，基于能量守恒建立排气温度观测器模型，实现对排气温度的预测。通过仿真和实际实车试验，得到以下主要结论：

1)基于热力学第一定律和增压器能量平衡方程，建立反映缸内燃烧状况的排气温度动态模型。

2)涡前排气温度模型中温度比例因子的取值误差对排气温度估计值的影响不超过1.5%. 引入排气温度因子海拔修正系数，该参数取值误差对排气温度估计值的影响不超过3%.

3)考虑传感器响应性和排气管的容积效应，对观测器进行动态修正，添加1阶滞后环节。经计算确定极点值为0.99，增益为0.011 6.

4)稳态校核结果表明观测器误差在±3%以内；在实车动态条件下，观测器误差在±8%以内。观测器输出响应时间小于3 s，满足排气温度传感器在线故障诊断需要。

后续将在此基础上利用大数据收集大量工况点样本，即排气温度、排气温度观测器模型的输入(转速、循环喷油量、空燃比、环境温度、进气温度和海拔高度)对样本进行处理，使观测器适应来自环境和被诊断对象的影响。同时，通过自学习提高排气温度因子Kt的精确度，进一步提高观测器的准确性，降低对故障的误报和漏报，提高观测器容错能力。