超声局部共振系统设计与试验研究

李鹏涛, 赵波， 赵重阳， 王毅

(河南理工大学 机械与动力工程学院, 河南 焦作 454000)

0 引言

超声加工具有极强的切削能力以及极高的强化能力[1]，广泛应用于超声车削、磨削、钻削、镗削、焊接、滚压等诸多领域[2-7]。超声振动系统是超声加工的核心组成部分。研究表明，调整超声振幅和频率可以提高加工表面质量[8-9]。合理设计超声振动系统对超声加工的发展与应用具有重要意义。在实际超声加工中，变幅杆的输出端面有负载，传统设计时忽略刀具负载影响，降低了设计及计算难度，却使得超声振动系统实际谐振频率与理论值产生偏差，且随加工条件的改变造成振动系统失谐，不利于充分发挥超声加工优势，而考虑刀具负载可取得较好的设计效果[10-12]。

范国良等[13]利用超声技术加工深小孔时，发现当工具杆直径(或面积)远小于与之连接的变幅杆输出端直径(或面积)，即二者直径之比小于0.30(或面积比约小于10%)时，工具杆能独立于变幅杆单独共振，并将此现象称为局部共振现象。该现象的发现简化了超声振动系统设计，摆脱了按半波长整数倍进行设计的概念。之后，很多学者又进行了研究：赵波等[14]在超声珩磨复杂声学系统的研究中发现，若将挠性杆- 油石座振动子系统看作一个单独共振体，复杂系统采用局部共振原理来设计，则只要保证挠性杆- 油石座- 振动圆盘相互的截面比值不大于10%，即可满足局部共振条件且能获得良好振动效果。徐可伟等[15]研究了简单变幅系统的局部共振设计方法。应崇福等[16]在动力吸收器的原理推导中得出在变幅杆与工具杆的联接处总会出现位移节点的结论。郑建新等[17]在振动钻削研究中从理论上得到了联接处总会出现位移节点的原因。周光平等[18]提出局部共振是声学系统在谐振状态下的一种特殊情况。鲍善惠[19]提出局部共振是变幅系统与工具杆在弱耦合时的一种特殊表现。局部共振设计时考虑工具杆，可完全避免刀具本身负载对系统谐振频率的影响，但利用局部共振如何设计声学振动系统鲜有报道。

本文利用局部共振原理将变幅杆和工具杆均作为子系统进行单独设计，以避免刀具负载对谐振频率的影响。推导了组合系统的频率方程，进而确定了振动系统的尺寸，对振动系统进行了仿真分析并进行了试验验证，为超声振动系统设计提供了一种参考方法。

1 理论分析

1.1 局部共振系统的频率方程

如图1所示，将变幅杆作为子系统A，工具杆作为子系统B. 图1中：FA为A系统变幅杆与工具杆的连接处所受的力；FB为B系统工具杆与变幅杆的连接处所受的力；XA、XB为位移坐标；Rl、Rs分别为A系统变幅杆大端面和小端面半径；Lf、Lt、Le分别为A系统变幅杆首段、过渡段和末段长度。

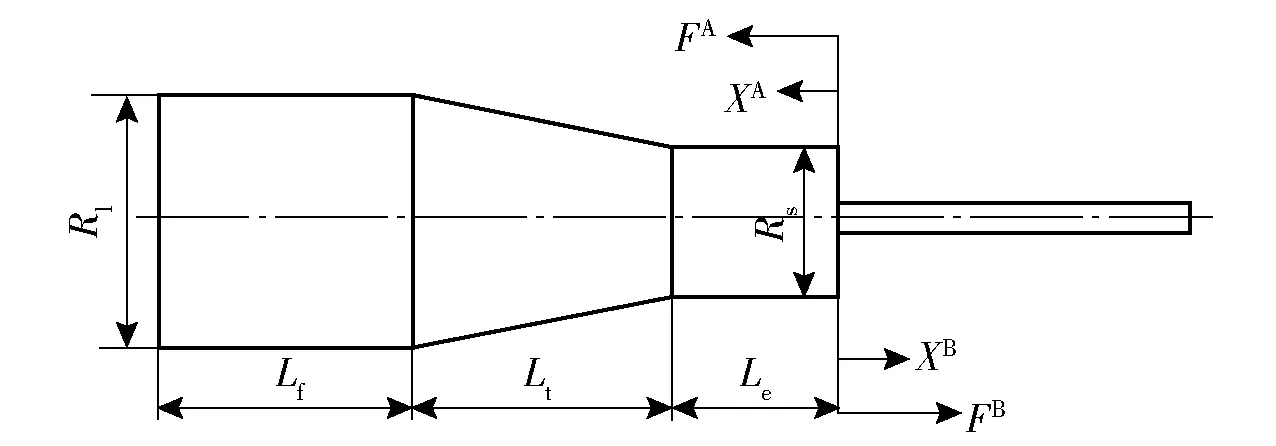
图1 超声振动系统模型Fig.1 Ultrasonic vibration system model

系统所受的力与位移的比值称为位移阻抗，子系统的位移阻抗为

(1)

整个系统在连接处的总阻抗为子系统阻抗值之和[15]：

Z=ZA+ZB，

(2)

组合系统谐振状态下Z=0，即子系统A与子系统B的阻抗和为0.

子系统A的设计长度为1/2波长，变幅杆制作材料选用疲劳强度较高且易加工、振动传递效果较好的45号钢。材料参数如表1所示。

表1 45号钢材料参数

变截面杆纵向振动的波动方程为

(3)

式中：ε为质点位移函数；x为质点坐标；S为变幅杆横截面积；k为圆波数，k=ω/c，ω为圆频率。对于圆锥过渡复合变幅杆，频率方程为

(4)

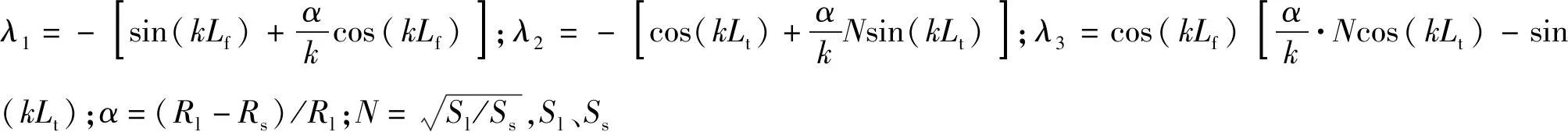
变幅杆大端需与换能器相匹配，取大端半径Rl=15 mm、小端半径Rs=7 mm. 将45号钢的材料参数代入(4)式，经计算得首段长度Lf=30 mm，过渡段长度Lt=35 mm，末段长度Le=17 mm.

细长的等截面工具杆局部共振出现在工具杆的直径(或面积)小于与之相接的变幅杆输出端直径(或面积)时，即在直径比约小于0.30(或面积比约小于10%)时发生局部共振[13]。子系统A的输出端半径7 mm，故可取子系统B中的工具杆直径为3 mm，以使组合系统发生局部共振。

单自由度机械振动系统的位移阻抗为

k0-ω0m0+jω0c0,

(5)

式中：k0为系统弹性系数；ω0为系统固有频率；m0为系统质量；c0为系统阻尼系数。

将系统A等效为如图2所示的单自由度振动系统，即不计阻尼cA时，子系统A的位移阻抗：

ZA=kA-ωAmA,

(6)

式中：kA为变幅杆弹性系数；ωA为变幅杆固有频率；mA为变幅杆质量。

图2 子系统A动力学模型Fig.2 Dynamics model of Subsystem A

子系统B为一圆柱形工具杆，其阻抗[15]为

ZB=-EBdBkBtan(kBLB)，

(7)

式中：EB为工具杆弹性模量；dB为工具杆直径；kB为组合系统的圆波数，亦是工具杆一端固定另一端自由时的圆波数；LB为工具杆长度。

由此可得振动系统的频率方程为

kA-ωAmA+EBdBkBtan(kBLB)=0.

(8)

由(8)式可以看出：子系统A的位移阻抗是固定不变的，当工具杆材料及面积确定时，子系统的位移阻抗仅与设计频率及长度有关；当工具杆长度发生改变时，仅需改变设计频率值即可使频率方程成立。由此从理论上解释了工具杆发生磨损后仅需调节激振频率振动系统仍能取得良好振动效果。

本文取工具杆与变幅杆的材料均为45号钢，设计频率为40 kHz，将参数值代入频率方程(8)式，经数值分析软件MATLAB进行计算，得出LB=32 mm.

1.2 仿真验证

利用有限元分析软件ANSYS对设计的变幅杆进行仿真分析，定义材料参数如表1所示，对其进行模态分析并提取纵振模态，仿真结果如图3所示。由分析结果可知，所设计变幅杆的谐振频率为35 083 Hz,与理论值仅相差83 Hz，变幅杆子系统A设计正确。

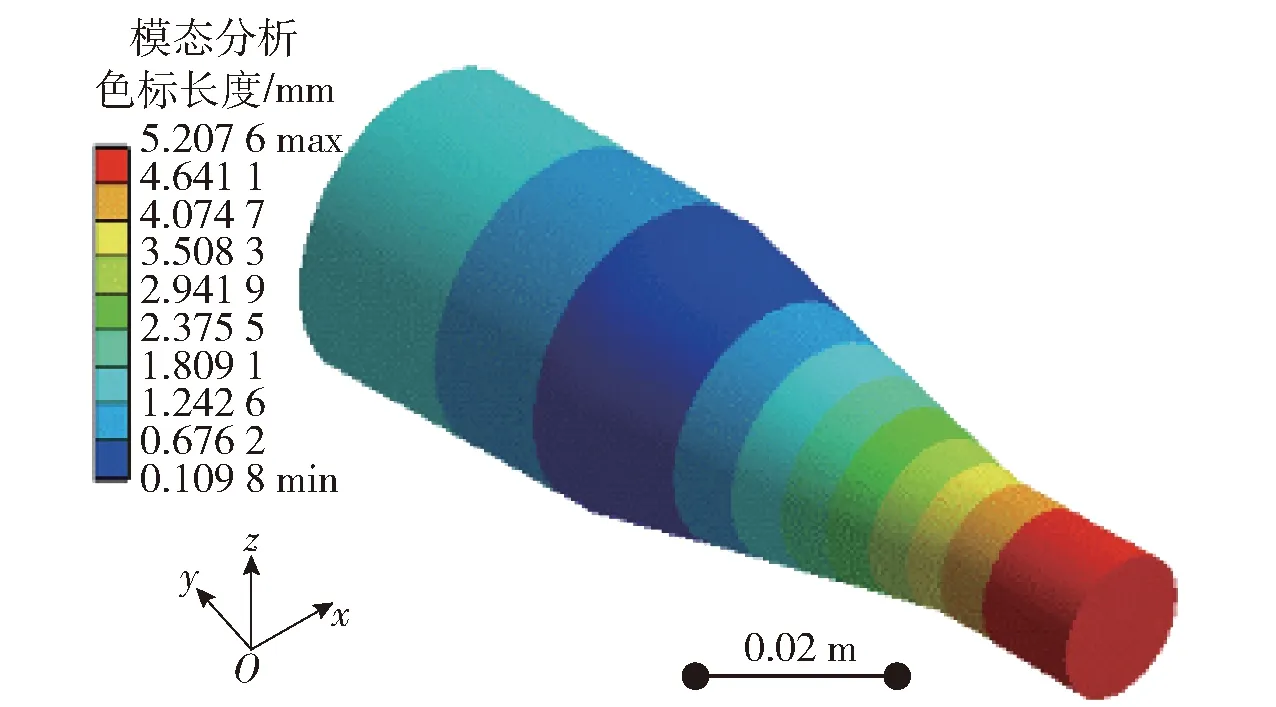
图3 子系统A模态分析结果Fig.3 Modal analysis results of Subsystem A

将所设计的局部共振系统以及一端固定、一端自由状态下的子系统工具杆进行模态分析，分析结果如图4和图5所示。

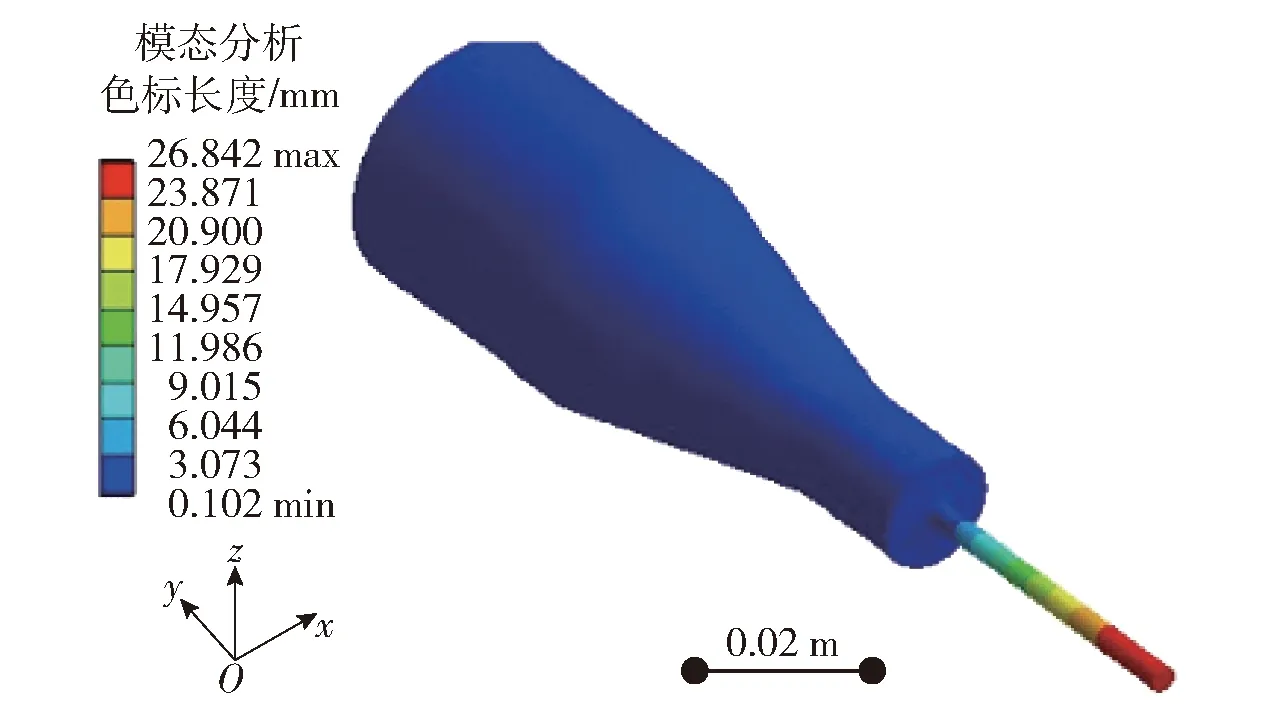
图4 振动系统模态分析结果Fig.4 Modal analysis results of vibration system

图5 子系统B模态分析结果Fig.5 Modal analysis results of Subsystem B

由图4及图5可看出，超声振子的谐振频率为40 440 Hz，工具杆在一端固定、另一端自由状态下的谐振频率为39 539 Hz，二者接近相等且与设计值偏差均小于1.25%，表明设计过程合理且准确；子系统B发生局部共振时，系统谐振频率在工具杆固有频率附近，此时整个系统依然是全谐振状态，因此局部共振可理解为系统谐振时的特殊情况。

为得到振动系统轴向不同位置的振动位移，在变幅杆输入端施加1 μm位移振动，激振频率为超声系统谐振频率进行谐响应分析，分析结果如图6所示。

图6 振动系统轴向位移分布Fig.6 Axial displacement distribution of vibration system

从图6中可以看出，变幅杆(长度0～82 mm)的振幅相对于工具杆的振幅较小，变幅杆与工具杆连接处位移接近于0 mm，工具杆起到振幅放大作用，达到局部共振设计目的。

实际加工中，变幅杆需添加与刀柄相连的法兰盘，由图6所示的谐响应分析结果可知，节点位置与输入端距离相差27 mm，取法兰盘中间平面位于该位置、法兰厚度为6 mm、直径60 mm，对振动系统进行模态分析，结果如图7所示。从图7中可见，添加法兰盘后系统的谐振频率上升至40 516 Hz. 原因是添加法兰盘后，子系统A的质量发生改变，从而造成频率发生改变，但偏差量较小，与设计频率的相对偏差值仅有1.3%，在误差允许范围内。

图7 振动系统模态分析结果Fig.7 Modal analysis results of vibration system

综上所述，基于局部共振理论的超声振动系统设计完成，并通过有限元仿真进行了验证，故按照局部共振原理来设计振动系统是可行并且正确的。该系统设计完成后，系统频率不受刀具负载的影响。

2 子系统A在负载下的频率变化

2.1 子系统A在负载下的频率方程

图8 复合变幅杆等效T形网络Fig.8 Equivalent T-shaped network of composite horn

变幅杆在纯抗性负载下的频率方程[21]为

(9)

当负载Z=0时，频率方程可化为上述无负载下的频率方程(4)式。由此可知，空载下的频率方程是抗性负载下的频率方程特殊情况。

图9 Le不同取值下的谐振频率变化曲线Fig.9 Variation diagram of resonance frequency at different lengths of Le

同时可发现变幅杆长度Le减小，共振频率随抗性负载的变化越敏感。例如当容抗负载足够大时，Le=17 mm的变幅杆谐振频率值与设计值相差41 471 Hz，Le=33 mm的变幅杆谐振频率值与设计值相差4 393 Hz，二者相差约9.44倍。因此Le的长度对于负载下的共振频率影响较大，为尽量减小抗性负载对谐振频率的影响，设计变幅杆时，应增加Le的值。

2.2 刀具负载对谐振频率的影响

如果刀具形状简单，且横向尺寸小于1/10波长、长度小于1/4波长，则工具杆对变幅杆的影响可以看作质量抗性负载。忽略刀具装夹的影响，取刀具材料与变幅杆材料相同，均为45号钢。变幅杆添加直径为6 mm、8 mm的刀具，采用模态分析方法提取刀具不同长度下的纵向振动谐振频率值，模态分析图与不同刀具参数下的谐振频率曲线图如图10和图11所示。

图10 变幅杆施加刀具负载的模态分析结果Fig.10 Modal analysis of horn after applying a tool load

图11 不同刀具参数下的谐振频率变化曲线Fig.11 Resonance frequency curves under different tool parameters

由图11可见，随着刀具长度的增加，振动系统的谐振频率逐渐减小，当刀具伸长量不变时，谐振频率随着刀具直径的增加而减小，刀具负载应为感抗负载。当直径为φ8 mm的刀具长度为32 mm时，其谐振频率与理论设计值偏差在25%以上，频率差值较大，局部共振设计的振动系统则不受刀具负载的影响，仿真结果与理论值的相对偏差在2%以内，具有明显的优越性。

3 试验

3.1 局部共振系统的试验验证

机械加工出按局部共振理论设计的变幅杆，利用PV70阻抗分析仪进行阻抗频率分析，阻抗分析现场及测量结果如图12、图13所示。

图12 阻抗分析测量现场Fig.12 Impedance analysis and measurement setup

由分析结果可知：变幅杆实测谐振频率约39 530 Hz，与设计频率相差约500 Hz. 这是因为：1)仿真时未考虑变幅杆与换能器的连接问题；2)加工材料特性值与模态分析定义值不能完全相同。

从整体结果来看，实际频率值与工具杆的仿真固有频率值非常接近，与设计频率值的相对误差小于3%，且导纳圆圆度较好，电导曲线正常，电阻值仅有20 Ω，振动系统的机械品质因数较好。即系统电声转化效率高，表明所设计变幅杆的尺寸及其结构十分合理。

利用日本基恩士公司生产的KEYENCELK-G10型激光位移传感器进行振幅测试，振幅值可达18 μm，测量结果如图14所示，图中纵坐标单位为mm.

由图7所示的仿真分析结果可知：系统发生局部共振时，工具杆起振幅放大作用，变幅杆振动位移较小。激光测振仪难以对系统各处的振幅进行测量，故利用测振仪无法得到系统的振动位移分布规律。但是振动系统某处的振动位移越大，其应力就较大，温度相应越高，为得到所设计振动系统不同位置的振动情况，采用美国FLIR公司生产的FLIRE5红外热像仪对其进行温度测量，测量结果如图15所示。

图15 红外热像仪测试结果Fig.15 Test results of infrared thermal camera

从图15中可以看出，振动系统的发热主要集中在换能器的压电陶瓷处以及工具杆处。压电陶瓷是超声振动的激励处，且与电源相连，将电能转换为机械能并伴随着能量损失，故温度较高。变幅杆整体温度相对于工具杆较低，可以推测变幅杆振幅相对于工具杆较低，工具杆起到振幅放大的作用，与上述谐响应分析结果相同，进一步验证了采用局部共振设计的正确性。

3.2 力负载下的对比试验

抗性负载由力负载引起，为探究局部共振系统及单独设计的系统在力负载下谐振频率的变化规律，制作了特定工装进行了模拟分析试验，试验测量现场如图16所示。

图16 模拟试验测量现场Fig.16 Simulation test measurement site

试验前机械加工一个圆锥过渡复合变幅杆即传统方法下仅对变幅杆进行设计的声学振动系统，变幅杆材料为45号钢，采用与45号钢特性相近的高速钢刀具。调节刀具伸长量，使其在弹簧夹头中的夹持长度合适，以使声波有效传递。将变幅杆法兰盘置于工装上表面，工装由锁刀座支撑，锁刀座下部放置由日本Kistler公司生产的9257B型压电式三向测力仪传感器，整个装置放置于万能铣床工作台上，压力杆连接在主轴上且位置固定不动，转动手轮调节机床工作台高度，给刀具施加不同大小的轴向力。为减弱工装对测量的影响，在法兰盘与工装连接处设有阻止振动传递的垫片，振动系统谐振频率由杭州泛索能超声科技有限公司生产的PV520A阻抗分析仪进行测量。由于45号钢强度有限，仅施加至一般加工时刀具所受的轴向力大小，本文取500 N，测量结果如图17所示。

图17 谐振频率随力负载变化曲线Fig.17 Resonance frequency vs. load force

由图17可见：单独设计与按照局部共振设计的振动系统，其谐振频率均先随力负载的增大而增加，而后趋于稳定；力负载下的谐振频率变化与容性负载下的频率变化趋势相同，但是负载力为500 N时，局部共振系统的频率增加值约占传统方法设计时的25%，故采用局部共振理论设计的振动系统在力负载下更加稳定。

3.3 超声辅助钻削试验

试验平台搭建在沈阳机床厂生产的VMC850E三轴立式加工中心上，测力仪固定在加工中心的工作台上，浙江天一机床附件公司生产的三爪卡盘被固定于测力仪上，将超声专用刀柄与主轴相连，上述局部共振系统中的子系统B由直径3 mm的钻头代替，进行TC4钛合金钻削试验。仅对轴向力进行采集，试验现场如图18所示。试验方案如表2所示，其中：1号试验采用局部共振系统，2号试验采用传统超声系统，3号试验采用普通加工。

图18 钻削试验现场Fig.18 Drilling test setup

试验序号转速/(r·min-1)进给速度/(mm·min-1)振幅/μm1号30002042号30002043号3000200

由图19可知，与普通钻削相比，超声振动钻削可使轴向力降低约20%，但超声辅助钻削时轴向力具有波动性。与传统超声系统相比，局部共振系统在钻削时轴向力的波动较小。究其原因：由于超声振动的施加，使得轴向负载力发生变化，又从模拟试验可知超声系统在力负载下，谐振频率会升高，而局部共振系统的频率偏差量较小；因频率对负载力也具有反作用，故引起局部共振系统的轴向力波动较小，从而也表明采用局部共振理论设计可提高超声系统的稳定性。

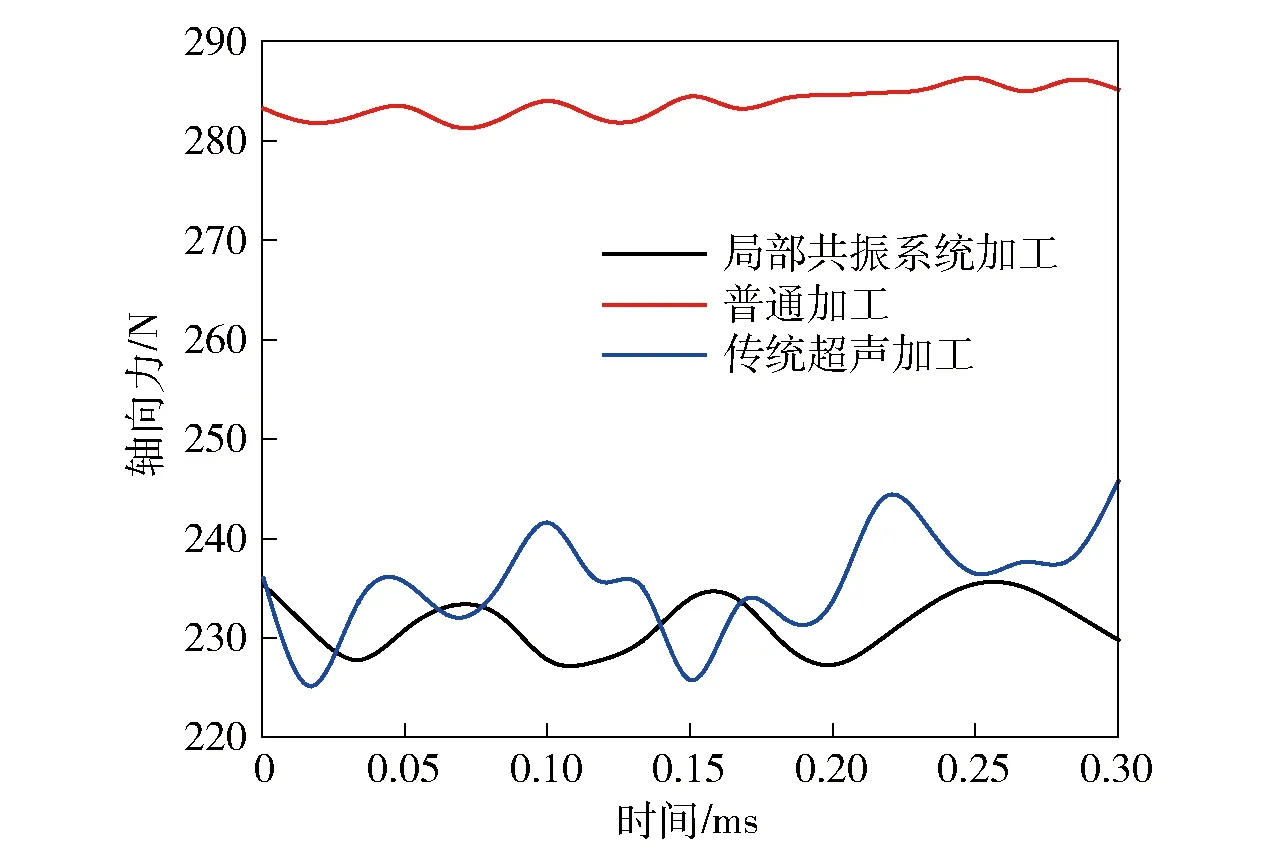
图19 不同加工条件下的轴向力对比图Fig.19 Comparison of axial forces under different processing conditions

将加工完成的试件放置在日本基恩士公司生产的VHX-2000型超景深显微镜下进行观察，由图20所示的观察结果可知，局部共振系统与传统超声加工系统的制孔效果相差较小，局部共振系统加工出的孔的边缘处略显光滑，而采用普通加工制出的空有明显毛刺。故超声振动的施加有效抑制了毛刺的产生，又因局部共振系统更加稳定，导致加工效果相较于传统超声加工较好。

图20 不同加工条件下的结果对比图Fig.20 Comparison of machining results of under different machining conditions

4 结论

本文推导了局部共振状态下的频率方程，为超声振动系统设计提供了新的方法。设计一个带有复合变幅杆的振动系统，并进行了试验探究。得出结论如下：

1)子系统A在抗性负载下的容抗越大，系统共振频率越大；感抗越大，共振频率越小。设计变幅杆时增加Le值，可减弱负载影响。

2)当φ8 mm工具杆长度为32 mm时，传统声学系统谐振频率值与设计频率值的相对偏差达25%以上，而采用局部共振系统则不受刀具本身负载影响。力负载下，系统谐振频率将升高，轴向负载力为500 N时，传统声学系统的谐振频率与空载时的频率偏差值为1.15 kHz，而局部共振系统的频率偏差值小于300 Hz，稳定性明显较高。

3)局部共振系统在实际加工中力的波动性小于传统超声系统，且有效抑制了孔壁毛刺的产生，其加工效果相较于普通加工及传统超声加工方式均较好。