焓湿向量空间及空调系统实际性能计算

戢坤池 庄迪君 王 楠 高秀芝 王志华 王沣浩

焓湿向量空间及空调系统实际性能计算

戢坤池1庄迪君2王 楠1高秀芝1王志华1王沣浩1

（1.西安交通大学建筑节能研究中心 西安 710054；2.南京平日制冷科技有限公司 南京 211300）

针对空调系统的实际运行冷量与室内热湿负荷不匹配的问题，基于焓湿图建立了焓湿向量空间，将空调系统传统设计计算方法转化为焓湿向量计算。定义了负荷向量和空调机组函数，提出了迭代分析算法，在空调房间热湿负荷不变的前提条件下，于设计初期可理论预测出不同室外环境下空调系统的实际性能，从而省去了实验测试。并利用该算法对高温和高湿工况进行了空调实际性能计算。最后将实测数据和迭代算法计算结果作误差分析，相对误差在4%以内，验证了该算法具有较高的准确度。

焓湿向量空间；迭代分析算法；空调系统实际性能计算；准确度验证

0 引言

当前，由于流体管网输配的滞后性、空调末端设备换热效率的不稳定性、设备控制调节的延时性以及建筑人员密度随时发生变化、建筑门窗开启状况的变化等因素的影响，空调系统的传统设计方法中存在系统实际运行冷量与室内热湿负荷在时间和数值上不匹配的问题[1,2]。此外，空调系统传统设计方法的室外干球温度采取的是夏季室外空气历年平均不保证50小时的干球温度，该温度在如今全球气候变暖、恶劣天气频发的背景下，与实际室外温度已有偏差，难以保证利用传统方法设计出的空调系统适用于全年的室外环境[3]。并且，传统设计通常采用增加10%到20%的安全系数使得空调系统的容量扩大1.1到1.2倍，将此计算结果作为空调容量选型的依据，以适应室外环境的变化[4]。但采用安全系数的方法使得空调冷量偏大，加剧了空调实际运行冷量与室内热湿负荷不匹配的问题。

利用传统方法设计选型的空调系统存在实际运行冷量和室内热湿负荷不匹配问题的内在原因在于空调系统的实际运行过程比理论更加复杂，设计人员难以在设计阶段实现精确且低成本地预测出空调系统在全年气候环境条件下运行时的室内稳定状态点和实际运行冷量[5]。

从设计方法的角度来讲，目前传统空调系统的设计方法没有具体的数学算法作为设计依据，仅是通过计算步骤的累积形成设计方法，在此基础上获取空调系统设计的近似解，因此本质上属于数值计算方法。而为了计算空调系统在实际工况下运行的室内稳定状态点和实际运行冷量，则需要通过解析法分析整个设计过程，以获取空调系统设计方法的解析解[6]。而解析法的第一步，就是在数学平面上建立坐标系，把已知点轨迹的几何条件转化为代数方程。

根据以上分析，本文基于焓湿图建立了焓湿二维坐标系，构造了焓湿向量空间（-Vector Space），将传统借助焓湿图作图求点进行空调设计的方法转化为焓湿向量计算，并在焓湿向量空间的基础上，提出了一种预测空调系统实际运行性能的迭代算法。在空调房间热湿负荷不变的前提条件下，利用该算法可在设计初期预测出空调系统在不同室外环境下运行时的室内稳态点和实际运行冷量，为判断该空调系统在恶劣工况下是否符合舒适性的要求提供依据，解决了利用传统设计方法难以预测空调实际冷量的问题，从而省去了实验测试。利用该算法能有效地改善空调实际冷量与室内热湿负荷不匹配的问题，避免能源浪费；同时也能节省空调系统实验测试成本，且使设计的空调系统更加符合室内热环境的舒适性要求。

1 焓湿向量空间

在焓湿图上，将空气状态点的焓值和含湿量均为0值作为零点，过零点垂直于等焓线的轴为轴，过零点垂直于等含湿量线的轴为轴，建立起-二维坐标系，构造出焓湿向量空间[7]，如图1所示。焓湿图上的每个空气状态点由坐标（，）唯一确定，则空气处理过程可由空气始末状态点的连线，即向量表示。其中焓的单位为kJ/kg，含湿量的单位为g/kg。

定义负荷向量：

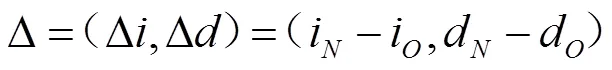
新风负荷向量：

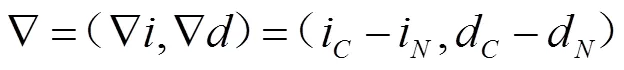
式中：代表室内状态点，代表送风状态点，代表混合状态点。将空调机组中的空气由进风点到出风点的处理过程视为一个函数F，依据负荷向量和空调机组函数，建立了计算空调系统实际运行性能的分析算法。下文以一个空调系统设计实例来阐述焓湿向量空间的算法。

一次回风空调系统，室外设计计算干球温度D=35℃，湿球温度W=28℃；室内设计干球温度D=25℃，相对湿度R=50%；室内冷负荷=50kW，湿负荷=5g/s；新风比10%；无回热。空气处理过程如图1所示。详细计算结果见表1、表2。

图1 焓湿向量空间及空气处理过程

表1 空气状态点在焓湿向量空间中的表示

注：O点是过N点作室内热湿比线与相对湿度95%线的交点。

表2 空调系统参数计算结果

图1中由室外新风与室内回风的混合状态点到送风状态点的过程为空调机组处理混合空气的过程。对于选型确定的空调机组，当点确定之后，仅有唯一的点与之对应，即到的过程是个一一映射的过程，可视为一个函数，则空调机组处理混合空气的过程可用=（）来表示。

进而通过焓湿向量空间、负荷向量△和空调机组函数三个数学实体可将空调系统传统设计方法中出现的空气状态点、热湿负荷和空调系统设备转化为数学表示，这对构建空调系统实际性能计算的分析算法具有显著的意义[8]。

若室外环境参数发生变化，由表2参数选型的空调系统在实际运行时，如何预测室内稳定状态点和该空调系统的实际冷量？

传统利用焓湿图的设计方法难以计算空调系统的实际冷量，因此在现实中通常采用的方法是对该空调系统的室内状态点和实际运行冷量进行实验监测来获取空调实际性能，但这种方法需要较高的测试成本。针对上述问题，本文提出的空调系统性能计算的迭代分析算法，在空调房间热湿负荷不变的前提条件下可从理论上预估出空调系统在不同室外环境下的实际运行性能。

2 迭代分析算法

在焓湿向量空间、负荷向量和空调机组函数的基础上，以一次回风空调系统为例，本文提出了在空调房间热湿负荷不变的前提条件下，能够从理论上预估出空调系统在不同室外环境下的运行性能的迭代分析算法，表达式如下：

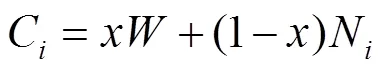
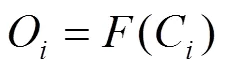
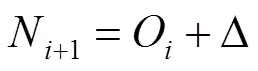
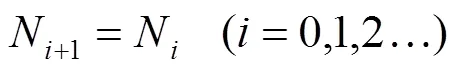
式中：为新风比，为空调机组函数，△为负荷向量。这是一个迭代分析算法，式（3）～（5）为计算式，式（6）为收敛条件，即前后两次室内状态点的计算结果相等时认为迭代达到收敛。算法的迭代初值可取室内稳定状态点的预估值。

上述式（3）～（5）可简化为如下表达式：

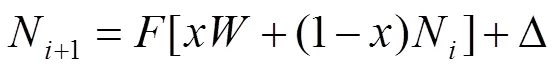
回到前文的问题，要预测空调系统在不同室外环境参数下的室内稳定状态点和实际性能，只需把室外点W的焓湿坐标和不同室外条件下计算的负荷向量代入式（7）中进行迭代计算，当计算结果收敛时，就可得到室内稳态点N和送风点状态O，进而可计算出空调实际冷量。迭代计算过程见图2。进而在设计阶段仅通过数学迭代算法预估出不同工况下的室内稳定状态点和空调实际性能，就可判断出该空调系统在恶劣工况下是否满足舒适性的要求。若不满足，可以采取扩大或减小风量的措施，改变负荷向量的大小，重新进行迭代计算，直到计算的室内稳定状态点符合舒适性要求，此时的风量为空调实际运行所需调控的风量。

接下来对迭代分析算法做几点进一步的阐释和说明：

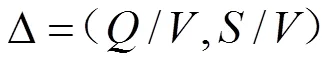
（2）当室外环境参数给定后，室内的热湿负荷以及送风过程的热湿比线也已经确定，因此负荷向量的大小仅与空调风量相关。在迭代计算过程中，因此在空调房间热湿负荷和新风量不变的前提条件下，迭代过程中负荷向量△不变。

（3）当前后两次迭代计算的室内状态点相等时，即认为迭代达到了收敛。采用作图法可以证明，选定初值，经过有限次迭代，迭代均可得到收敛解。如图3所示，将常规设计的空气处理过程用虚线表示，迭代计算过程中空气状态点和处理过程的变化趋势用实线表示。从图中可以看出，（+1）与（）之间的距离随着迭代次数的增加呈递减的趋势。则经过有限次迭代计算后，点将达到一个稳态点。

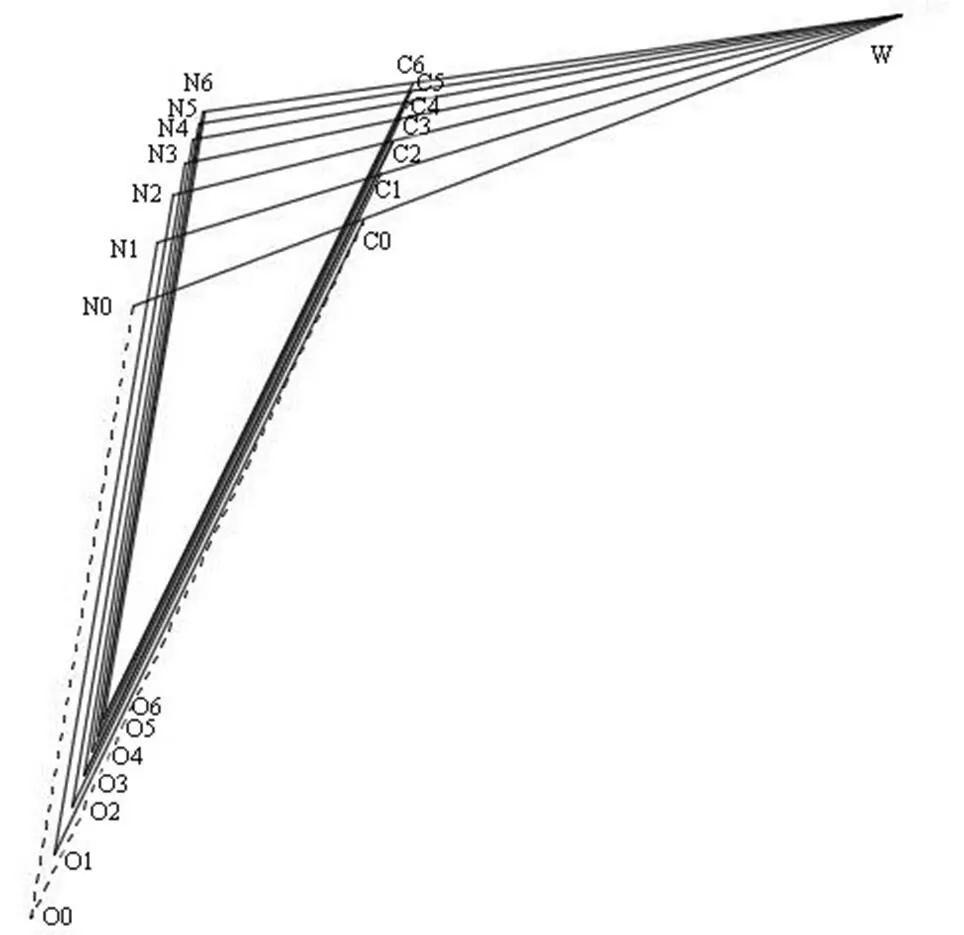
图3 迭代分析算法收敛性的证明

（4）迭代分析算法的初值要求须在室内真实稳定状态点的一定误差范围之内，即要求迭代计算的负荷向量尽可能接近实际值。

（5）不同的空调机组，其函数不同，但在空调机组选型确定之后，函数也相应确定。=（）代表的是空调机组处理混合空气的过程。本文利用数学软件Matlab仿真函数并进行模拟计算[9]，通过输入空调机组的结构参数和混合状态点的参数，输出送风点的参数，即可将空气混合过程数学化。

（6）迭代分析算法可适用于不同类型的空调系统，如由风机盘管加新风构成的空调系统，也可构造其迭代分析算法。空气处理过程见图4，其迭代分析算法的表达式为：

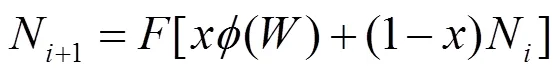
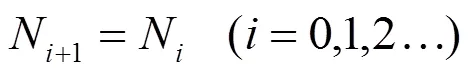
式中：为新风比，为新风机组函数，为风机盘管机组函数。

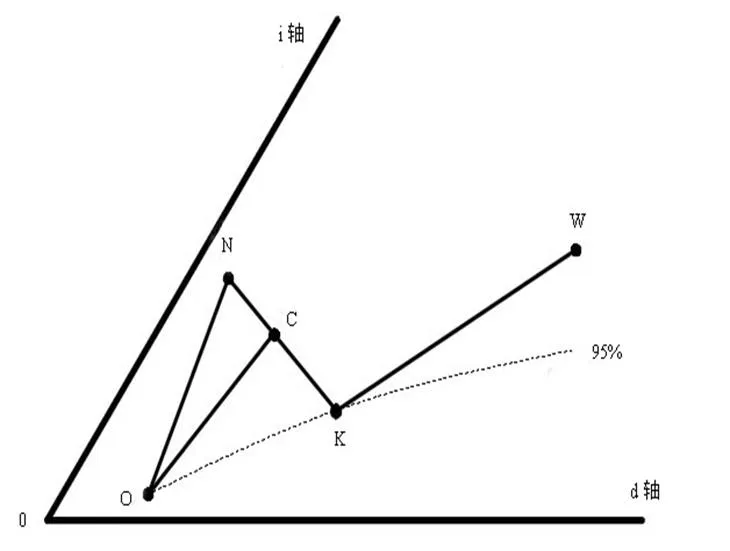
图4 风机盘管加新风的空调系统处理空气过程

3 实际应用

3.1 高温工况的空调实际性能计算

以南京某会议室在标准工况（室外设计计算干球温度34.8℃，湿球温度28.1℃）下设计及选型的由风机盘管加新风机组构成的空调系统为例，空气处理过程见图4。其中，新风机组的额定冷量1=13.75kW，结构参数见表3；风机盘管机组的额定冷量2=19.5kW，结构参数见表4。当空调系统在高温恶劣工况（室外干球温度40℃，相对湿度70%）下运行时，利用焓湿向量空间理论和迭代分析算法来计算在高温工况下的室内稳定状态点和该空调系统的实际性能。

预估室内状态点为干球温度28.4℃，相对湿度57%，负荷计算结果为：室内冷负荷=17.913kW，湿负荷=1.755g/s。且新风比为0.262，总风量=1.278kg/s，由负荷向量的计算式得△=（14.02,1.37）。将高温工况下的负荷向量代入公式：

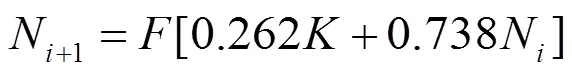
中进行迭代计算，式中：

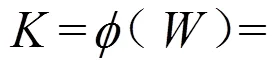
迭代计算过程见表5。由计算结果可知室内稳态点为（64.16,13.89），空调的实际性能计算结果为：高温工况下的室内稳态点的干球温度为28.37℃，相对湿度为57.5%。新风机组的实际冷量为1=15.84kW，风机盘管机组的实际冷量为2=21.27kW，空调系统的总制冷量为=37.11kW。

3.2 高湿工况的空调实际性能计算

若将上述由风机盘管加新风构成的空调系统在南京雨季（室外干球温度27℃，相对湿度90%）的室外环境下运行时，同样利用迭代分析算法，预估室内状态点为干球温度21.6℃，相对湿度61%。此时计算的室内冷负荷为=14.52kW，湿负荷=1.176g/s。风量和新风比不变，则负荷向量△=（11.362,0.92）。将该负荷向量代入式（10）再次进行迭代计算，式中：

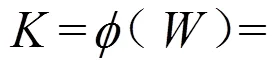
迭代计算过程见表6。由计算结果知室内稳态点为（46.782，9.80），空调的实际性能计算结果为：高湿工况下的室内稳态点的干球温度为21.67℃，相对湿度为60.8%。新风机组的实际冷量为1=10.19kW，风机盘管机组的实际冷量为2=14.92kW，空调系统的总制冷量为=25.11kW。

表3 新风机组结构参数

表4 风机盘管结构参数

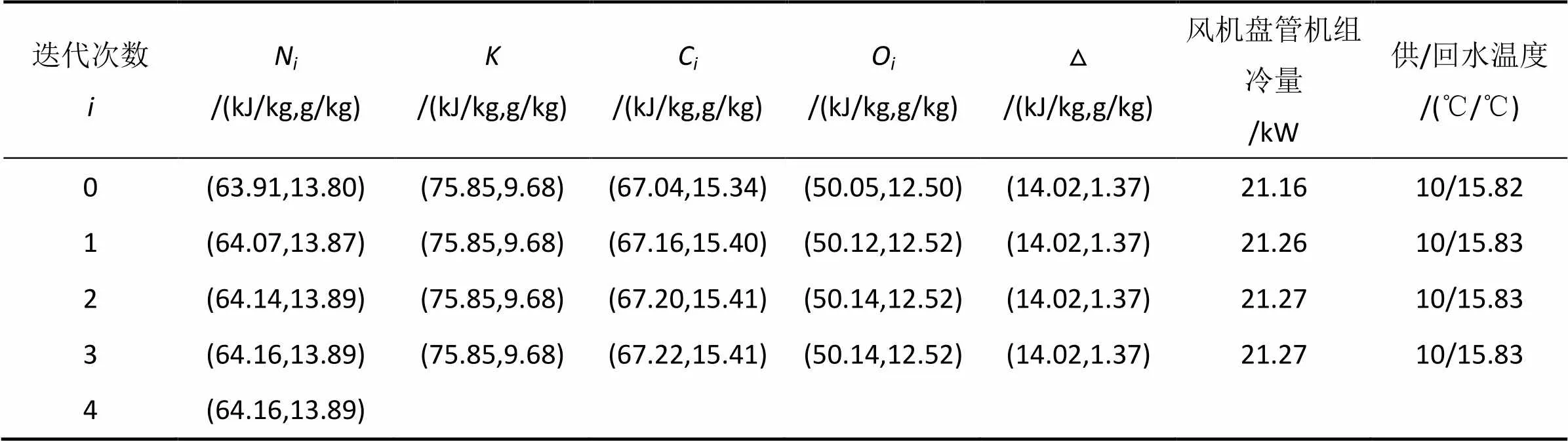
表5 高温工况迭代计算过程

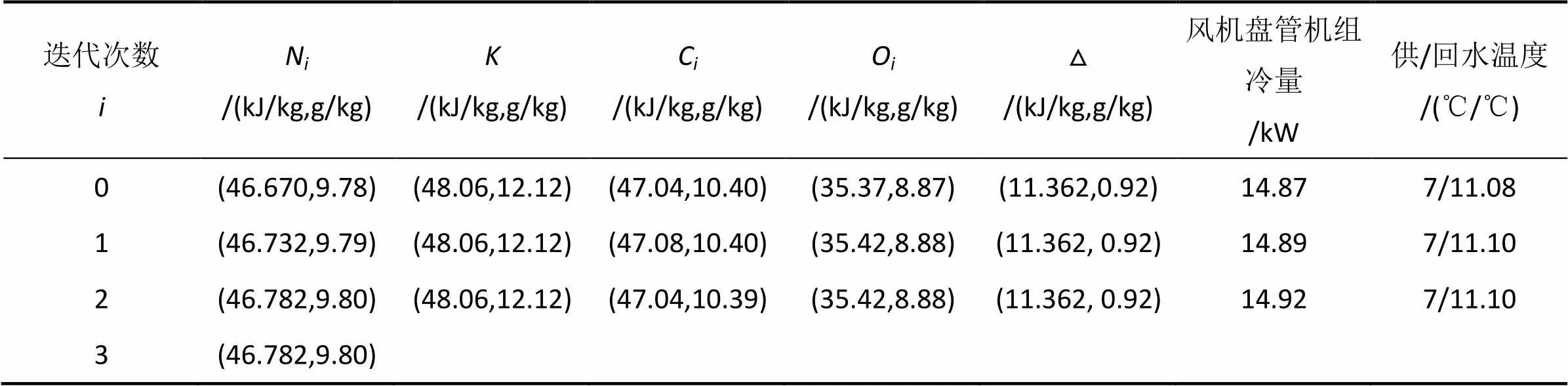
表6 高湿工况迭代计算过程

4 算法准确度验证

4.1 函数F编程准确度的验证

本文中提出的空调机组函数是借助Matlab软件编程进行仿真模拟计算。模型的仿真模拟计算过程为：输入参数为空调机组结构参数和盘管入口空气状态点，通过设定冷冻水供水温度，模型的输出参数为冷冻水回水温度和盘管处理空气后的送风状态点，编程模拟的方法和步骤参考文献[10]。搭建实验平台，测试风机盘管的送风状态点参数和系统性能，以及实际的供回水温度。将模拟计算结果与实验测试数据做误差分析，数据见表7，分析结果见图5。由图5可知各项参数的相对误差均在10%以内，表明函数仿真模拟结果具有较高的准确度。

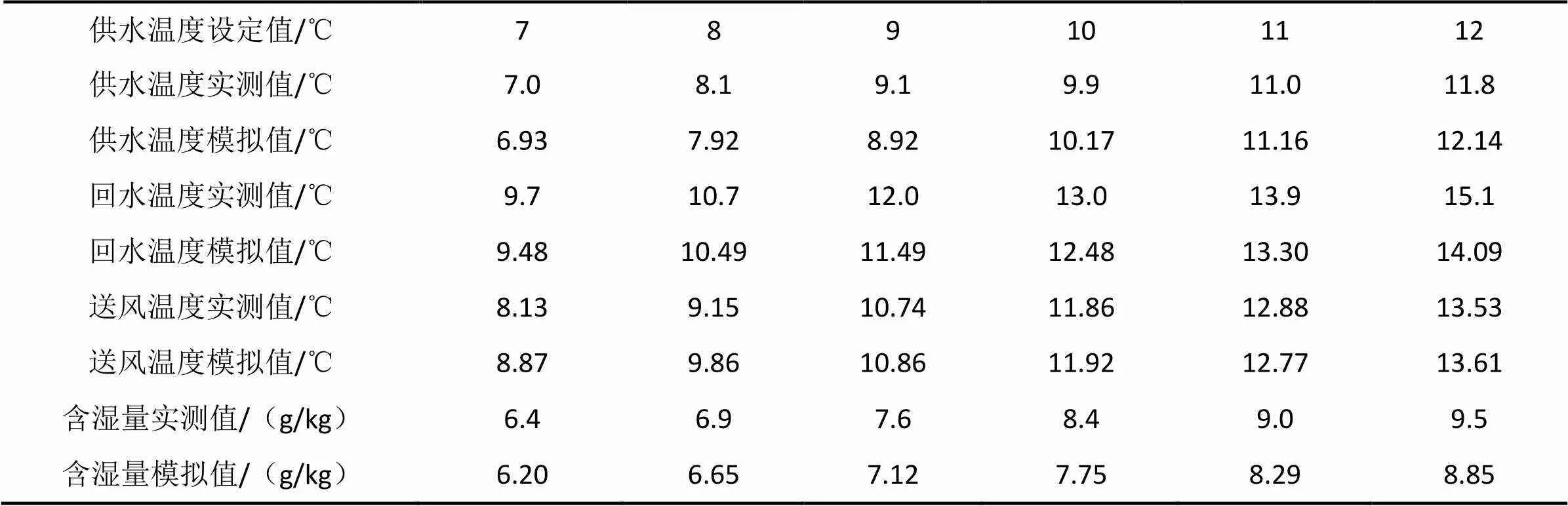
表7 编程模拟与实验测试的数据对比

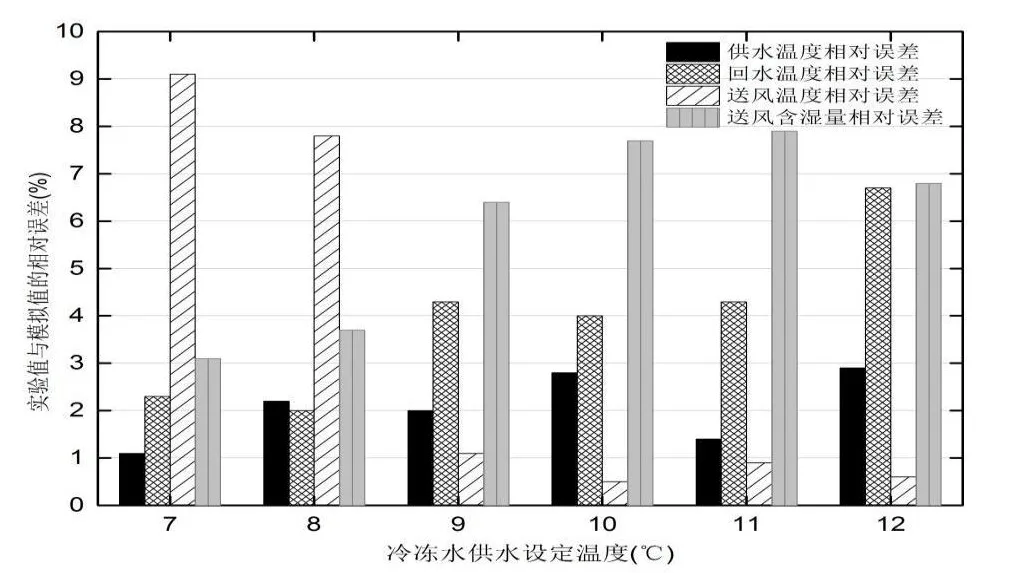
图5 函数F编程模拟结果的相对误差分析

4.2 迭代分析算法准确度的验证

以南京平日科技有限公司设计、平欧空调设备有限公司制造的供回水温度为7/15℃、型号为FP68、风量为670m3/h、额定制冷量为4.08kW的风机盘管机组为验证对象，将迭代分析算法的计算结果与合肥通用机电产品检测院的供冷工况实验测试结果（见表8）作误差分析，以验证迭代分析算法的准确度。其中，室外环境参数为干球温度34.8℃，湿球温度28.1℃，空调系统为全回风系统，新风比为0，式（7）转化为：

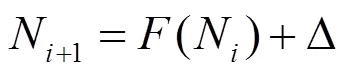
预估室内状态点为干球温度24.0℃，相对湿度54%，风量=0.22333kg/s，室内负荷计算结果为：冷负荷=3.36kW，湿负荷=0.3265g/s，负荷向量△=（15.045,1.462）。将负荷向量代入式（13）进行迭代计算，计算过程见表9。计算所得室内稳态点为（49.375,9.943），由此可知：室内稳态点为干球温度23.84℃，相对湿度54.10%。该风机盘管机组的供冷工况测试结果为：送风干球温度为13.64℃，湿球温度为12.98℃，因此测试的室内稳态点为干球温度24.66℃，相对湿度54.13%。计算结果与测试结果相比，室内稳态点的干球温度相对误差为3.34%，相对湿度相对误差为0.055%。此外，实验测试的水阻力为5.3kPa，即测试水流量为457l/h，比设计水流量442l/h大3.4%。因此在设计工况下，机组供冷量应为4.116kW，与机组设计冷量4.08kW相比，相对误差为0.88%。综合以上分析，计算结果相对误差均在4%以内，表明该迭代分析算法具有较高的准确度。

表8 FP68风机盘管供冷工况测试参数

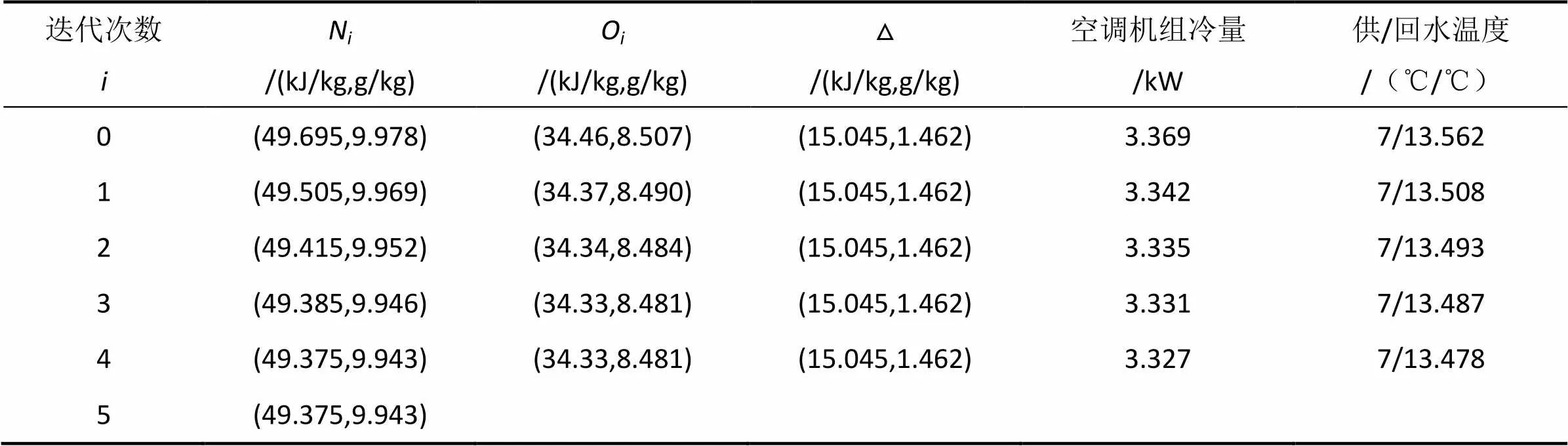
表9 全回风系统迭代计算过程

5 结论

传统的空调系统设计方法，由于缺少相应的数学算法作为设计依据，因此无法获得设计方法的解析解。本文基于焓湿图，定义了焓湿向量空间，在此向量空间基础上定义了负荷向量和空调机组函数，提出了迭代分析算法。利用该算法，在空调房间热湿负荷不变的前提下，可以计算出空调系统在任何室外环境参数下的室内稳定状态点和实际冷量，可在设计初期从理论上预测出不同室外环境下空调系统的实际性能，解决了利用传统设计方法难以预测空调实际冷量的问题，故省去了实验测试，并且能有效改善空调系统实际运行冷量与室内热湿负荷不匹配的问题。

迭代分析算法中的负荷向量应当由室内最终稳定状态点所对应的室内热湿负荷与空调机组风量的比值求得。从高温和高湿恶劣工况下的空调性能计算中可知，在取迭代初值时，预估的室内状态点不同，负荷向量就不同，迭代计算结果也会产生差异。因此在利用迭代分析算法时，要求预估室内状态点，也就是迭代初值，须在室内真实稳定状态点的一定误差范围之内，即确保迭代计算的负荷向量接近实际值，此时用于迭代计算的负荷向量才有实际代表意义。

本文基于焓湿向量空间提出的空调实际性能算法，不仅为解决实际工况下的空调系统性能预测问题提供了思路和方法，还为一些室内温湿度要求较高的空调系统的设计、优化和改进提供了理论基础，具有较广的应用拓展。如医院的净化空调系统，利用焓湿向量空间理论和空调性能迭代算法，可以较为精确地计算出室内的稳定状态点，同时可提高冷冻水系统的供回水温度，避免了传统净化空调系统运行中出现的再热问题，进而可将相应的自控系统简单化。

[1] 沈锡骞,沈士圣.商业建筑空调节能设计探讨[J].制冷与空调,2017,17(6):82-88.

[2] 刘芳,刘芳,马晓雯.深圳市酒店建筑空调系统能耗现状与节能分析[J].制冷与空调,2016,16(4):52-56.

[3] 陈友明.空调冷负荷计算方法的发展现状与挑战[J].暖通空调,2017,47(3):1-7.

[4] 袁建新,谷炳龙.多联机系统设备选型高容量指标的疑惑[J].暖通空调,2016,46(9):84-87.

[5] 孙育英,王丹,王伟,等.空调运行负荷预测方法的研究综述[J].建筑科学,2016,32(6):142-150.

[6] 姜海波,赵云鹏,程忠庆.解析法及其在复杂问题研究中的地位和作用—以风力机气动设计为例[J].系统科学学报,2014,(1):56-59.

[7] Gatley D P. Psychrometric Chart Celebrates 100th Anniversary[J]. AshraeJournal, 2004,46(11):16-20.

[8] Dhar M, Soedel W. Transient analysis of a vapor compression refrigeration system[C]. Proceedings of the 15th International Congress ofRefrigeration. Venice, Italy, 1979:1031-1067.

[9] 丁国良,张春路.制冷空调装置仿真与优化[M].北京:科学出版社,2003.

[10] 朱松勤,王弘.制冷空调蒸发器仿真的具体算法及程序设计[J].制冷与空调,2004,4(5):48-51.

I-D Vector Space and Actual Capacity Calculation of Air Conditioning System

Ji Kunchi1Zhuang Dijun2Wang Nan1Gao Xiuzhi1Wang Zhihua1Wang Fenghao1

( 1.Centre for Building Energy Conservation of Xi’an JiaoTong University, Xi’an, 710054;2.Nanjing Pingri Technologies Co., Ltd, Nanjing, 211300 )

To solvethe problem that the actual refrigerating capacity of air conditioning system mismatches the indoor heat and humidity load, this paper establishes the-vector space based on the psychrometric chart and transforms the conventional design process of air conditioning system into the calculation of enthalpy and humidity vector. Also, the load vector and the function of air conditioning unit are defined, as well as the iterative analysis algorithm is proposed, under the condition of constant heat and moisture load in air-conditional space, it can predict the actual capacity of air conditioning system under different outdoor parameters at design stage, thus the experimental test can be eliminated. Then the actual capacity of the air conditioning system at high-temperature and high-humidity condition is calculated using this method. Finally, the error analysis of the experimental data and the calculation results is carried out, and the relative error is within 4%, which verifies the high accuracy of the method.

i-d vector space; iterative analysis algorithm; actual capacity calculation of air conditioning system; accuracy verification

TU831.3

A

1671-6612（2019）04-360-07

戢坤池（199310-），男，硕士生，E-mail：kunchiji@163.com

王沣浩（197210-），男，教授，博士生导师，E-mail：fhwang@mail.xjtu.edu.cn

2018-09-03