基于核主成分分析的空域复杂度无监督评估

张瞩熹，朱熙，朱少川，张明远，杜文博

1.北京航空航天大学 综合交通大数据应用技术国家工程实验室，北京 100083 2.中国人民解放军32751单位 3.北京航空航天大学 前沿科学技术创新研究院，北京 100083 4.北京航空航天大学 交通科学与工程学院，北京 100083 5.北京航空航天大学 电子信息工程学院，北京 100083

随着全球经济一体化的推进，世界航空运输蓬勃发展。中国航空运输产业增长尤为迅猛。2017年，中国航班执行总量超过500万架次[1]，近五年年均增长率接近10%[1-2]。航空运输蓬勃增长的同时，也给空中交通管理系统带来了严峻的挑战。当前空管系统将空域划分为若干扇区，每个扇区的交通疏导由一位管制员负责。若扇区的空域复杂度超出管制员的管制能力，则极易导致空中交通安全事件发生，例如2014年的武汉机场管制员“睡岗”事件与2016年因管制失误导致的上海虹桥机场跑道入侵事件[3-4]。因此，空域复杂度评估是保障航空交通安全运行的前提与基础。

由于影响空域复杂度的动静态因素众多(涵盖扇区/航路航线/限制区等空域要素、飞行性能/飞行任务/飞行状态等航空器要素、风/云/降水/能见度等气象要素、通信/导航/监视等设备要素)，不同因素对复杂度的影响机理不同，且因素间耦合关系极为复杂，因此空域复杂度的准确评估被公认为航空领域的挑战性问题。

针对空域复杂度评估，国内外学者提出了多种方法，这些方法可分为两类。第一类方法是从单一角度来定义空域复杂度，代表性工作包括米兰理工大学Prandini教授等提出的航班冲突概率指标[5-6]、法国国立民航大学Delahaye教授等提出的Lyapunov指数指标[7-8]，南京航空航天大学张进等提出的迫近及连携度指标[9]。此类方法往往会给出明确的复杂度计算公式，但计算角度的单一性导致对复杂度的度量较为片面。第二类方法是综合多种因素提取高层复杂度指标，代表性方法包括线性回归、机器学习。线性回归方法通过线性加权多复杂度因素获得复杂度值[10-11]，但由于因素与复杂度间非线性关联，此类线性模型往往不够准确。相比之下，机器学习模型能够构建因素与复杂度间的非线性关联[12-16]，是目前准确度较高的空域复杂度评估方法。

但是，现有基于机器学习的空域复杂度评估模型的性能严重依赖标定样本。而空域复杂度的样本标定需要空中交通管制专家在细致查看管制信息的基础上进行人工标定，获取成本很高。另一方面，由于空域静态结构与运行机理的动态演变，已有标定样本会陆续过期，当需要训练新的复杂度评估模型时，很难保证有标定样本可用。本文提出了一种不依赖标定样本的扇区复杂度无监督评估方法。首先，根据扇区复杂度样本特点，采用核主成分分析(Kernel-based Principal Component Analysis，KPCA)对包含了多种因素的高维原始样本进行非线性降维，获得最大化复杂度评估信息量的主成分。然后根据实际空管业务需求，通过对降维后样本进行定制化聚类，获得各条样本对应的复杂度等级。进一步，通过在中国西南区域4个扇区的真实运行数据集上与管制专家标定的结果进行对比，验证了本文方法的有效性。

1 算法设计

扇区复杂度无监督评估方法步骤如图1所示：首先采用KPCA从原始样本中抽取能够最大化复杂度评估信息量的主成分，然后基于所评估扇区特点按需设置聚类参数，执行针对主成分(即降维样本)的定制型聚类，获得各样本对应的复杂度等级。

图1 扇区复杂度无监督评估方法流程图Fig.1 Block diagram of unsupervised evaluation method for sector complexity

1.1 KPCA降维

影响扇区复杂度的关键因素多达数十个，各因素对于扇区复杂度评估任务的信息贡献程度不同，且耦合关联复杂，所蕴含复杂度评估知识重叠。以上特点使得在无监督条件下提取扇区复杂度评估知识非常困难。为从高维原始样本中挖掘扇区复杂度评估知识，需对样本进行降维，抽取能够准确表征扇区复杂度评估知识的主成分，降低复杂度评估难度。

主成分分析(Principal Component Analysis,PCA)是挖掘高维样本数据中主成分的常用方法[17]。然而，传统PCA的主成分提取过程是线性的，不适用于各维度间非线性耦合的扇区复杂度样本。因此本文采用非线性的PCA方法——KPCA[18]，先将原始样本非线性映射至超高维样本空间中，再由此转换至最大化复杂度评估信息量的低维子空间中，获得在统计上不相关的主成分。KPCA具体步骤如下。

首先，基于高斯核函数将原始样本映射至无限维的再生核希尔伯特空间(Reproducing Kernel Hilbert Space,RKHS)中[19-20]。令该核函数为k，某一条原始样本x被映射至RKHS后为k(x,·)。继而在RKHS中通过样本维度转换获得主成分，求解主成分的表达式为

(1)

由此，特别令V=k(X,·)W(W∈Rn×m)，则主成分VTk(X,·)=WTk(X,·)Tk(X,·)=WTK，其中，K=k(X,·)Tk(X,·)=[k(xi,·)Tk(xj,·)]1≤i,j≤n=[k(xi,xj)]1≤i,j≤n∈Rn×n为核矩阵；K中各个元素k(xi,xj)能够通过以xi和xj为自变量的明确函数式计算得到。于是，求解V的问题转化为求解W的问题：

(2)

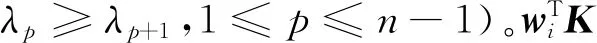
1.2 主成分聚类

通过KPCA提取出m个主成分后，若直接采用传统聚类算法处理扇区复杂度样本，则会忽略掉实际空管中不同扇区对于复杂度等级划分的差异性要求。因此，我们在聚类算法中设计了多种可调参数，能够根据所评估扇区运行特点实现按需配置。参数包括复杂度等级数量、各复杂度等级样本比例，以及初始簇中心。其中，初始簇中心为聚类算法提供不同复杂度等级簇所处样本空间位置的指导信息。基于文献[15]中附录A可知，“航空器数量”“航空器密度”这两个因素与复杂度有着强烈的正向关联，且“航空器数量”也是当前空管系统中唯一的被实际用于衡量扇区复杂度的指标。因此，我们提出参照“航空器数量”与“航空器密度”两个因素来设置初始簇中心参数。该参数设置方法为，首先对原始样本进行排序，排序标准为“航空器数量”从低到高，对于“航空器数量”因素取值相同的样本，按“航空器密度”从低到高排序；接着按照设置的复杂度等级数量、各复杂度等级样本比例参数，基于排序后样本初步划分样本的复杂度等级；然后将该样本集整体映射到高维核空间后，求解每一复杂度等级样本簇对应m个主成分的均值，作为初始簇中心。聚类算法步骤如表1所示。

表1 聚类算法步骤Table 1 Procedures of clustering algorithm

续表

2 实验结果

2.1 实验数据说明

本文基于中国西南区域4个扇区(扇区代码：GY01、GY02、KM03、CD02)在2010年7月28日8:00～24:00 GMT的运行数据进行复杂度评估实验。这一数据集拥有3 840(960分钟×4扇区)条复杂度样本，其中的每一条样本包含28个空域复杂度因子(由文献[12]总结，如表2所示)的取值，对应某一个扇区在某一分钟内的运行态势。

表2 空域复杂度因子列表Table 2 Set of spatial complexity factors

续表

为验证所提出的扇区复杂度无监督评估方法的准确性，邀请了管制专家对4个扇区样本的复杂度等级进行标定，包括“低复杂度”、“中复杂度”和“高复杂度”3种。

2.2 KPCA降维结果

针对每一个扇区，对其960条复杂度样本采用KPCA方法进行主成分提取(降维)。所用高斯核函数的带通参数设置为

(3)

式中：xi、xj为样本集中两条样本；n为样本集大小。表3展示了对应各个扇区样本集的主成分的贡献率(从大到小排序，仅展示前10个)。可见，对任意扇区，前两个主成分贡献率之和均超过88%，因此仅抽取前两个主成分(m=2)即能够保留原始样本蕴含的绝大部分复杂度评估知识。

表3 从各扇区样本所提取主成分的贡献率Table 3 Contribution rates of principal components extracted from each sector’s samples

2.3 基于主成分聚类的复杂度等级划分结果

按照4个扇区样本集被管制专家标定的情况设置聚类参数。聚类输出的结果如图2所示，横轴为样本被聚类算法判定的复杂度等级(“L/M/H”分别对应“低/中/高复杂度”)，纵轴为样本被管制专家评判的等级，圆面积正比于样本数量。可见，在4个扇区样本集上实验的结果显示，无监督模型在4个扇区样本集上平均评估准确率高达74%。实验结果说明所提出模型具有较好的扇区复杂度无监督评估性能，能够为空域划分、流量管理等实际空管业务提供有效的技术支撑。

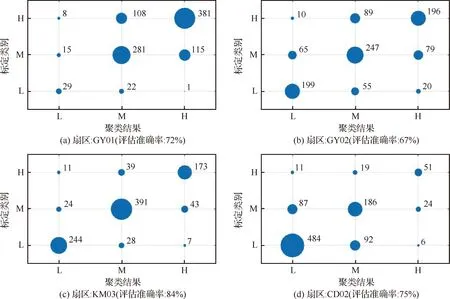
图2 扇区复杂度无监督评估结果Fig.2 Results of unsupervised evaluation for sector complexity

3 结 论

1)提出了一种基于核主成分分析的空域复杂度无监督评估方法，在不依赖标定样本的基础上通过主成分提取与主成分聚类对指定空域的复杂度等级进行划分，解决了由标定样本采集困难所导致的空域复杂度难以准确评估的问题。

2)采用的核主成分分析方法能够从多维因素中提取最大化空域复杂度评估知识的主成分；所设计的主成分聚类方法能够根据实际空域运行特点进行配置，满足模型用户对于不同扇区复杂度评估的具体要求。

3)基于西南区域4个扇区实际运行数据的实验结果表明，本方法能够在无监督条件下实现对扇区复杂度等级的准确划分。