基于静态博弈最后一公里配送时间的博弈

王靖，韩志斌

（长安大学 汽车学院，陕西 西安 710064）

引言

在很多中小型城市，最后一公里配送过程中，都存在一个非常普遍的现象：消费者正好在快递员去送货的这个时间段内从事别的活动，无法接收到商品，这将会导致快递员会重新进行一次配送，使配送时间延长以及使快递公司的配送成本提高，给企业带来经济利益的损失。而消费者也无法在期望的时间段内得到所需商品，给消费者也将带来一定的损失。针对这种现象，一些快递公司会通过数据挖掘等一些数据处理技术，会对消费者进行分类；有一部分顾客是：在快递员配送的时间段内，多次没有接受到商品，在本文中称此类消费者为特殊消费者。针对这类顾客，快递公司有两种策略：一是跟平时一样，只进行普通的预约；二是快递员会进行一次特殊的预约，跟消费者进行交谈，确定在哪天哪个时间段有时间。

本文将用静态博弈的理论构建特殊消费者C 和快递公司A 或B 之间针对最后一公里配送问题的模型，得出纳什均衡解。在特殊消费者不知道快递公司对此类问题解决的成熟度如何的情况下，选择对快递公司进行调查或不调查，然后构建不完全信息的静态博弈，得出贝叶斯均衡解。

1 理论基础

博弈论又称为对策论，“完全信息”是指每个参与者对其他参与人有完全的了解；“静态”是指所有参与人同时选择，而且只能行动一次。完全信息的静态博弈是最简单的一种博弈模型。分析的目的是预测博弈的均衡结果。如果所有参与者至少有一个不了解其他参与者的效用函数，且所有参与者同时参与采取行动，则该博弈为“不完全信息静态博弈”，又称“静态贝叶斯博弈”。

2 特殊消费者与快递公司之间博弈模型的建立过程

2.1 完全信息下的模型构建

基于最后一公里配送时间的问题，特殊消费者在选择快递公司的问题上作以下假设。

假设一：快递公司和消费者的行动时间一致。

假设二：特殊消费者C：在选择快递公司时，有两种策略：一种是选择相信某一家快递公司，直接选择，另外一种选择是采取一些措施进行调查。设特殊消费进行调查投入的成本为D1。

假设三：快递公司也有两类，一类是对这种特殊消费者群体进行特殊预约比较成熟的一种快递公司A；它可以保证消费者在期望的时间内得到商品，设其投入成本为E1；另一类快递公司则是刚起步快递公司B，对这种业务还不是很成熟，这类快递公司进行特殊预约的投入成本要高于第一类的投入，为F1,且F1＞E1。

假设四：快递公司B 对特殊消费者进行普通预约都是不成功的，即消费者不对其进行调查，则获得业务，若果对其进行调查，则会知道该公司能力不足，放弃选择该企业。

假设五：当消费者选定某种快递公司时，消费者在期望的时间内得到商品的价值量化为D2,没有在期望的时间内得到商品的损失为D3，D3＞D2，D3＞D1。

假设六：快递公司A 承接了消费者的业务，并能准确送大的收益为E2；快递公司B 承接了消费者的业务，并能准确送大的收益为F2；E2＞F2而E2＞E1，F2＞F1。

根据以上假设，针对最后一公里配送时间的问题，建立完全信息下的特殊消费者与快递公司A 和B 的支付-收益矩阵分别为如表1 和表2 所示。

表1 特殊消费者与快递公司A 的静态博弈

表2 特殊消费者与快递公司B 的静态博弈

2.2 完全信息下的模型分析

利用划线法，由表1 可以看出，无论消费者选择调查或者不调查，快递公司A 都是选择普通预约收益要高；对于快递公司进行特殊预约或者普通预约，消费者都是选择不调查收益最高，所以纳什均衡解为：（E2，D2），即特殊消费者选择不调查，快递公司进行普通预约时，双方受益最高。同理利用划线法，根据表2 的矩阵可以得出快递公司B 和特殊消费者的纳什均衡解是（-F1+F2，D2）。即特殊消费者在选择快递公司B 时，选择不调查，快递公司B 进行特殊预约时，双方效益最高。

2.3 不完全信息下的模型构建

实际生活中，特殊消费者在选择快递公司时，并不知道哪个快递公司实力强，会选择调查还是不调查，而快递公司也不知道特殊消费者会不会调查。也就是博弈双方存在不对称信息，即不完全信息的静态博弈。因此，增加以下假设：

假设七：特殊消费者不能准确判断哪家快递公司实力强，选择快递公司A 的概率为P1，则选择快递公司B 的概率为1-P1；特殊消费者知道快递公司进行特殊预约的概率为P2,则进行普通预约的概率为1-P2。

假设八：快递公司不知道特殊消费者会进行哪种选择，但知道其进行调查的概率为P3，不调查的概率为1-P3。

根据以上假设，基于不完全信息下特殊消费者和快递公司A 和B 的支付-收益矩阵如表3 所示。

表3 快递公司A 和B 与特殊消费者的静态博弈

2.4 不完全信息下的模型分析

根据表3 可以得出两个局中人的收益函数，然后进行具体的分析。

从快递公司A 的角度出发，它进行特殊预约的期望收益为：

因为E2＞-E1+E2，快递公司A 的最优策略是进行普遍预约。

快递公司B 进行特殊预约的期望收益为：

快递公司B 进行普通预约的期望收益为：

如果G1＞G2，即F2-F1+F2P3＞0，整理得：F2＞F1/（1+P3），则此时快递公司选择特殊预约，否则选择普通预约。

所以，快递公司B 是否选择特殊预约取决于快递公司B的成本收入F1和收益F2，以及特殊消费者调查的概率为P3。

特殊消费者进行调查时的期望收益为：特殊消费者不进行调查时的期望收益为：

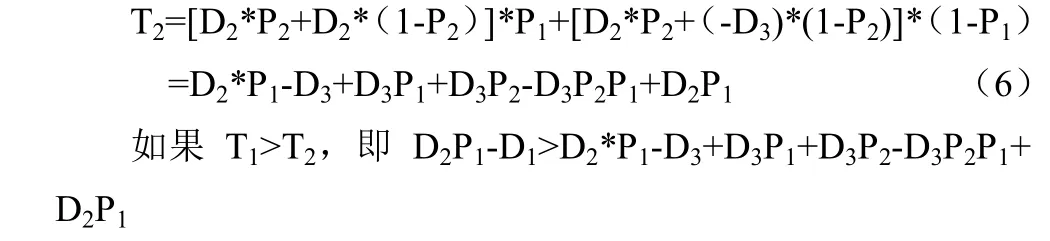
即D2＜[D3(1-P1)+D1]/P2+P3(P1-1),此时特殊消费者就会对企业进行调查，否则就不调查。由此可知特殊消费者是否进行调查取决于其调查投入的成本为D1、价值成本为D2、商品的损失为D3、选择快递公司A 的概率为P1和快递公司进行特殊预约的概率为P2。

3 结论与建议

物流领域最后一公里配送时间在现实生活存在多种不同的问题，本文就最后一公里配送是否能及时送达到消费者手中的问题进行建模，进行了一些假设，得出了纳什均衡和贝叶斯均衡解。

在完全信息的静态博弈模型下，即特殊消费者和快递公司双方之间都有完全了解的情况下，对业务比较成熟的的A类快递公司进行普通预约，特殊消费者不进行调查时，双方的收益得到最优解，即纳什均衡解为：（E2,D2），特殊消费者可以收益D2，快递公司A 的收益E2。对业务不太成熟的的B类快递公司进行特殊预约，特殊消费者不进行调查时，双方的收益得到最优解，纳什均衡解为：（-F1+F2,D2），特殊消费者可以收益D2，快递公司B 的收益为F2-F1，即B 公司的收益减去其成本。

在不完全信息的静态博弈模型下，即特殊消费者和快递公司双方之间都不知道对方的情况下进行选择，通过对收益函数的比较，且因为 E2＞-E1+E2，快递公司A 的最优策略是进行普遍预约。对于快递公司B 来说，当F2＞F1/（1+P3）时，则此时快递公司选择特殊预约是收益比较高，否则选择普通预约。从特殊消费者的角度来说，D2＜[D3(1-P1)+D1]/P2+P3（P1-1）时，此时特殊消费者就会对企业进行调查，否则就不调查。这里涉及的参数比较多，在现实生活中，需要对这些参数进行一个合理的统计分析计算加以确定，然后根据是否满足以下式子：D2＜[D3(1-P1)+D1]/P2+P3(P1-1)来决定是否进行调查。