基于围道矩阵的遗传算法求解柔性作业车间调度问题研究

崔晨浩 任工昌

摘  要：在经济全球化的时代，我国制造业面临着巨大的商机和激烈的市场竞争，企业在满足客户个性化需求的同时需要具备快速响应市场的能力，所以研究柔性作业车间调度问题（FJSP）成为解决这些问题的一个重要方向。在这样的背景下，本文提出一种利用多色集合理论中的围道矩阵，改进传统遗传算法，对FJSP问题中完工时间这一指标进行优化。

关键词：遗传算法;围道矩阵;完工时间;车间调度

中图分类号：TH164;TP18      文献标识码：A 文章编号：2096-4706（2019）24-0153-05

Abstract：In the era of economic globalization，China’s manufacturing industry is facing huge business opportunities and fierce market competition. Enterprises need to have the ability to respond to the market quickly while meeting the personalized needs of customers，so the study of flexible job shop scheduling （FJSP） has become an important direction to solve these problems. Under this background，this paper proposes a new method to optimize the completion time of FJSP by using the contour matrix of polychromatic set theory and improving the traditional genetic algorithm.

Keywords：genetic algorithm;enclosure matrix;completion time;workshop scheduling

0  引  言

制造业是社会经济的重要支柱之一。当下，中国制造企业的工艺过程与调度较多地依赖于人工经验，由于目前大多数制造企业的工艺过程与调度不够先进，制定的调度方案难以使得生产线资源利用最大化，最终影响产品的完工时间[1]。本文主要研究一类基于多色集合理论的工艺过程与调度集成的优化建模方法，以优化产品完工时间为目标，以此解决柔性作业车间调度问题。旨在降低生产成本，提高生产效率，从而提高企业的竞争力。

1  多色集合中的围道矩阵

1.1  多色集合理论

多色集合理论是一种新型的信息处理工具和系统理论，它的核心思想是使用形式相同的数学模型来仿真不同的对象（产品、设计过程、工艺过程和生产系统等等），来描述元素之间的层次结构与复杂关系，重点是在集合层和逻辑层组织与处理信息，再在数量层解决低层数量大小及数学计算问题。因此，多色集合理论在问题的形式化研究方向具有明显的优势，被广泛应用于产品的概念设计建模、零件制造工艺建模、产品装配工艺建模和工作流过程建模等领域[2，3]。

1.2  围道布尔矩阵

在对产品、设计过程和制造工艺过程进行建模时，集合论的数学工具得到了广泛的应用。但传统的集合论不能描述集合本身以及其元素之间的性质，这就限制了其在复杂系统建模方面的应用。使用多色集合来表示性质统一的标准数学模型来进行系统仿真，由于其中系统形式不取决于仿真对象的内容，从而使仿真系统更具柔性，也便于编程。基于此，该方向已成为关于多色集合理论的主流研究方向，多色集合理论使用了“围道”这一概念来代替纯数学理论中“颜色”的概念，以便更好地抽象与概括实际系统中对象的性质、属性、特征与参数等概念[4]。

2  柔性作业车间的调度问题及其约束

2.1  柔性作业车间调度问题

柔性作业车间调度是指生产车间中在m台设备上加工n个工件，每个工件包含ni个事先确定加工顺序的工序，每道工序可以在多台设备上加工，每道工序不同的机器加工时间有所不同，本文主要考虑完工时间最短的性能指标[5]。

2.2  车间调度的应用算例及约束条件

本文采用3×6×8的FJSP调度问题算例（3类工件，对应最大工序数为6，在8台设备上进行加工）來实现求解完工时间最小这一个目标。加工信息如表1所示。

2.4  约束条件

当工件i的第j道工序和工件e的第g道工序在同一台机床上加工时，设：

当工件e的第g道工序在机床k上加工时，设：

共有s个加工顺序，要求工件从开始加工到加工完成时间最短的加工顺序，那么要先求某一个加工顺序x，对应的工件从开始到结束加工的时间，也就是求x中所有工件的总完工时间，所以Ep=MS。

3  遗传算法操作步骤

3.1  加工信息处理

3.1.1  染色体单层编码

在进行染色体的具体编码之前，先进行码位信息的确定，第一种是显性码位信息，第二种是隐性码位信息，是显性码位信息的具体化即具体化某种工件的工序码位。

（1）确定染色体长度。染色体的长度为所有工件的全部工序数的总和。多件多品种生产方式：有N种工件共S件，第i种工件有Pi道工序。由于是多件多品种，首先得对数量大于1的多种工件进行加工顺序排布，写出显性码位信息，然后具体化每种工件的隐性码位信息即该种工件的具体工序编码。例：有A、B、C三种工件各1、2、3件。

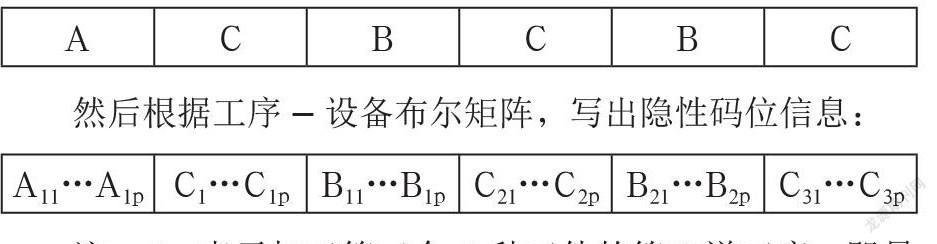
那么这6件工件的加工顺序有很多种，任意选择一种，写出显性码位信息：

然后根据工序-设备布尔矩阵，写出隐性码位信息：

采用围道布尔矩阵进行显性、隐性码位信息确定，不仅降低了编码的空间复杂度（原来需要二层编码），而且在解决批量生产问题时，只需要将工件种类作为显性码位信息，某种工件的工序加工信息作为隐性码位信息出现在矩阵中，再根据染色体的设备编码就能较为快速地求解调度问题。

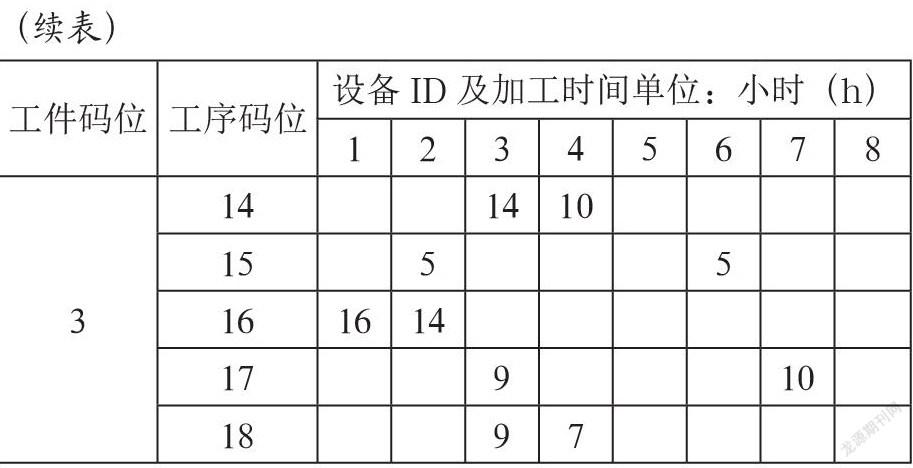
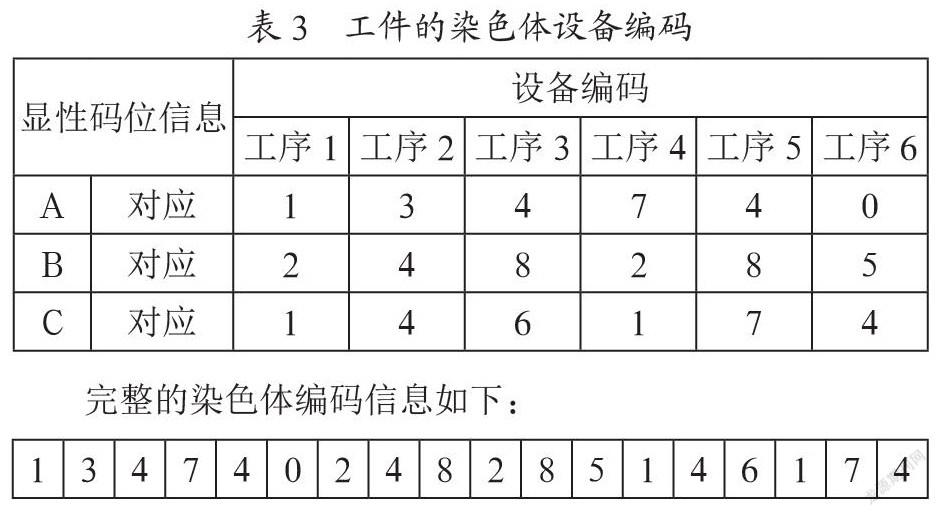
（2）确定染色体编码。根据A、B、C三种工件各1件的隐性码位信息，可以搜索对应工件的工序-设备围道布尔矩阵中，搜寻与工件的工序对应的可使用的设备信息，产生染色体，即产生每个工件每道工序的可用设备编码。如表3所示只是其中一种编码方式。

3.1.2  染色体解码

根据染色体编码，反向搜索工序-设备围道矩阵，从而获得各工序在相应设备上的加工时间。并在满足各工件工序约束的基础上，按照染色体（设备编码）对应的工序，在每台设备上安排的相应工序进行加工。

具体过程如下：将每台设备上各工件的第一道工序先进行加工，并返回工序-机床围道矩阵，获取其对应加工时间。（设备上的开始时间+工序加工时间=设备上最早完工时间=对应工件的某道工序的最早完工时间）按照工序约束与设备约束的双重约束，依次确定各设备上各任务的开始和完工时间;当确定出每台设备上所有任务的开始和完工时间，即可获得所有任务的加工方案，也就完成了解码过程。

3.2  适应度值计算

在遗传算法中，一个个体能否被遗传到下一代群体中，评判标准是该个体的适应度值的大小，适应度值越大，被遗传到下一代的概率越高。

设：fk=Ep=MS，适应度函数fit（k）=1/fk，k：表示第k条显性染色体

计算各设备上各工序的起始加工时间，完工时间。设工序j（j=1，…，P）的起始加工时间为Sj，完工时间为Ej，在设备k上的加工时间为Tj，那么有Ej=Sj+Tj（Tj已知，Sj未知）。

根据工序j的编号，搜索对应工件的工序-设备围道布尔矩阵，确定它是第几道工序。如果j不是该工件的第一道工序，那么搜索矩阵，确定j的上一道工序j0，得到j0的完工时间PreEj0，那么Sj≥PreEj0;如果j是第一道工序，那么Sj≥0。

根据工序j的编号，确定该工序在哪种设备上加工（如在设备k上加工），并确定该种设备的上道工序的编号。如果工序j是机床k上的第一道工序，k的起始加工时间为MSk，那么Sj≥MSk;如果工序j不是机床k上的第一道工序，k的上道工序的完工时间PreEk，那么Sj≥PreEk。

综述Sj取值，Sj=max（上道工序j0的完工时间，工序j在设备上的起始时间）。

3.3  选择、交叉、变异操作及结果

（1）选择。采用精英保留策略，根据适应度值fit（k）的 结果，将值最大的fit（k）对应的隐性染色体不经过后续的交叉变异，直接选择进入下一代的种群，保证优良性状的传承。

（2）交叉。根据交叉概率PC，随机选择两个染色体，并根据设定的交叉算子交换染色体上的部分基因编码，形成两个新的子代个体，评估其适应度值，选出适应度值较高的子代个体，进行后续操作。

（3）变异。选择一条隐性染色体，根据设置的变异概率PV，产生变异的码位，接着搜索工件的工序-设备围道矩阵，搜寻对应码位的可以代替的设备编码，从而产生新的个体。通过计算已经变异个体的适应度值fit（k′）和fit（k），若fit（k′）≥fit（k）则变异可行，反之变异失败，该条染色体无须进行变异。

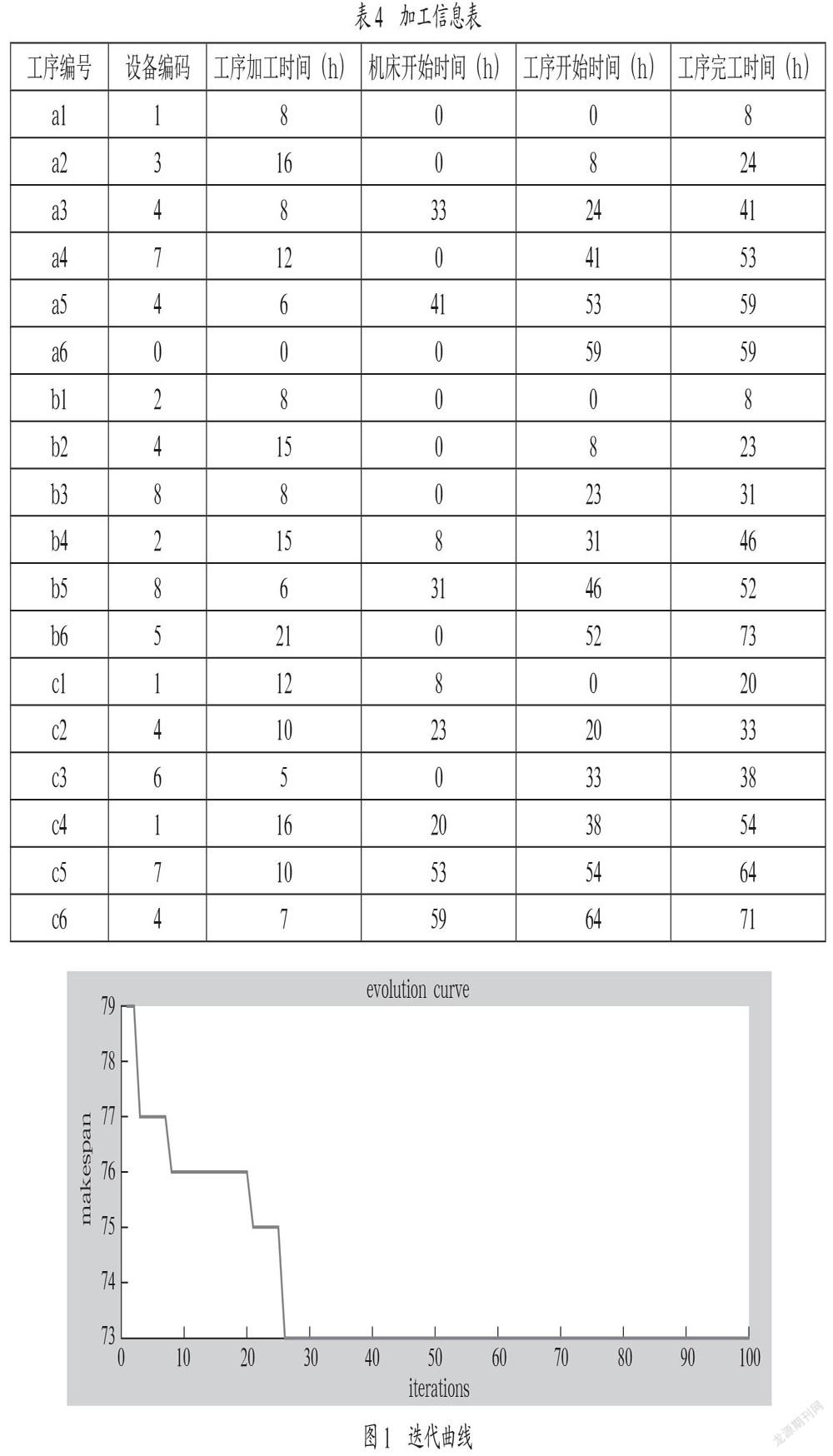
（4）结果。由于计算结果较为复杂，在Matlab中求解后得出加工信息表如表4所示、迭代曲线如图1所示。

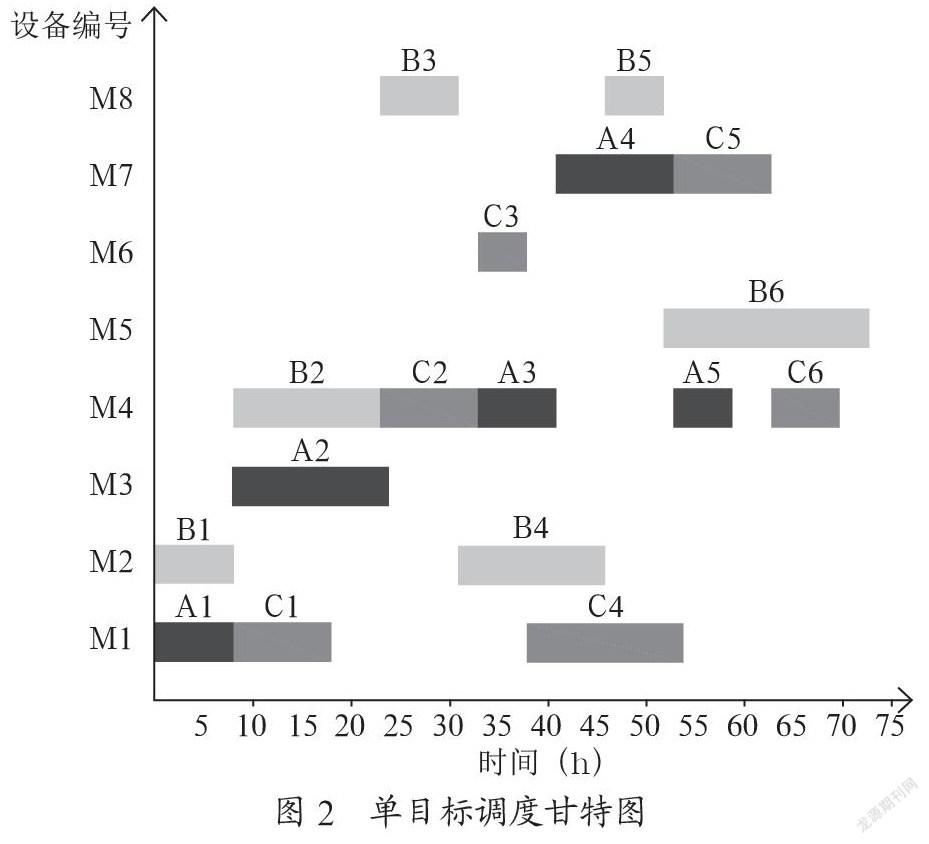
从迭代曲线可以看出，最小完工时间在迭代26次后趋于平稳，是73h，即为单目标调度的最优时间，并可以依据求解得出的加工信息表画出调度甘特图。如图2所示。

4  结  论

本文针对当下制造业中的单目标柔性作业车间调度问题进行了研究，构建了基于多色集合围道矩阵的改进遗传算法来解决改善作业车间完工时间的问题。改进遗传算法，是在多色集合的集成模型与数量排列模型的基础上，建立了柔性作业车间调度优化组合约束模型。采用此组合约束模型来处理调度中的工艺约束、设备约束和时间约束等，实现解域的构造与维护，再结合遗传算法来优化搜索解域。因此，改进后的遗传算法不仅保证了解的有效性，還显著提高了算法的求解速度。

参考文献：

[1] 张文生.改进的遗传算法在多目标车间调度中的应用研究 [D].大连：大连交通大学，2010.

[2] 张博，李宗斌.采用多色集合理论的公差信息建模与推理技术 [J].机械工程学报，2005（10）：111-116.

[3] Pavlov VV.Polychromatic sets theory of systems：Structure of PS [J].Information technology，1997（7）：11-16.

[4] 张国辉，高亮，李培根，等.改进遗传算法求解柔性作业车间调度问题 [J].机械工程学报，2009，45（7）：145-151.

[5] 张超勇，刘琼，邱浩波，等.考虑加工成本和时间的柔性作业车间调度问题研究 [J].机械科学与技术，2009（8）：1005-1011.

作者简介：崔晨浩（1993-），男，汉族，河南郑州人，硕士，研究方向：为制造系统资源调度的优化;任工昌（1962-），男，汉族，陕西西安人，教授，博士生导师，研究方向：产品创新理论、机电设备状态监控。