定理教学做好细节才会好

储成俊

摘要：本文通过对一节定理教学案例片断的评析，提出要做好定理教学细节，做到以问题贯穿教学全程，引领学生思维前行，鼓励学生自主学习，激励学生自己去发现。

关键词：定理教学  教学细节  自主学习

引言

初中定理教学是几何教学的重要内容，如何上好定理教学课一直是数学教师重点研究的课题。2018年下半年，滁州市开展以“初中定理教学”为主题的研讨活动，执教老师上了一节定理教学课，内容是沪科版数学八年级上“线段的垂直平分线”。笔者想就这节课的教学谈一点看法，对定理教学细节谈一点认识。

一、案例片断评析

1.引入新知环节片断

师：上节课我们学习了线段的垂直平分线，什么叫线段的垂直平分线？

学生回答。

师：这条直线有什么性质呢？这节课我们就来探究其性质。

【评析】复习导入法是常用的引入新课的方法，通过复习旧知来引出新知，层次鲜明，容易激发学生的学习欲望，旧知也得以巩固。执教老师仅让学生口述一下概念，这种复习停留在表面，收到的复习效果有限。如果让学生先画图，再结合图形复习，文形结合，以文释形，以形助文，这样才会收到较好的效果。在学生回答出概念后，执教老师直接设问，点出要探究的主题，稍显突兀。如果让学生分析概念所蕴含的性质，再追问有没有其他性质，学生会想到去探究，探究的主题是什么就不言自明了。

2.数学实验环节片断

师：古代弓箭在射击时箭应如何放置？

生1：箭放在弓的中点处。

生2：箭放在弦的中点处。

师：此时箭垂直平分弓吗？

生：箭垂直平分弓。

师：箭末端到弓两端的橡皮筋长度有何关系？若继续拉，上述关系还成立吗？

生：长度相等。继续拉的话，关系成立。

师：你是怎么得到的？

生1：用尺子测量长度。

生2：用绳子或线度量。

师：若箭不垂直或不平分弓，这个关系还成立吗？

生：不成立。

【评析】恰当地运用数学实验引导学生参与实践，有利于学生发现问题，培养探究性学习品质，树立主体意识，促进全面发展。执教老师巧妙地设计问题，明晰学生思维，引领探究方向，让学生在设问中思考，在释问中收获。

有待商榷的地方：（1）弓是弯的，用弓代表线段合适吗？（2）射箭时，箭是否一定放在弦的中点处？（3）弦容易形变，能比较箭两边弦的大小吗？（4）最后一问答案错了，因为经过一点的直线有无数条，即使答案没错，这个问题能起到什么作用？由此可见，情境要合适准确，问题要针对实效。

3.探究猜想环节片断

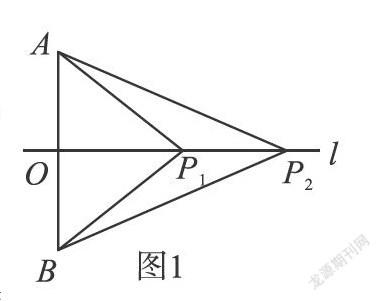
师：你能画出拉弓的两个状态图吗？你是怎么画的？

生：关键是画出线段AB的垂直平分线l。

師：图1中的P1A与P1B，P2A与P2B有何关系？

生：P1A=P1B，P2A=P2B

师：你是怎么比较的？

生1：用刻度尺测量长度或用圆规度量。

生2：沿直线l对折。

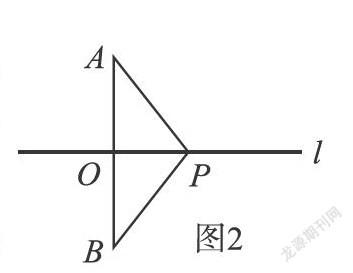
师：如图2，在l上任取一点P，则P到A、B的距离相等吗？

生：P到A、B的距离相等。

师：你的结论是在什么条件下得到的？

生：P在线段AB的垂直平分线上。

师：据此你有什么发现？

【评析】探究式教学是初中数学定理教学的常用模式。执教老师先让学生小组合作画图，感知直线l是线段的垂直平分线，体验P到A、B的距离相等。在体验的基础上，鼓励学生动手验证，归纳猜想。学生自己动手操作，探究才有乐趣，印象才会深刻。如果用几何画板演示P在l上不同位置的变化，这更有利于学生去观察验证。信息技术进入课堂，为学生探究打开了新天地。

4.定理证明环节片断

师：如何才能说明上述命题的正确性呢？

生：需要证明。

师：证明分哪几步？请你写出证明过程。

学生完成证明过程，教师评价。

【评析】证明一个真命题，一般要把文字命题转化为符号命题，概括为“一分二画三转”：分清题设、结论，画出对应图形，转化成符号语言。数学语言之间的转化，是几何学习的一个难点。执教老师在复习了命题证明的一般步骤后，立即让学生独立完成证明。从现场看，少数学生完成了证明，但大多数学生不知道怎么把文字命题转化为符号命题，可见教师未充分了解学情，放手太快。如果引导学生分析命题，正确画图，转化的困难将迎刃而解。

【总评】执教老师从弓箭情境出发，精心设计问题串，引领学生参与活动，激励学生探究交流，鼓励学生分享展示，引导学生去发现、去总结、去证明、去应用，充分调动学生参与的积极性，学生的数学素养得以发展。执教老师的教学理念新，教学效果好。但用弓箭类比垂直平分线值得商榷，教学细节的处理水平需要提升。

二、做好定理教学细节

1.创设合适的问题情境

问题情境要有数学味，体现数学特点，不能停留在形式层面，杜绝似乎有趣，而实际无用的情境。有针对性、启发性、挑战性的问题情境，才能激发学生思考，激励学生探索。最好从学生实际或数学背景中搜寻素材，创设接地气的问题情境，让学生经历新知的生成过程，这有利于学生探究和交流，发展良好思维品质。只有起点好，才会效果佳。

2.设计精致的问题串

问题是思维的开始，以问题串贯穿教学过程，引领学生在设问和释问中发展。问题串根据教学内容和学生实际设计，指向明确，解决什么问题，问几个问题，问什么问题，怎么问问题，都必须先设计好。这些问题往往前后关联，前一个是前提，后一个是延续，由易到难，搭建思维的阶梯，引领思维前行，经过抽象和提炼，不断逼近定理本质。问题设置要把握好坡度，太难会挫伤探究的激情，太简单会浇灭参与的热情。注重问的效果和问的水平，要在未知与已知、情境与目标之间架设桥梁，引领学生成长。

3.营造开放的探究过程

相信学生，充分放手，把主动权还给学生。以探究为主线，创设活泼的活动情境，并适时地引导和激励学生自己去观察、去实验、去思考，给学生猜想、归纳、总结的空间，真正做到让学生去合作、去发现。把教学过程营造成学生探究、解决问题的过程，使自主学习成为课堂主旋律，最大化地调动学生学习的主动性，让每个学生富有个性地成长，发掘内在潜能。

4.采用规范的命题证明

猜想需要证明，证明不仅能培养几何推理能力，还能培养严谨的探究品质。证明一般应先分清命题的题设和结论，画出对应的图形，写出已知、求证，最后探求证明方法，按照逻辑顺序写出证明过程。证明能帮助学生弄清定理的本质，加深对定理的理解。忽视对命题的分析，跳过命题几何化的过程，直接画好图，写好已知、求证，把教学重点放到寻求证明的方法上，这是对定理教学的一种伤害。把握每个细节，才能成就每一位学生。

5.进行有针对性的应用练习

定理是证明的基础、推理的依据，要让学生掌握定理，继而熟练应用定理。引导学生用三种数学语言分别表达定理，尤其是结合图形，用符号语言表达，更有利于学生直观地理解。定理的价值是应用，应用定理解决问题学生往往感觉困难，要设计有针对性的习题，指导学生去练习，让学生开始时就掌握定理的用法，提升應用水平。选择的习题一般先易后难，由浅入深。鼓励学生多思多练，在实战中掌握定理、总结方法、熟悉应用，避免以讲代练。还要设计一些变式练习，让学生熟悉各种应用情境。

6.打造自主的数学活动

数学课堂是数学活动的课堂，活动贯穿数学课堂始终，定理教学尤其如此。教学中依然存在轻过程重结果、轻自研重讲授、轻探究重应用的倾向，课堂如一潭死水，学习效率低下。学生充分自主，活动才有实效。教师要尝试改变，把课堂还给学生，把活动交给学生，运用信息技术和各种教具，帮助学生参与活动，鼓励学生动手操作、观察分析、归纳类比、猜想验证、推理论证、应用练习等。学生能解决的，教师绝不插手;学生难解决的，教师点拨引导。教师全程做好引领，调动学生的学习热情，挖掘学生的学习潜能。

结束语

初中数学定理教学做好细节为成，忽视细节为败。尽量以问题贯穿教学全程，引领学生思维前行，为学生自主学习搭建舞台，激励学生自己去发现，让自主学习成为课堂主旋律。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2] 教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读[M]. 北京：北京师范大学出版社，2012.

责任编辑：黄大灿