双倍比特量化近似查询索引算法研究

宋馥莉　闫培玲

摘 要：本文提出双倍比特量化与非对称距离的近似查询索引。首先，设计了一种双倍比特量化方法，通过把特征的每一维数据量化为两个比特二进制码，增加特征之间的区分性。然后，研究了非对称距离算法，通过计算浮点型查询特征与特征库中二进制码的距离，对海明空间下的最近邻进行重排序，以提高索引的查询精度。基准数据集上的实验表明，双倍比特量化与非对称距离的方法使最近邻查询精度提高15%～25%。

关键词：二进制量化;近似查询索引;双倍比特量化

中图分类号：TP391.41 文献标识码：A 文章编号：1003-5168（2019）25-0028-04

Research on Approximate Query Index Algorithms with

Double Bit Quantization

SONG Fuli1 YAN Peiling2

（1.Henan Radio & Television University，Zhengzhou Henan 450000;

2.Henan University of Chinese Medicine，Zhengzhou Henan 450046）

Abstract： In this paper， we proposed an approximate query index based on double bit quantization and asymmetric distance. First of all， a double bit quantization method was designed to increase the distinction between features by quantizing each one-dimensional data into two bit binary codes. Then， the asymmetric distance algorithm was studied. By calculating the distance between the floating-point query feature and the binary code in the feature library， the nearest neighbor in Hamming space was reordered to improve the query accuracy of the index. Experiments on the benchmark data set show that the accuracy of nearest neighbor query is improved by 15%～25% by using the method of double bit quantization and asymmetric distance.

Keywords： binary embedding;nearest neighbor search;double-bit quantization

1 研究背景

圖像检索[1]‎、计算机视觉‎[2]和目标检测[3]等领域的核心工作是高维特征的最近邻搜索。二进制码在进行图像检索方面有以下两方面优势：一方面，海明距离的计算非常高效，只需要几个机器指令即可完成[4];另一方面，二进制码占用的存储空间远远少于浮点型数据[5]。

本文设计了一种双倍比特量化方法，研究了非对称距离算法对海明空间的最近邻进行重排序，提出了双倍比特量化与非对称距离的近似查询索引方法，可以使索引的查询精度提高15%～25%。

2 研究现状

2.1 二进制量化

基于随机的映射和基于学习的映射是目前已提出的较著名的两类二进制映射技术，其中通用的是基于学习的映射。比如，主成分分析映射（Principal Component Analysis Embedding，PCAE）[6]通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分并作为原始特征的映射结果;谱哈希（Spectral Hashing，SH）[7]通过优化稀疏特征的权重差异来得到最优的二进制码，可将其看作是对PCAE每一维度都赋予不同权重的改进算法;迭代量化主成分分析嵌入（Principal Component Analysis Embedding Iterative Quantization，PCAE-ITQ）通过对数据进行旋转使编码和降维的误差最小化。

2.2 二进制索引技术

当前，高维索引领域的研究热点是基于二进制码的索引技术。局部敏感哈希方法在二进制特征的快速匹配上有一定效果。Rublee等人对ORB特征建立基于LSH的索引，Zitnick等人使用Min-hash技术对二进制特征建立索引。二进制特征之间的海明距离是度量距离，因此基于度量空间的索引可以应用于二进制特征的匹配。Muja等人提出建立多棵层次聚类树HCT来查询匹配二进制特征。HCT索引中采用256位的二进制码，并对特征库进行聚类。Norouzi等人[8]提出了多索引哈希技术（Multi-Index Hashing，MIH），对二进制特征的不相连子串建立多个哈希表，在海明空间下执行精确最近邻查找。

3 双倍比特量化与非对称距离

3.1 双倍比特量化

本文通过双倍比特量化把浮点型特征映射为二进制码的方法，提高了查询效率，并节省了存储空间，同时提出新的加权海明距离计算方法，提高了海明距离的计算效率。

为了准确地描述二进制映射技术的流程，笔者引入一组符号加以说明。[s]表示一个在Ω空间下的[K]维图像特征，[hk]表示一种二进制嵌入方法，即[hk：Ω→{0，1}]。由[K]个这样的二进制映射方法构成集合[H={hk，  k=1…K}]。二进制映射技术可以利用以下公式进行处理：

[hks=qkgks]                          （1）

其中，[gks：Ω→R]（R为中间空间）是投影函数;[qks：R→0，1]是量化函数。

为了解决传统量化方法只能粗略地把中间向量的每一维数据映射为两类（表示为0或者1），导致中间向量的区分能力大幅降低[9]的问题，本文提出利用加权海明距离来进行计算。

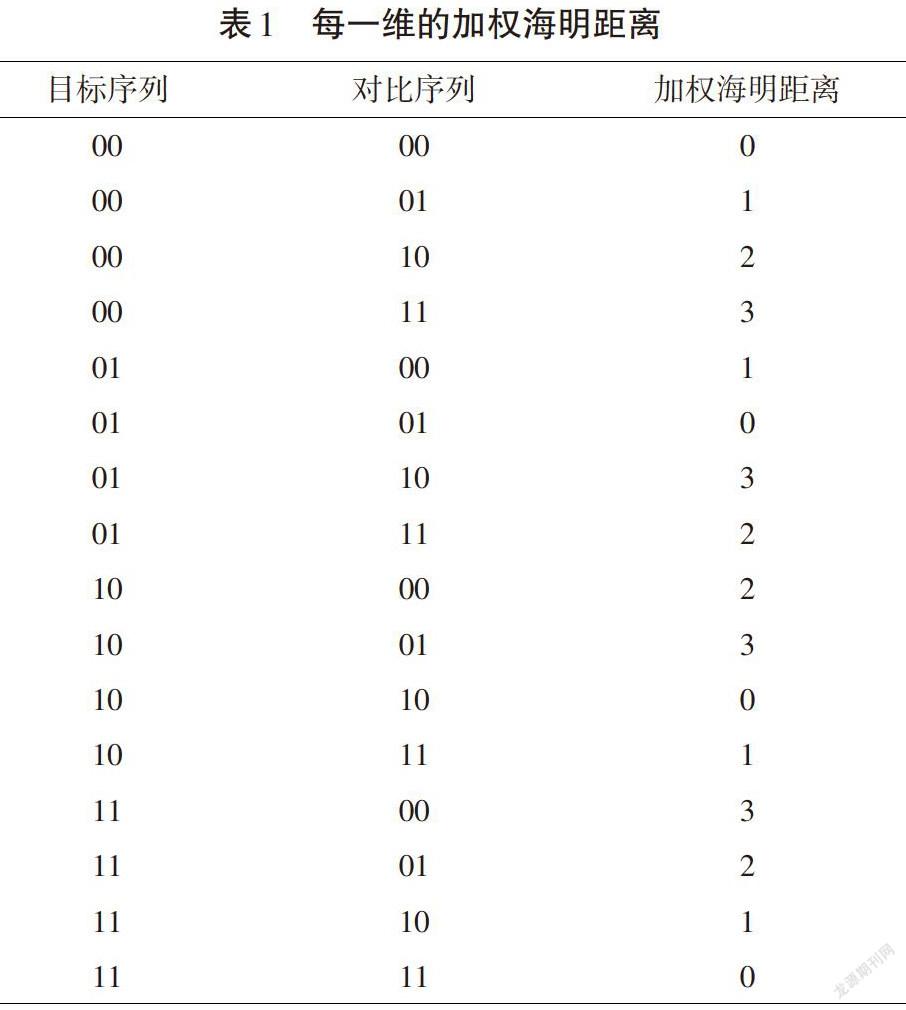
为了在线计算中间数据[r]与[q]之间的加权海明距离，笔者需要把每一维数据之间的距离相加。用[dkDBQkr，DBQkq]代表[r]与[q]第[k]维数据间的加权海明距离，具体表示如表1所示。

海明距离是指序列相同位置上数据不同的个数，而这里采用加权海明距离，即相同位置不同的数据表示为1，相同位置相同的数据表示为0，左一位对应的值乘以2的0次方，左二位对应的值为2的1次方，其距离为如表1所示。

根据海明距离的定义得到变量[r]与[q]间的海明距离：

[dWH（r，q）=kβr，qk]                           （2）

相比于查询特征与数据库中大量的特征之间距离计算，[β]计算的时间复杂度可以忽略不计。针对计算机内存对数据的存储是以字节为单位的，双倍比特二进制码之间的加权海明距离计算可通过对维度分组来进行。为了简洁地说明，本文假设k为4个倍数。所以，该计算方法可以表示：

[dWH（r，q）=k=0k/4-1j=1j=4βr，q4k+j]                      （3）

由于二进制子串[[DBQ4kr，  DBQ4k+1（r）]，[DBQ4k+2][r，DBQ4k+3r]]正好为1个字节，每个[j=1j=4βr，q4k+j]都只有256种可能的值。双倍比特量化方法可以使查询精度与查询速度都得到显著提高，如实验部分所述。

3.2 非對称距离计算

本文设计并实现了非对称距离算法，当获得一个查询特征后，笔者首先使用双倍比特量化的方法得到其在海明空间下的最近邻，并把这些最近邻作为候选集，最后使用非对称距离算法来对候选集进行重排序，以提高查询精度[10]。

大多数的二进制映射方法不仅要把特征库的特征转换为二进制码，同样也要把查询特征转化为二进制码。然而，笔者并不需要把查询特征也转换为二进制码，因为一个单独的未量化特征占用的空间可以忽略不计。非对称算法用于计算二进制码与未压缩的原始向量之间的距离，由于两种数据存在于不同的空间，所以我们把两者之间的距离称为非对称距离。非对称距离最大的好处就是它可以利用未压缩查询向量的优势以取得更好的查询精度。

由于双倍比特二进制特征之间的空间关系存在四种情况而非传统的两种，通过改进的非对称距离算法，特征之间的区分能力被进一步加强了。

4 实验结果及分析

4.1 实验设置

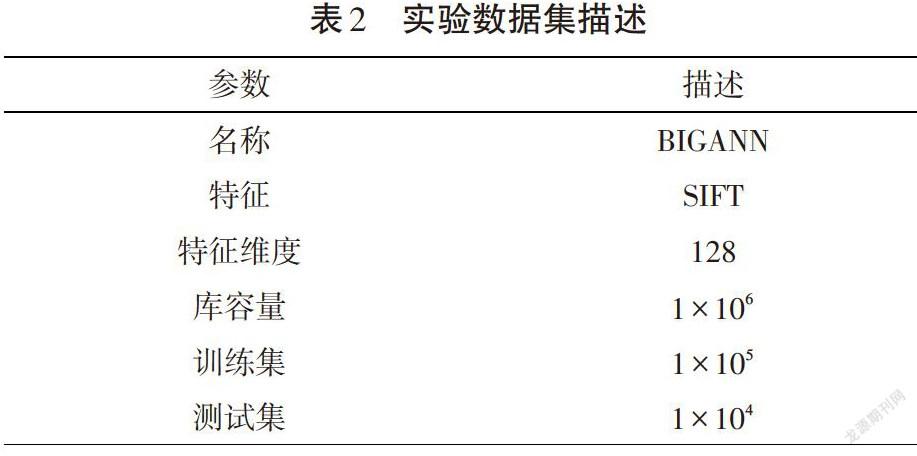
实验在BIGANN SIFT 1M数据集上开展，数据集描述如表2所示。其中，BIGANN数据集中的数据是高维特征：SIFT为128维，可供本文直接使用;而Caltech101数据为图像集。

在双倍比特量化的实验中，使用准确率与召回率来评估该方法的性能;非对称距离算法通过准确率进行验证。

4.2 双倍比特量化

每个实验包括了1 000个查询，这1 000个查询的平均准确率作为判断双倍比特量化的性能指标。实验在一个数据集中（BIGANN SIFT 1M）对比使用不同二进制映射方法。根据每个维度的正负符号获得中值，计算查询二进制码与每个二进制码的加权海明距离。

结果表明，双倍比特量化方法的查询精度总是高于传统二进映射算法，并且该效果与数据集、图像特征和二进制映射方法的选择无关。

4.3 非对称距离

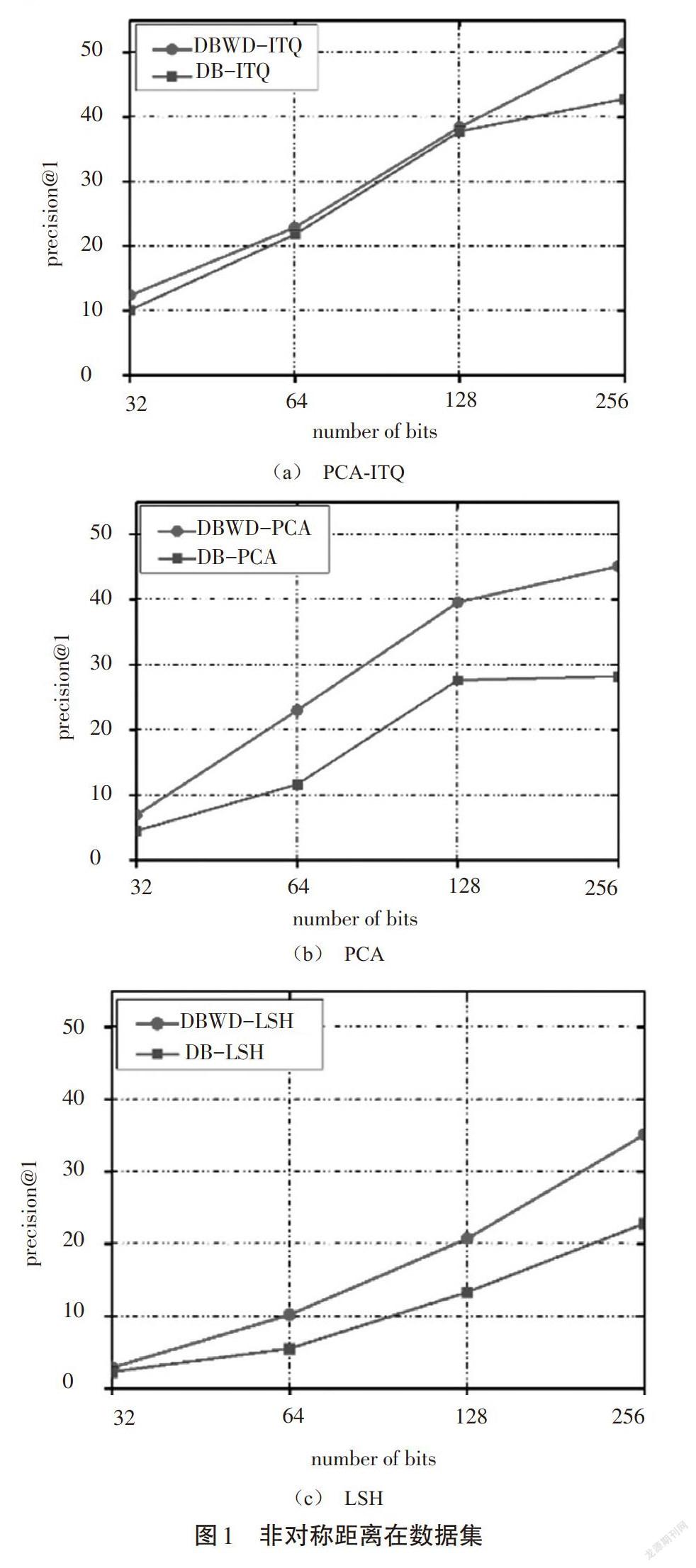
实验采用1 000个查询。由于笔者只对结果重新排序，召回率保持不变，所以该实验只使用准确率作为检测指标。数据集（BIGANN SIFT 1M）的二进制映射方法的实验效果中，使用非对称距离进行重排序的结果优于直接获得的结果。

图1表示在不同数据集中不同二进制映射方法使用非对称距离前后的准确率。即使双倍比特量化已经显著提高了精度，非对称距离仍进一步提高了最近邻查询准确率。在BIGANN SIFT1M和GIST特征数据集中，性能也很出色：如图1（b）所示，查询准确率平均提高了58.3%。

笔者注意到，当比特数较小时非对称距离的效果并不明显。由于二进制码是由双倍比特量化产生的，每两个比特仅表示一个维度。然而，非对称距离是由每个维度计算得到的。因此，当位数较小时，非对称距离的优势将受到限制。

5 结论

本文提出双倍比特量化与非对称距离的近似查询索引，把特征的每一维数据量化为两个比特二进制码以增加特征之间的区分性，计算浮点型查询特征与特征库中二进制码的距离，对海明空间下的最近邻进行重排序，提高索引的查询精度。在大规模数据集上的实验表明，本文提出的方法使最近邻查询精度提高15%～25%。

参考文献：

[1]贾佳，唐胜，谢洪涛，等.移动视觉搜索综述[J].计算机辅助设计与图形学学报，2017（6）：1007-1021.

[2]吴纯青，任沛阁，王小峰.基于语义的网络大数据组织与搜索[J].计算机学报，2015（1）：1-17.

[3]Lei Z， Zhang Y， Tang J， et al. Topology preserving hashing for similarity search[C]// Acm International Conference on Multimedia. 2013.

[4]Wang J， Shen H T， Song J， et al. Hashing for Similarity Search： A Survey[J]. Computer Science，2014（1408）：1-29.

[5]Yan C C ， Xie H ， Zhang B ， et al. Fast approximate matching of binary codes with distinctive bits[J]. Frontiers of Computer Science （print），2015（5）：741-750.

[6]Benzrihem N， Zelnikmanor L. Approximate nearest neighbor fields in video[J]. Computer Science，2015（8）：5233-5242.

[7]Weiss Y， Torralba A， Fergus R. Spectral hashing[C]//International Conference on Neural Information Processing Systems.2008.

[8]Norouzi M， Punjani A， Fleet D J. Fast Exact Search in Hamming Space With Multi-Index Hashing[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence，2013（6）：1107-1119.

[9]M. Raginsky，S. Lazebnik. Locality-Sensitive Binary Codes from Shift-Invariant Kernels[EB/OL].（2013-08-13）[2019-07-20]. http：//www.doc88.com/p-3922945380458.html.

[10]Gordo A， Perronnin F. Asymmetric distances for binary embeddings[C]//Computer Vision & Pattern Recognition.2011.