Study on Expected Mature Age of Individual Saliz matsudana

Lingling LI Keqin LI Jing ZHANG Dequan ZHANG Zhijun YANG Hongbo QIAO

Abstract Based on the study of parse wood materials， the fitting empirical equation of tree growth was obtained， a function with tree growth as a variable and time as an independent variable. Through mathematical operations such as function derivation， the mature age of tree growth was obtained， and the obtained expected mature age of Saliz matsudana was 21a. And the application， research directions and precautions of the mature ages were proposed.

Key words Mature age; Empirical equation; Parse wood

In forestry production， the formulation of cutting quotas and cutting area design must first meet the problem of the maturity age of trees. However， Shandong Forestry has done less work on the basics of the number table. Most of them use foreign or national standards， and remain unchanged for decades， which will inevitably cause great deviations. In this paper， by using the data of parse wood materials， the maturity ages of Saliz matsudana forest were studied. S. matsudana is one of the main tree species for gardening greening in Shandong Province. Its buds are edible， and the willow products are the initial materials used in the weaving industry， which play an important role in rural economic development and export earnings. S. matsudana is resistant to pruning and shaping， has a beautiful tree structure and a strong cultural heritage. Therefore， exploring the growth law of S. matsudana is of great practical significance for promoting socialist cultural construction and ecological civilization construction.

Data Sources

Due to limited funding， the previous survey materials were used in the paper. The parse wood materials were collected from a 11 year old S. matsudana tree with normal growth from Majiahe Forestry Farm， Guan County on April 3， 1984. The diameter at bread height （DBH） was measured in the section of 0.6 m， and other parameters were measured in the section of 1.0 m. Round circles were intercepted at the tree height of 5 cm （circle 0），  0.5 ， 1.3 ， 2.1， 3.1， 4.1， 5.1， 6.1， 7.1 and 7.6 m， and the circles were strictly interpreted in accordance with the technical requirements of parsing wood. Relevant information was collected with the age class of 1 year.

Research Methods

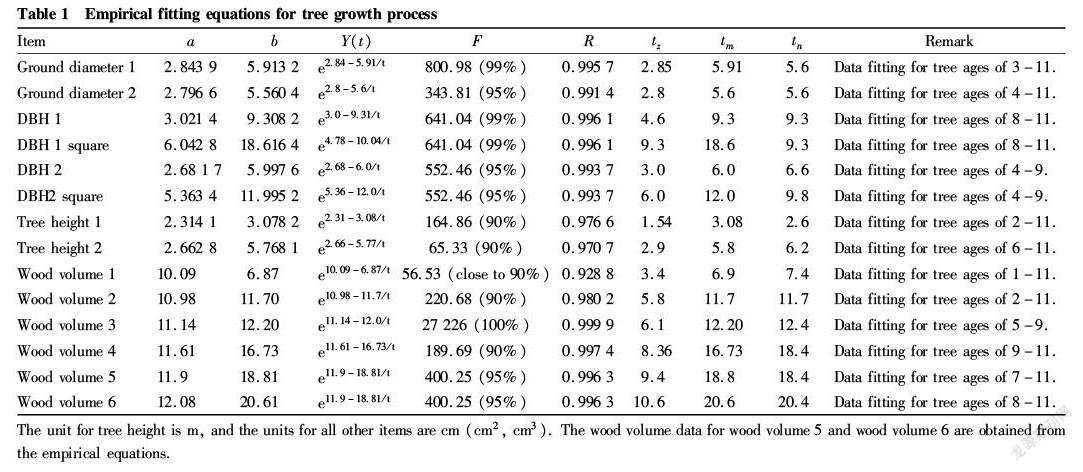
In order to save research costs， based on the analysis of parse wood data， fitting tests were conducted to various regression equations using previous research[1-3] by referring to previous research methods and processes[4-5] and research results[6]. Finally， the following mixed empirical equation was adopted to study the growth of the tree：

y（t） =e a-b/t

Where， a， b are the exponential parameters of the function to be solved; e is the base of natural logarithm 2.718 28...）.

The growth of trees is affected by various factors， but the growth of S. matsudana was greatly affected by the precipitation volume and uniformity of spatial and temporal distribution. Based on the empirical equations to fit the process of tree growth， the quantitative mature age of ground diameter growth was obtained by getting the maximum age from ground diameter fitting equation （including the equations generated by the derivatives， expressed in the research process）， the mature age of tree height growth was obtained by getting the maximum age from the tree height fitting  equation.  The same method was used to get the quantitative mature ages for the growth of DBH， DBH square， tree height， wood volume.

Research Process

A linear equation was obtained by taking the logarithm of the tree growth equations， which was then used to get the values of parameters a， b. The F test and correlation coefficient R test of the 2 parameters were performed[2]. Through the tests， the tree growth fitting equations were established （Table 1）. As shown in Table 1， the empirical equation of wood volume 1， which passed the F test with the reliability close to 90%， the fitting equations of tree height and wood volume 2， volume 4 all passed the F test with the reliability over 90%， and the fitting equations of DBH 2 and ground diameter 2 （and its square）， wood volume 5， wood volume 6 all passed the F test with the reliability over 95%. In addition to the above equations， all other passed the the F test and R test with the reliability over 99% （100% for the equation of wood volume 3）， indicating that this mathematical model （the empirical fitting equation） was applicable as a whole. All items passed the correlation coefficient R test with reliability of 99.9%， suggesting that the fitting equation relationship was established. The obtained maximum time of current annual increment and quantitative mature age of trees from the fitting equations were illustrated with the ground diameter as an example. For the equation of growth rate of ground diameter （current annual increment was completed by the derivation of the function Y（t） in Table 1， and only the extreme point was given in the paper）， the extreme point t z=2.85 a， that is， the current annual increment reached the peak when the tree reached 3 years old or so， and the peak was a single one. For the equation of average growth rate of trees  Y（t）/t  （annual average increment， and only the extreme point was given in the paper）， the extreme point t m=5.91 a， so the quantitative mature age of the tree was 5.91 a. In this paper， only the fitting equations for ground diameter were stated， and all other fitting equations were done in the same way. The meanings were all the same for growth fitting equation， tree growth rate equation， tree average growth speed equation， so were the meanings of symbols of t z， t m. Therefore， the calculation results were given directly in the paper. The quantitative mature ages of each item were shown in Table 1. As shown in Table 1， the parameter values were doubled compared with the values of the indicators and the squares of the indicators， but the accuracy was equal to the F test values and R test values. This was caused by the exponential mathematical relationship. This fitting equation for DBH square was established specifically to compare with the accumulation fitting equation. In Table 1， the values of t n were the ages at the intersection points of the curves of current annual increments and annual average increments of the sample wood （wood volume greater than 11 a was obtained from the tendency chart of growth curve）， which could be used as the actual mature ages of the tree. Only the t m values of ground diameter and its squared were far from the t n value （the parameters of ground diameter square were twice the ground diameter， but the test accuracy remained unchanged， which could refer to DBH）， and the t m values of the remaining  items  were very close to the t n values. The fitting values of the square fitting equations for ground diameter squares and DBH 2 were quite close to the fitting values of the equations for wood volume 2， wood volume 3， and the fitting values of the equation for DBH 1 square were very close to the fitting values of the equation for wood volume 5. Therefore， the empirical equation was more applicable for wood volume， and the results were more reliable. Concerning with the maturity of trees， the major factor was the maturity of wood volume， and thus， according to the research results and the needs for production practice， it was more suitable to set the mature age of accumulation volume as the mature age of the tree. The fitting results of wood volumes calculated from empirical equations were quite different from the data fitting results obtained from parse wood analysis， but the fitting accuracy was greatly improved， thereby indicating that the accuracy and applicability of the test were reliable.

Through comparative analysis， the mature ages of S. matsudana were set as 7 years， 12 years and 20 years respectively for the cultivation of woods as small sized timber， medium sized timber and large sized timber in combination with the production practice. For afforestation renewal after maturity， it is necessary to use seedlings or improved seedlings obtained from cutting seedlings from younger seedlings to prevent germplasm degradation due to shade regeneration.

Conclusion and Application

The mature ages were set as 7 years， 12 years， and 21 years， and the mature age of 21 years was based on the national age standard of 5 years， which was completely consistent with the original standard. The division of the age groups was shown in Table 2.

Discussion

The original standard mature age was 21a， which was made using a 5 year age class standard. On the other hand， in this study， the research conclusion was made using 1 year as the age class. For the convenience of production， the mature age is set at 21a， which was closer to the reality. In this study， it has found that there were 2 or even more growth peaks for the tree. In previous studies， such case was treated as growth aberration， and multiple tests （including other tree species） found that such cyclical variation of growth existed. The equation fitting results also showed such conclusion. However， as far as we are concerned， such case may be related to the fruiting year of the tree （the good year for seeds and fruit may be the lean year for wood volume， or vegetative growth）， and it may also be related with the inter annual periodical change of annual precipitation， both of which need to be studied separately. In this study， the mature age of trees is obtained through equation fitting based on the analysis and judgment of growth curve tendency when there is a lack of observation data of tree age class of 12 years and above. The study results show strong similarity and equation suitability with previous studies on Ouerus acutissima， Robinia pseudoacacia and Larix， so the obtained mature ages are applicable in future production practice. It is recommended that the further research achieve better results by using such method with the assistance of new techniques and equipment of medical imaging technology in tree measurement， so as to make the study more practical. The application of the empirical wood volume equation makes up for the lack of test data， which has achieved good effect. However， due to the various limitations， various deviations are inevitable， which can only be improved and developed in the future production research practice. The proposed forestry production suggestions only represent personal opinions. After all， the conclusion is obtained by analyzing the parse wood materials of an individual tree， and can only be applied after being approved by relevant experts and tested by production practice.

Agricultural Biotechnology2019

References

[1] LANG KJ. Forest measurement[M]. Northeast Forestry University， 1985： 283-296.

[2] CHEN HH. Mathematical statistics[M]. Beijing： China Forestry Publishing House， 1985： 205-251.

[3] LIU GJ. Registered consulting engineer （investment） qualification examination materials review guidance[M]. Tianjin， Tianjin University Press， 2003： 231-246.

[4] HU HY. Research on the actual maturity of individual Pinus densiflora[J]. Journal of Shandong Forestry Science and Technology， 2010， 6：  36-37.

[5] LI LP， DONG HF， ZHANG HB， et al. Study on anticipant mature age of Pinus densiflora in Shandong Province[J]. Journal of Anhui Agricultural Science， 2017， 3： 184-186..

[6] GAO JH. Approach into desirable period of forest management in Shandong Province[J]. China Forestry Science and Technology， 2003， 3： 6-8.