单元教学模式的尝试与思考

孙莉萍

开始备课时，我认为两种画法是两个独立的存在，对于学生为什么学习了度量法还要学习尺规作图，查阅了相关资料给出的解释是：在用量角器画已知角的过程中，我们在读数每位同学的近似方法不一样，实际上画出的角是会有误差的，这里有主观因素在其中。古希腊数学家最信任的尺规作图，所以我们作出一个角等于已知角。在备课组活动说课时，备课组老师建议用线段和角画法的类比学习会使知识脉络更清晰，更符合单元设计的要求，也就是现在复习引入中我们类比了画线段等于已知线段的方法后，让学生接着思考画一个角等于已知角的方法会有哪些来引出我们今天要研究的两种画法。

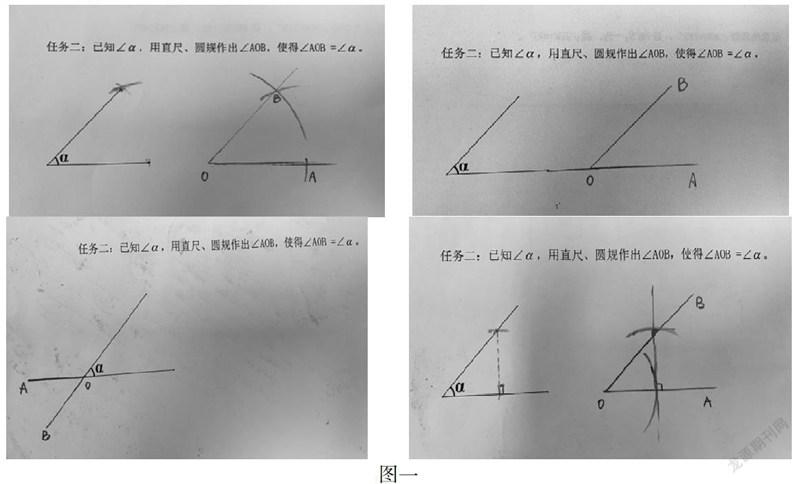
本课重难点就是探究尺规作图画相等的角的依据和过程，本以为探究只是公开课的一个形式，当时由于时间关系，准备给学生一分钟自己画，结果试讲时收到了“两边分别平行的角”、“对顶角”，“SAS”、“HL”甚至还有把圆规两个角当做角的两边，直接移动得到的（如图一）。通过这一环节也让我感受到六年级学生学习几何更多的凭借直观和直觉，他们需要通过猜想和动手操作去获得知识。

于是在备课中，我用几何画板让学生通过观察发现，猜想归纳。

在自主探究后，师生共同探究尺规作图的依据和过程，我一共做了三个尝试：

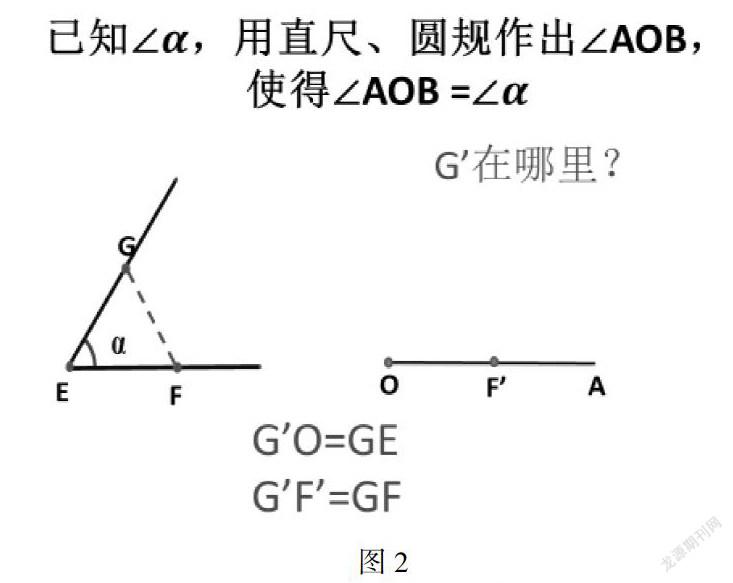
1.把画相等的角这个新问题转化为画相等的线段：GE、GF、EF，利用我们已学过的知识来解决未知问题，难点是如何确定G点。（如图二）

分析：①G点在以点E为圆心，长度为EG的这条弧线上;

②G点同时也在以点F为圆心，长度为FG的这条弧线上.

这两条弧线的交点就是E点.

这种方法作出的角一定和原来的角相等.它的原理我们在以后会学到，有兴趣的同学可以提前研究一下。这种方法作出的角一定和原来的角相等.它的原理我们在以后会学到，有兴趣的同学可以提前研究一下.但是要画三条长度不同的线段比较麻烦，我们在作图时可以取GE=EF，简化作图过程。老师在黑板上尺规作图，并口述作法。

这个说法看上去在讲道理，其实讲的道理学生较难理解。再反观学生的动手操作过程，他们更喜欢用直尺，而不知道圆规可以干嘛，角是有公共顶点的两条射线，那他们怎么会想到用圆规在角上画弧呢。备课组又经过讨论，觉得画弧就是角的始边上一个点绕着顶点旋转走过的路径，我反复旋转着发现这样就像量角器的半圆弧，想到用类比量角器画角。

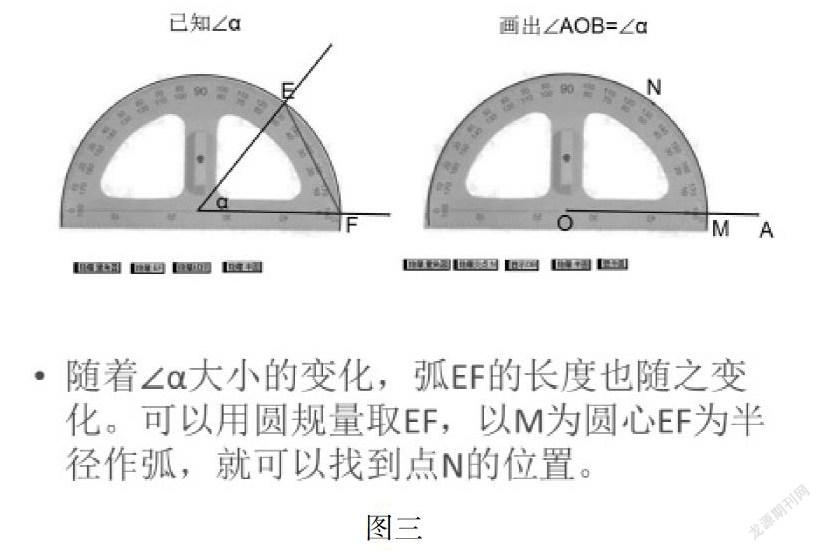
2.我们从角的动态概念来看，角是一条射线绕着它的端点旋转到另一个位置所成的图形。始边在零刻度数的点E绕着顶点旋转到终边上的刻度数点F，在旋转过程中，形成以顶点为圆心，GE为半径的弧，这个圆弧就像我们量角时第一次摆放的对中，对边的量角器。在画角的时候这条弧上的的刻度数处描出点N，就可以画出相等的角。那么在没有刻度的情况下，我们如何找到点N呢？学生通过几何画板动态演示，可以直观感受到随着∠α大小的变化，弧EF的长度也随之变化。可以用圆规量取EF，以M为圆心EF为半径作弧，就可以找到点N的位置。联结EF，可以通过EF的长度来确定角的大小，因此我们把画相等的角转化为画相等的线段。（如图三）

这个说法把量角器为什么是个半圆弧都解释清楚了，看似没有问题，可是从头到尾，就是老师一个在演示和讲，学生除了能感觉出EF的大小和角度有关系之外，没有感觉到量角器画和尺规画法的类比关系，会画的孩子不到1/3。

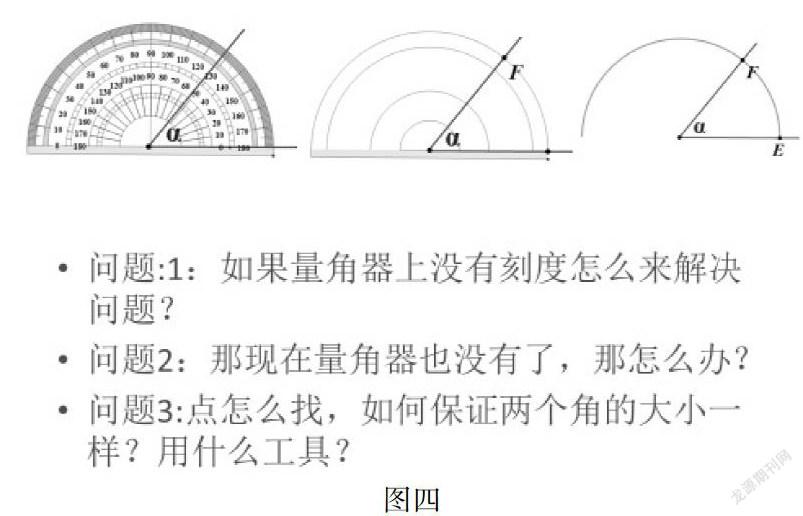
3.随着备课的深入，再次回到孩子的年龄特征和认知水平上来，把问题抛给孩子，而且需要层层递进，从“特殊”到“一般”。用量角器画角的时候在这条弧上的的刻度数处描出点N，就可以能确定OB的位置了。（如图四）

问题：1：如果量角器上没有刻度怎么来解决问题？

问题2：那现在量角器也没有了，那怎么办？

学生会马上想到没有刻度我就在弧上做个标记，弧也没有了我就造个弧，就能做标记了。

问题3：点怎么找，如何保证两个角的大小一样？用什么工具？

这时用几何画板让他们感受下EF之间的距离与∠α的大小有关，而截取EF就是之前的画线段的方法。因此我们用圆规作圆弧代替量角器，用圆规度量两点间的距离，保證了两个角的大小一样。

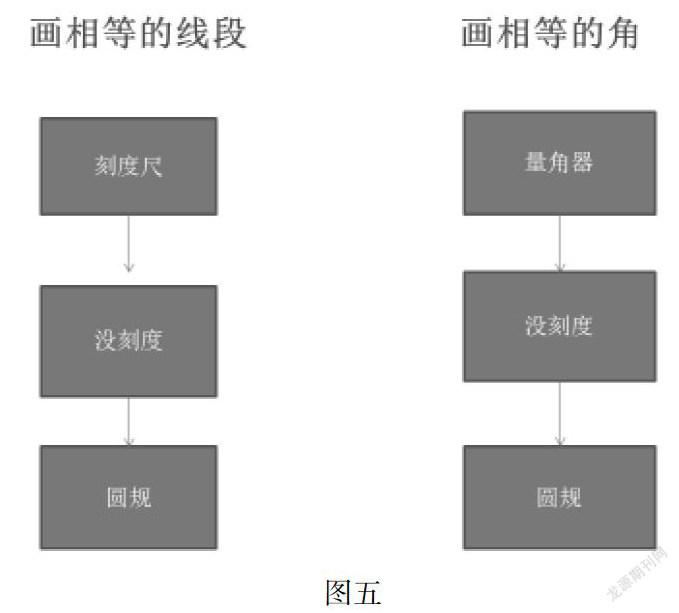
抛出这三个问题后，我突然又想到，画相等的线段的度量法和尺规画法不也可以这样讲吗？相等的线段怎么画？先画一条射线，再用刻度尺度量，然后在射线上截取。刻度尺没有刻度怎么办，在尺的一边上标点，再射线上找到另一个端点。那不用尺可以吗？我们可以用什么工具来代替找到端点呢？提出这样的问题，不是让学生在学习画图方法的过程中，也学会解决问题的方法了吗？（如图五）另外，在角的两种画法学习中，逐步使学生学会口头表达，不断规范几何语言，在练习中渗透分类讨论思想，也是为下一节角的和差倍做铺垫。

从刚开始备课认为2种画角的方法是割裂开的，在通过不断的磨课，不断反思中发现在这个单元教学的内容中，线段和角的各种类比，概念、大小比较、画法、和差倍分，甚至还能够把度量法与尺规作图做类比学习，有利于以后在设计时对这些碎片化的知识更系统整体的教学。还发现明确这个单元的教学目标，对于知识点怎么讲，讲到什么程度会更明确，有利于在每一阶段的学习更有层次性。

（作者单位：同济大学附属七一中学）