数据拟合方法在航空器航迹仿真中的应用
2019-09-10余娇


摘 要:通过航空器飞行的雷达原始数据可以绘制出航空器的飞行航迹。从雷达基站获取的原始雷达数据包含着繁杂的信息,本文首先对原始雷达数据进行了抽取和选择处理,对雷达数据中出现的赘余和缺失分别用不同的方法进行了修正。利用数据处理得到的雷达数据,本文应用数据拟合方法进行了航空器航迹仿真预测,绘制出了数据拟合后的航空器航迹图像,通过与原始数据图像进行对比,可以发现拟合方法在航空器航迹仿真中的优缺点。
关键词:空中交通管理;航迹仿真;数据拟合;
中图分类号:V557
1.引言
近年来,随着我国航空业快速发展,航班飞行流量不断攀升,空域内的管制工作越来越繁忙,管制员工作负荷也越来越高,空域资源短缺与飞行流量增长的矛盾凸显。通过对航空器实际飞行航迹的大量复现可得到航空器原始航迹的大数据,对航空器原始航迹的大数据研究可以为空域规划、进离场航线优化、扇区划分、流量控制等提供数据参考。航空器原始航迹的大数据来源于每一个航班的飞行航迹,利用航空器飞行的雷达原始数据可以绘制出航空器的飞行航迹,在处理原始雷达数据的基础上,应用数据拟合方法可以绘制出单一航空器的航迹,因此数据拟合方法在航空器航迹仿真中具有较强的使用性。
2.国外主要的航迹预测方法
目前应用于航迹预测研究中的算法主要有无参数估计法和基于航空器动力学的飞行模拟法。
基于卡尔曼滤波或者神经网络等的无参数估计方法是一种基于历史数据的航迹预测算法,不需要建立空气动力学模型。提出一种基于扩展卡尔曼滤波的航空器状态估计方法,通过当前航空器的状态和运动模型来对航空器航迹进行预测。基于混杂系统理论,谢丽利用交互式多模型算法对航迹进行预测。
基于航空器动力学模型的方法是利用航空器飞行过程中的各种性能参数对航迹进行预测的方法,此方法需要大量的飞行性能参数重点研究了下降进场的四维航迹控制技术与优化。王超提出了一种基于基本飞行模型的4D航迹预测方法,构建水平航迹、高度剖面和速度剖面,根据航迹特征点的飞行状态信息拟合生成完整的4D航迹。
3.航空器航迹数据处理
3.1 原始雷达数据的前期处理
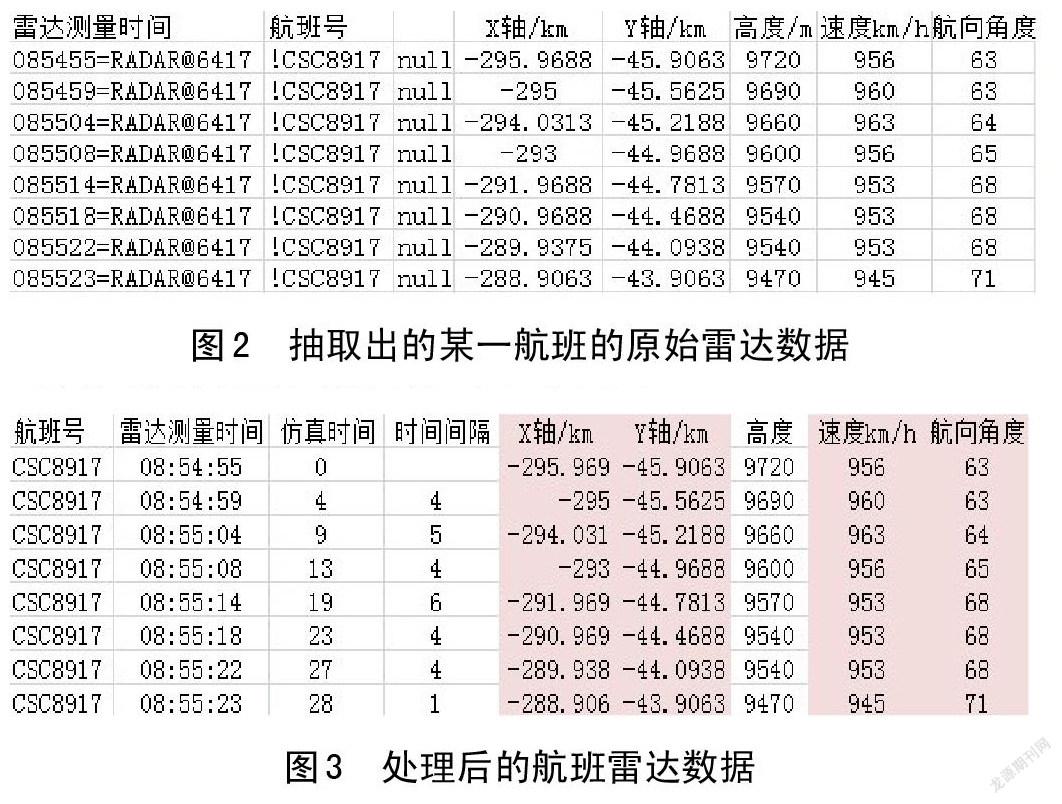
从雷达基站获取的原始雷达数据包含着繁杂的信息,这些数据并不能直接进行运用,雷达数据的处理是航迹仿真的前期准备,数据处理过程的正确与否也直接关系到后续航迹仿真结果的正确性。因此要对其中有用的数据信息进行提取,部分原始雷达数据如图3-1所示:
根据雷达基站提供的原始雷达数据,可以从中提取出相同航班号的所有雷达数据,然后根据雷达测量的系统时间显示的先后顺序进行排列,由此就可以得出该航班号的航空器在空间运行时的飞行状态变化过程。如图3-2所示:
3.2 雷达数据的抽取与选择
从原始雷达数据中提取出来某一航班的雷达数据后,还要对这些数据进行抽取和选择。首先要对雷达测量的系统显示时间表达形式进行修改,如将系统时间085455改为形如08:54:55的标准时间形式,在Excel表格中调用left、MID、right函数就可以实现时间表达形式的转换。将雷达第一次测量时间定义为仿真时间的初始时刻,即0时刻,用任意一次雷达测量的系统显示时间减去第一次雷达测量的系统显示时间就可以得出仿真时间,用任何两次相邻仿真时间相减就可得出系统仿真时间间隔。可以得出包含仿真时间和仿真时间间隔雷达数据表,如图3-3所示:
以上数据表中的雷达数据还存在很多不足,比如雷达数据的赘余和缺失,雷达数据的赘余或者缺失都会对原始航迹的精度造成影响,也会使后续仿真预测航迹产生偏差,因此要对赘余的雷达数据进行删除,对缺失的雷达数据进行填补。
运用MATLAB中的interp1线性插值函数,分别对航空器X轴位置、Y轴位置、航空器速度以及航向角度进行线性插值,对缺失时间段内所缺失的数值进行填补。用MATLAB做出速度的线性插值如图3-4所示:
按照如上方法再对Y轴数值、航向角度分别进行线性插值后填补的数值如下:
4.数据拟合的航空器航迹预测步骤
4.1 飞行参数处理方法
由所得的雷达数据可知,每一个仿真时间都会对该相应的航空器位置、速度和航向角度,随着仿真时刻的递推,航空器速度和航向角度在发生着变化,用数据拟合方法可以得出航空器速度和航向角度随着仿真时间变化的函数,得出拟合函数后就可以知道任意时刻的航空器速度和航向角度,由此可以将不规则的仿真时间间隔定义为统一的时间间隔,可以提高航空器航迹预测精度。
在不考虑航空器高度和上升下降的前提下,可以建立二维坐标系对航空器的航迹进行模拟,以机场归航台雷达基站为坐标中心,以地磁北极和与其垂直的东向分别为Y轴正向和X轴正向,航空器的位置可表示为在X轴和Y轴上投影的数值,建立坐标系后,可以将航空器的空间位置分解在X轴和Y轴上,由此可以建立如下的关于X轴和Y轴航迹方程:
由于航空器速度和航向角度的原始数据可知,但是速度和航向角度随着测量时间在不断的变化,要求出某一时刻航空器的速度和航向角必须要得就要得出速度和航向角随时间变化的一个函数关系。为了便于直观的看出速度和航向角随时间变化的关系,要作出了这些航行要素随时间变化的图像:
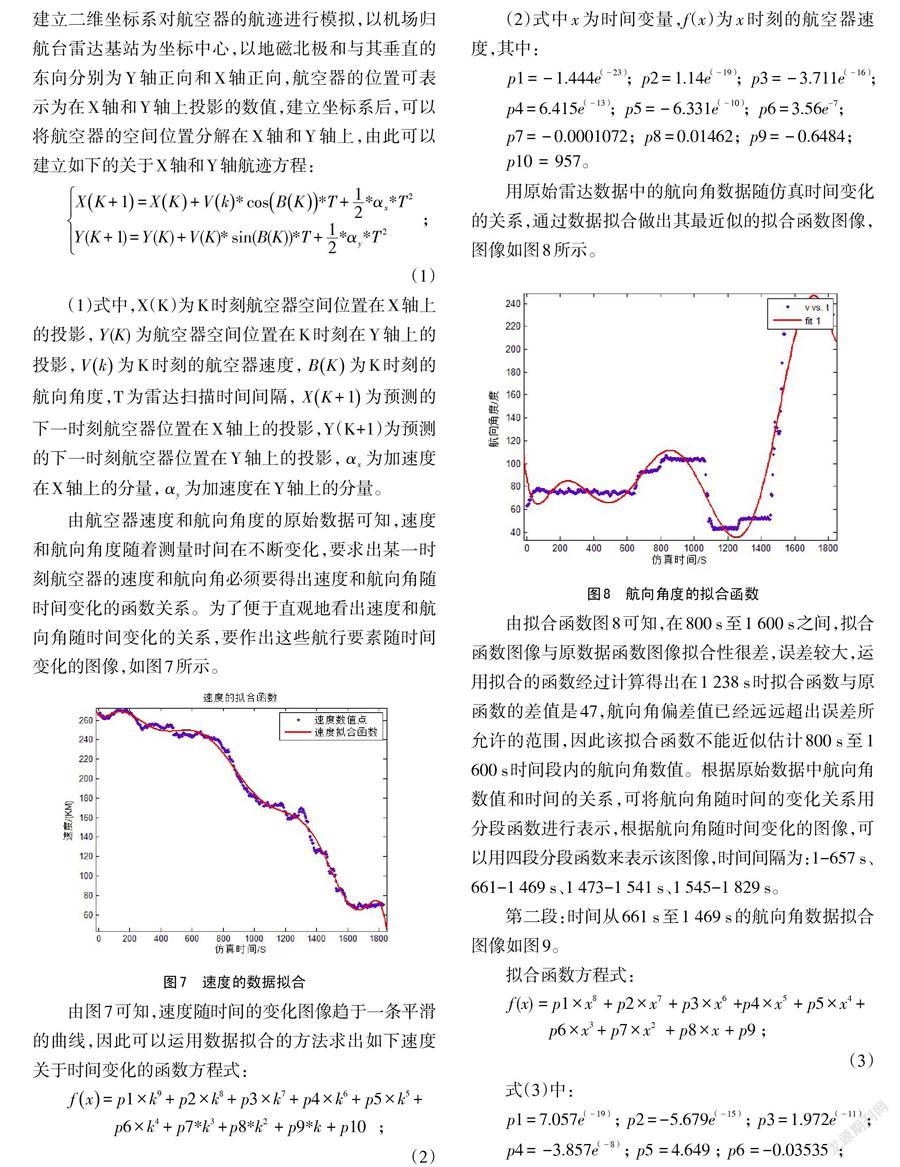
由图4-1可知,速度随时间的变化图像趋于一条平滑的曲线,因此可以运用数据拟合的方法求出如下速度关于时间变化的函数方程式:
用原始雷達数据中的航向角数据随仿真时间变化的关系,通过数据拟合做出其最近似的拟合函数图像,图像如下:
以上拟合函数图4-2可知,在800秒至1600秒之间,拟合函数图像与原数据函数图像拟合性很差,误差较大,运用拟合的函数经过计算得出在1238秒时拟合函数与原函数的差值是47,航向角偏差值已经远远超出误差所允许的范围,因此该拟合函数不能近似估计800秒至1600秒时间段内的航向角数值。根据原始数据中航向角数值和时间的关系,可将航向角随时间的变化关系用分段函数进行表示,根据航向角随时间变化的图像,可以用四段分段函数来表示该图像,时间间隔为:1~657秒、661~1469秒、1473~1541秒、1545~1829秒。
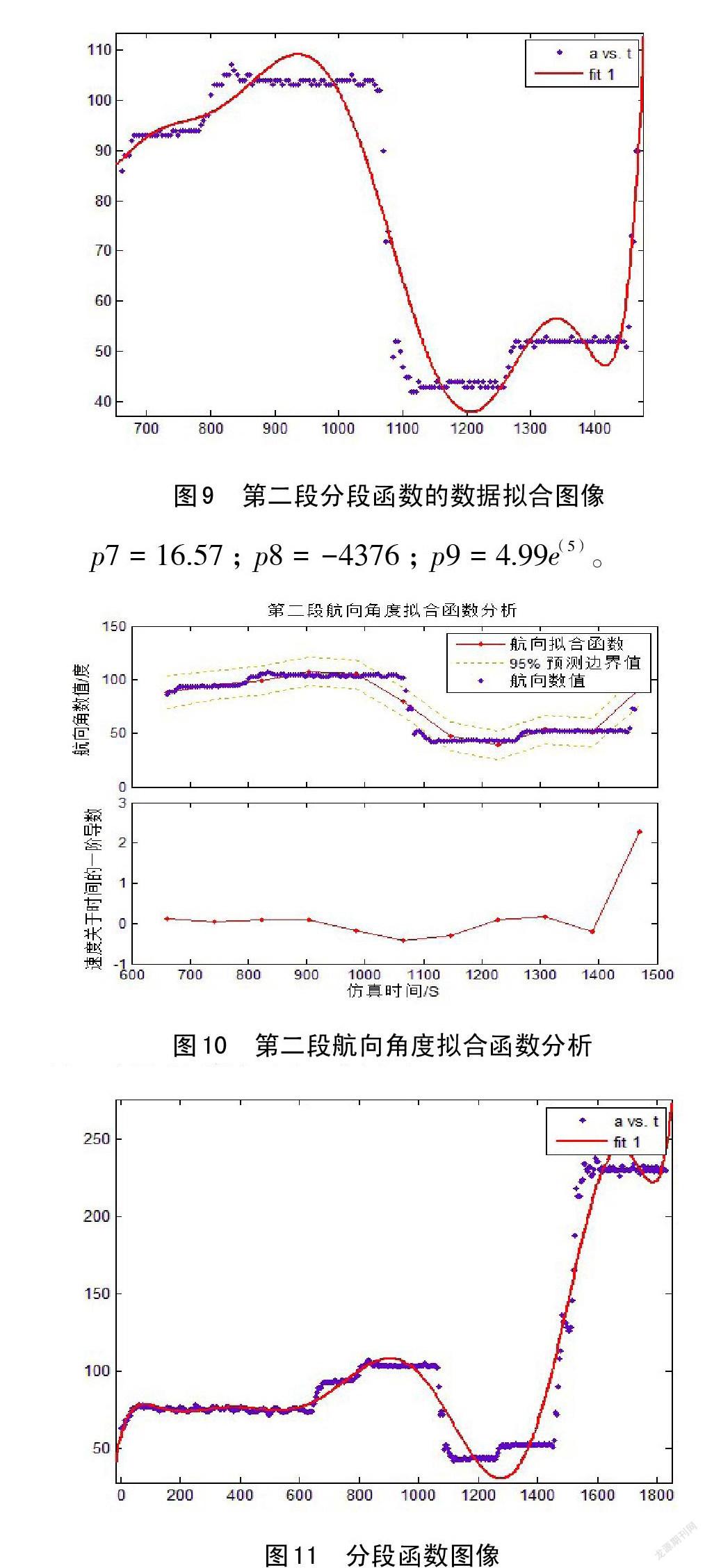
第二段:时间从661秒至1469秒的航向角数据拟合图像如图4-3:
用于第二段拟合函数进行计算,在661秒至1469秒之间最大的航向角度偏差为4度,在允许的偏差范围之内,因此该段拟合函数可以作为航向角度随时间变化的函数。图4-4是第二段拟合函数的数据偏差分析:
按照如上方法可以做出第一段、第三段、第四段航向角度的拟合函数。将四段航向角度的分段函数图像画在一起的图像如图4-5:
4.2 航迹预测仿真
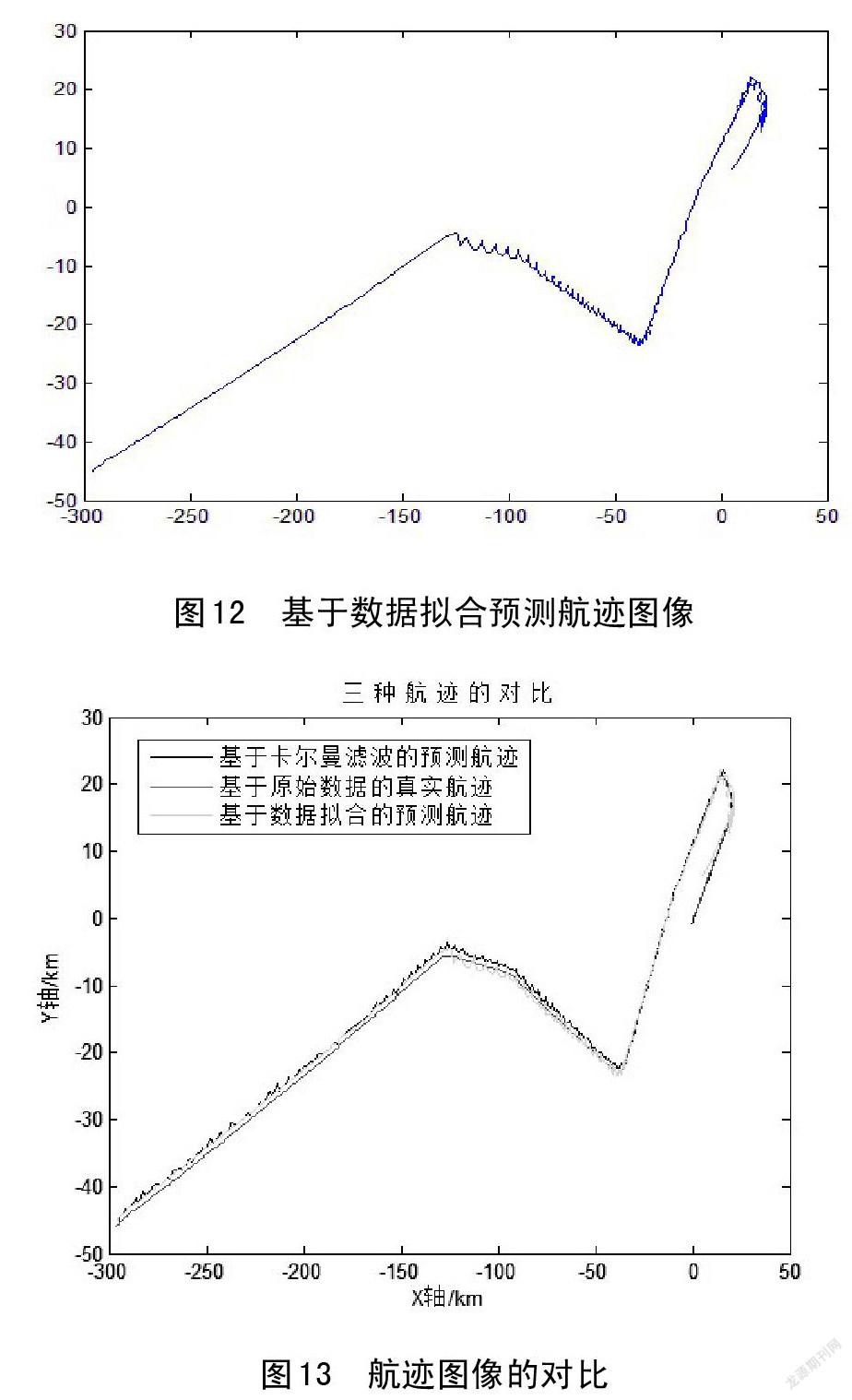
航空器速度和航向角关于时间变化的函数方程式已知,因此在任意时刻K可以根据所得出的方程式求出航空器速度和航向角度的近似值V(K)和B(K);任意时刻K时航空器空间位置X(k)和Y(K)是已知的;T是雷达的扫描时间间隔,一般为4秒。根据这些已知数据,就可以做出基于数据拟合的预测航迹,预测航迹如图4-6:
4.3 数据拟合航迹与原始航迹的对比
数据拟合的航空器飞行航迹与航空器实际飞行航迹进行对比,可以得出预测航迹是否达到了航迹预测精度的要求。对比图像如图4-7所示:
5.结论
通过数据偏差分析,用数据拟合方法做出航空器的航迹时需要提前知道航空器的速度、航向角度的数据值,再利用这些原始数据拟合出速度和航向角度的拟合函数,再用拟合函数进行航迹预测。但是航空器的速度和航向角度在航迹预测前是未知的,且每天的速度和航向角度都是变化的,这个方法并不能进行实际运用,只可以作为航迹数据的分析。数据拟合出的航迹在航空器保持航向不变飞行时,其航迹与原始数据的航迹拟合度较高,当航空器航向发生改变时,基于数据拟合的航迹与原始数据的航迹偏差较大,预测出的航迹会出现较大的波动和跳跃。
参考文献
[1] Paielli R A. Trajectory specification for high capacity air traffic control: U.S. Patent 7,650,232[P]. 2010-1-19.
[2] Prevost C G, Desbiens A, Gagnon E. Extended Kalman filter for state estimation and trajectory prediction of a moving object detected by an unmanned aerial vehicle[C]//American Control Conference, 2007. ACC'07. IEEE, 2007: 1805-1810.
[3] 谢丽,张军峰,隋东等.基于交互式多模型滤波算法的航迹预测[J].航空计算技术,2012,42(5):68-70.
[4] Lee H P, Leffler M F. Development of the L-1011 four-dimensional flight management system[M]. National Aeronautics and Space Administration, Scientific and Technical Information Office, 1984
[5] 王超, 郭九霞, 沈志鹏. 基于基本飞行模型的 4D 航迹预测方法[J]. 西南交通大学学报, 2009, 44(2): 295-300.
余娇(1989——),女,漢族,陕西紫阳人,大学本科,助理工程师,主要从事民航空中交通管制工作。
