互层倾倒边坡岩层折断深度对挠度的影响分析

程传阁　陈梁　吕敬清　余成　韦志远

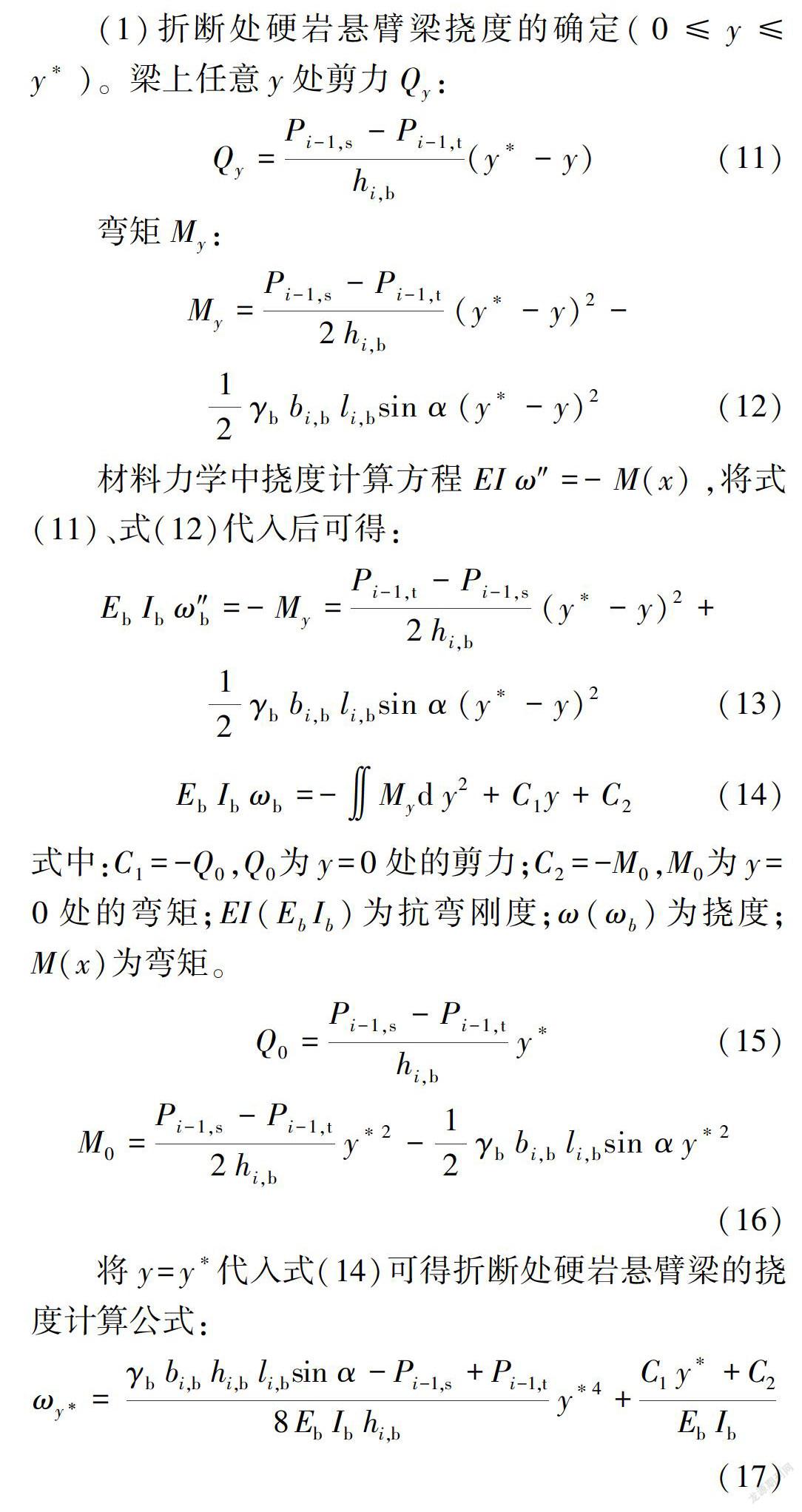
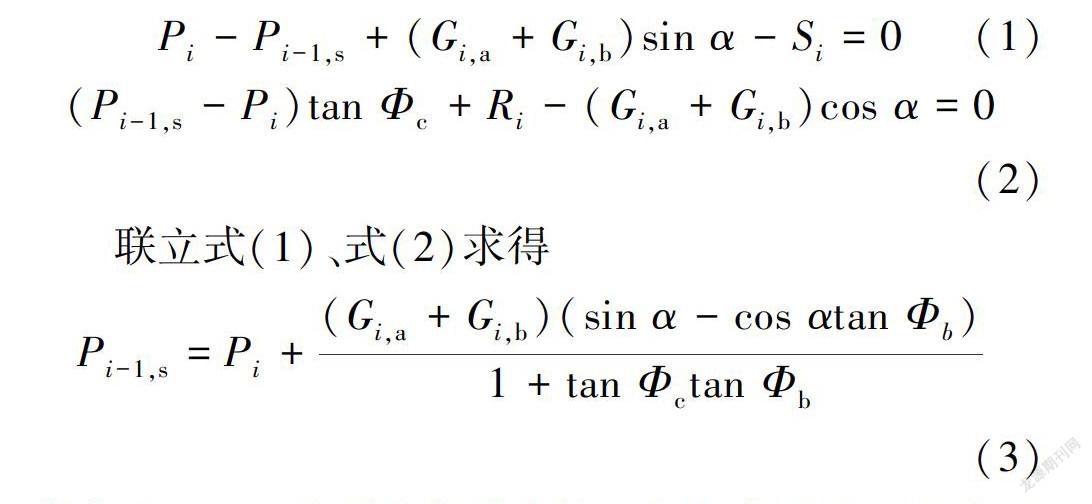
摘要：针对互层反倾岩质边坡倾倒破坏问题，在综合考虑软岩和硬岩力学性质差异的基础上提出了“组合悬臂梁”模型，并对各悬臂梁进行了力学分析。依据最大拉应力破坏准则建立平衡方程，计算出硬岩岩层的折断深度，并利用“分段叠加法”给出了组合岩层坡表处挠度计算公式。根据澜沧江苗尾水电站库区左岸一典型反倾软硬互层岩质边坡岩体参数，研究折断深度对组合岩层挠度的影响，结果表明：硬岩岩层折断深度越大组合岩层坡表处挠度越大;折断深度一定时，随着软岩与硬岩厚度比的增大、弹性模量比减小，组合岩层挠度增大：组合岩层挠度较大区域集中在岩层倾角60。附近，推测组合岩体岩层倾角接近60。时容易发生倾倒变形。

关键词：组合悬臂梁模型;折断深度;挠度;倾倒岩体

中图分类号：P642.4

文献标志码：A

doi：10.3969/j.issn. 1000- 1379.2019. 04.028

边坡倾倒破坏是反倾岩质边坡的主要破坏模式之一，广泛存在于水利水电、铁路、矿山等工程边坡中，是边坡治理的重点之一。对于反倾岩质边坡倾倒问题国内外学者进行了大量研究，Goodman等[1]最早将极限平衡分析法引入倾倒边坡岩体理论分析中，该方法将倾倒体看作由若干等宽矩形条块组成的离散集合体，通过对单个条块的力学分析将倾倒边坡从坡顶到坡脚依次划分为稳定区、倾倒区、滑动区;Aydan等[2]提出了反倾岩质边坡基于极限平衡理论的悬臂梁弯曲倾倒模型，通过对模型的力学简化分析和迭代方法研究，建立了利用坡脚剩余下滑力评价边坡稳定性的理論：Adhikary等[3]通过一系列试验和力学分析对Aydan等提出的悬臂梁弯曲极限平衡理论进行了验证和推广：卢海峰等[4]在Aydan等提出的理论基础上对岩体参数、层间作用力和折断面形态等进行了修正，提出了利用层间剩余不平衡力评价边坡稳定性的理论，同时对影响边坡稳定的因素进行了理论分析：陈红旗等[5]将单个岩层简化为悬臂梁模型，考虑悬臂梁在临空条件下受重力和侧向压力作用，推导出岩层的最小折断深度和折断处的挠度，通过对比计算出的挠度值和实测挠度值，判断岩层是否发生了折断破坏;郑允等[6]通过对荷载作用下反倾边坡岩层3种倾倒力学模型的对比分析，提出了荷载作用下反倾边坡的倾倒一滑移破坏模式。目前国内外学者对反倾岩质边坡的倾倒力学机制研究取得了一定成果，但在进行研究时往往将研究对象简化为一种岩性岩体，实际上边坡岩体常呈互层状，且各层岩性差异较大，变形破坏模式不一，已有的力学模型难以揭示反倾互层倾倒岩体的变形规律，需建立新的模型和理论。

本文根据Aydan等提出的基于极限平衡理论的悬臂梁弯曲倾倒模型，综合考虑软岩和硬岩的力学性质，将硬岩和软岩分别简化为以脆性折断和塑性弯曲破坏为主的“组合悬臂梁”模型，抽取倾倒体内具有代表性的组合岩层进行力学分析，根据最大拉应力破坏准则计算出硬岩的折断深度，利用“分段叠加法”推导出组合岩层坡表处挠度的计算公式，并就硬岩折断深度对组合岩层挠度的影响进行了分析。

1 简化计算模型建立及岩层力学分析

1.1 简化计算模型建立

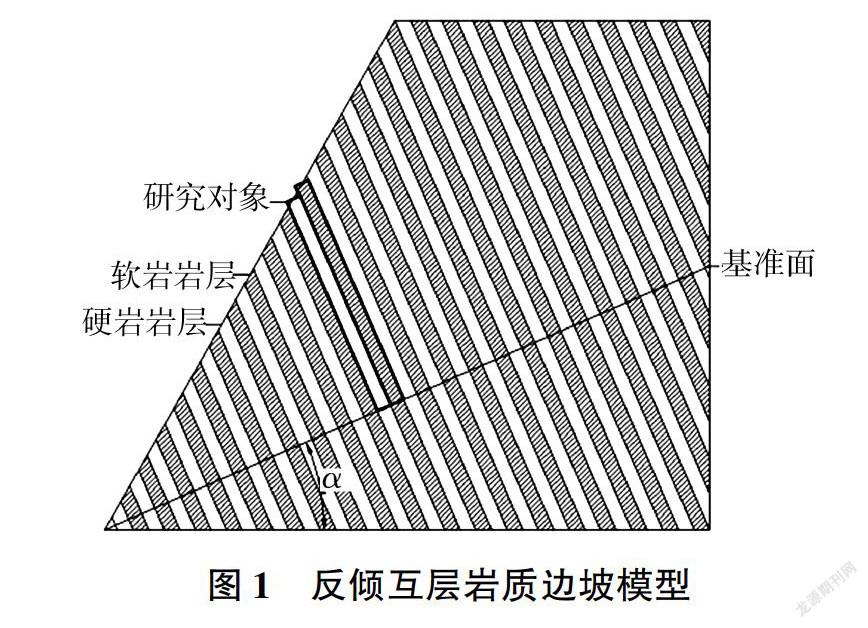
在卸荷、风化、荷载等作用下，倾倒边坡岩体结构复杂，难以进行力学推导分析，因此建立简化反倾互层边坡模型（见图1，α为基准面与水平面夹角），并从边坡模型中抽取具有代表性的组合岩层进行力学分析。

由于研究的重点是互层边坡折断深度与岩层挠度的关系，而岩体力学参数的各向异性影响力学公式的求解，但对研究问题影响不大，因此在进行力学分析时对边坡进行了适当简化：

（1）假设一坡脚走向与岩层走向一致的基准面，基准面与岩层层面垂直，倾倒岩层的根部位于基准面上[2]。

（2）假设岩层为均质材料，相同岩性岩层物理力学参数相同，考虑岩层中节理裂隙对岩体质量的劣化作用对岩层物理力学参数进行适当折减，将折减后的参数作为同一岩性岩层的参数。岩性相同且相邻的岩层按一层考虑，厚度为各岩层厚度之和。

（3）为了便于模型受力分析，在进行力学推导计算时，不同岩性岩层间法向应力简化为集中力，其大小为均布力总和，作用点在各接触面中点处[7-10]，岩层间内摩擦角为定值。

1.2 组合悬臂梁力学分析思路

组合悬臂梁的力学平衡分析按先整体后局部的思路进行。为了便于未知量的求解，根据组合悬臂梁的受力情况将组合悬臂梁先看作一个整体进行受力分析，建立平衡方程，求得组合梁间力的作用关系，为最小折断深度及组合岩层坡表处挠度的求解提供依据。由于组合梁间力的求解需建立弯矩方程，因此要考虑软岩悬臂梁和硬岩悬臂梁的变形顺序。根据岩体力学知识，软岩的抗弯刚度比硬岩的抗弯刚度小，可认为组合悬臂梁中软岩悬臂梁最先有弯曲变形趋势，因此可以利用软岩悬臂梁的弯曲力矩等于抗弯力矩的临界状态建立弯矩方程。

1.2.1 组合悬臂梁整体受力分析

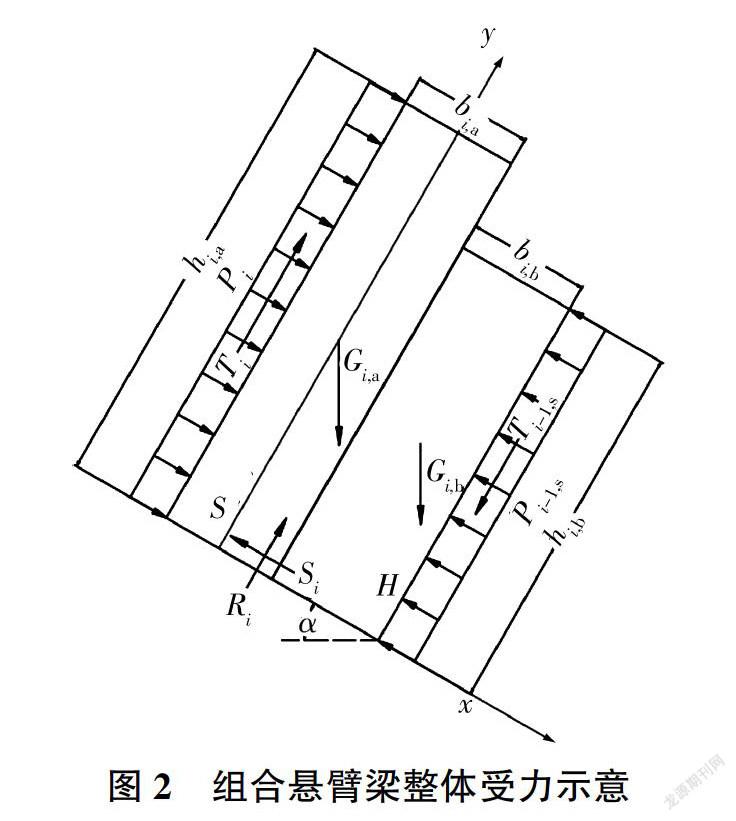
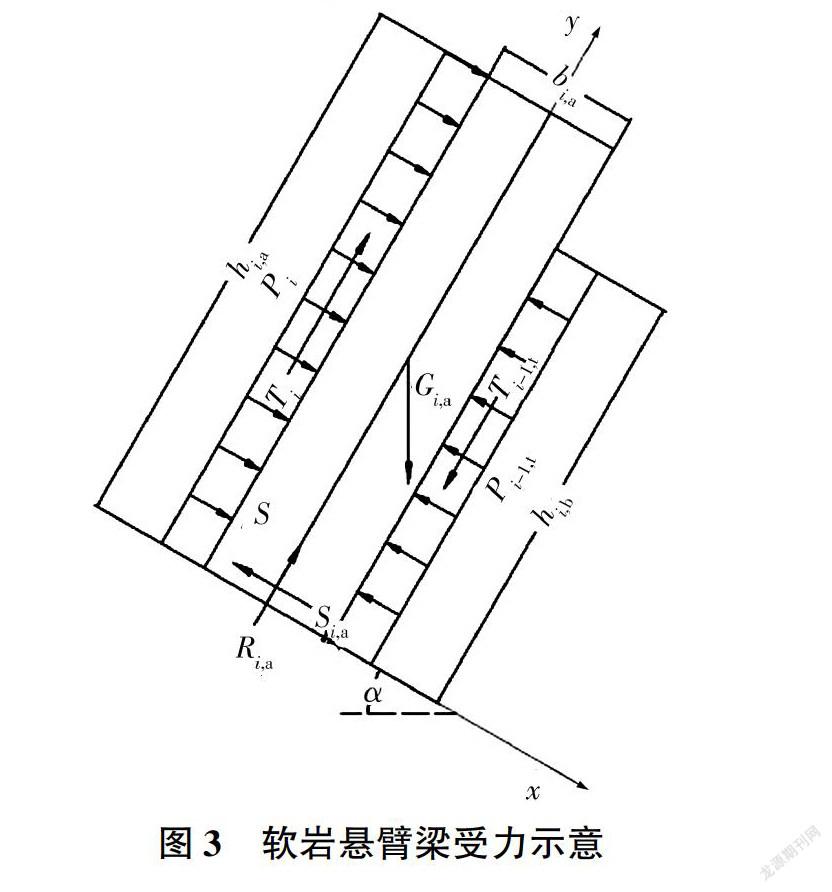
在反倾互层边坡成坡过程中附加应力几乎已释放完毕[11].因此组合梁在空间上主要受上覆岩层的推力、自身重力、与基准面间摩阻力和下覆岩层的支撑力作用。为便于建立力学平衡方程，建立如图2所示的坐标系，其中坐标原点位于基准面上软岩岩层中轴线处，S为软岩岩层，H为硬岩岩层。初始状态，组合悬臂梁x方向和y方向所受合力为0，可建立如下方程组：

2.2 组合悬臂梁挠度

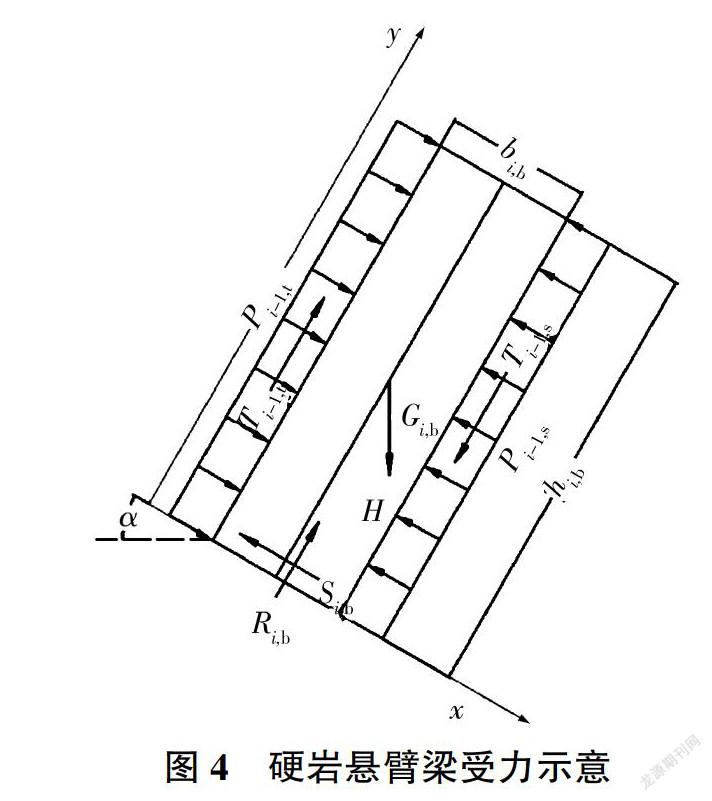
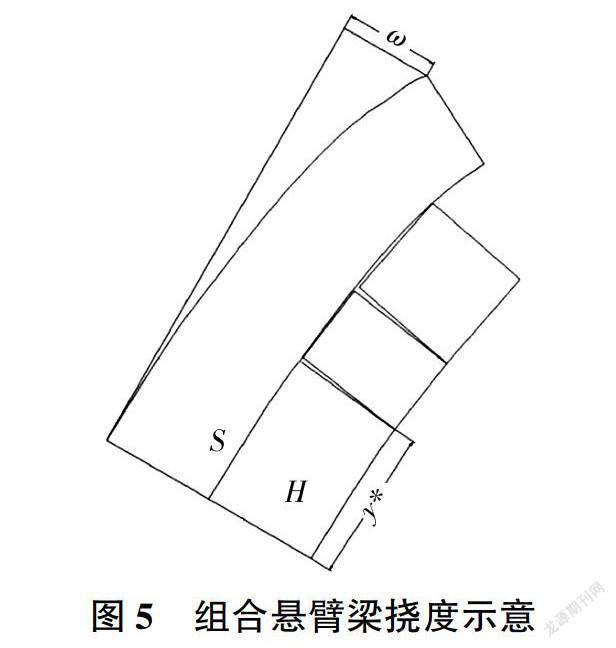
悬臂梁挠度的求解方法目前有变形能量法和直接由弯矩求得的方法，本文对岩层挠度的计算采用直接由弯矩求得的方法[5]。在硬岩悬臂梁发生折断破坏之前，组合梁以硬岩悬臂梁发生相对较小的变形为主，未折断的硬岩悬臂梁在整个组合悬臂梁中为“关键层”，起到“托板”的作用，即抵抗上覆软岩发生塑性变形，此段硬岩岩层力臂较大，承受上覆岩层作用力大，产生的弯曲变形不可忽略，因此此段将硬岩悬臂梁挠度作为组合岩层挠度判别标准。折断后的硬岩岩层在层间剪切挤压作用下断裂成硬岩岩块，绕一点发生转动，基本不发生弯曲变形，此时组合梁变形以软岩变形为主，将软岩坡表处挠度作为组合岩层挠度判别标准，对组合悬臂梁挠度进行分段叠加计算。组合悬臂梁挠度示意见图5（ω为挠度）。

3 组合岩层挠度影响因素分析

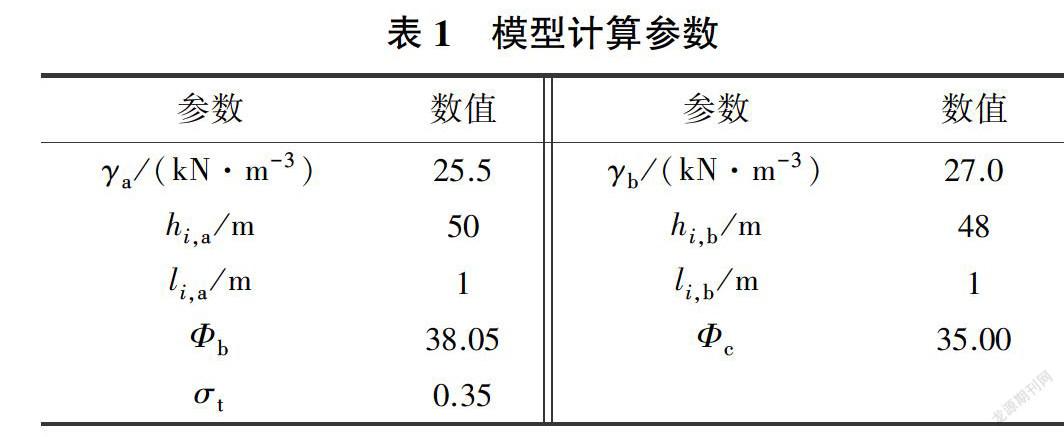
通过以上分析可以看出，硬岩岩层折断深度与组合岩层挠度的计算有相关性，此外，岩层厚度、岩层倾角、岩层力学性质的差异也影响挠度的计算，因此选取澜沧江苗尾水电站库区某典型互层倾倒边坡岩体参数（见表1）建立概化模型，分析折断深度分别为10、20、30、40、50 m等5种情况下组合岩层中软岩与硬岩厚度之比、弹性模量比及岩层倾角对组合岩层挠度的影响。计算时将各物理量依次代人式（3）、式（5）、式（10），联立求得层间力，代入式（24）求得组合巖层坡表处挠度。在分析时采用MATLAB软件对复杂公式进行求解和计算。

3.1 岩层厚度比对组合岩层挠度的影响

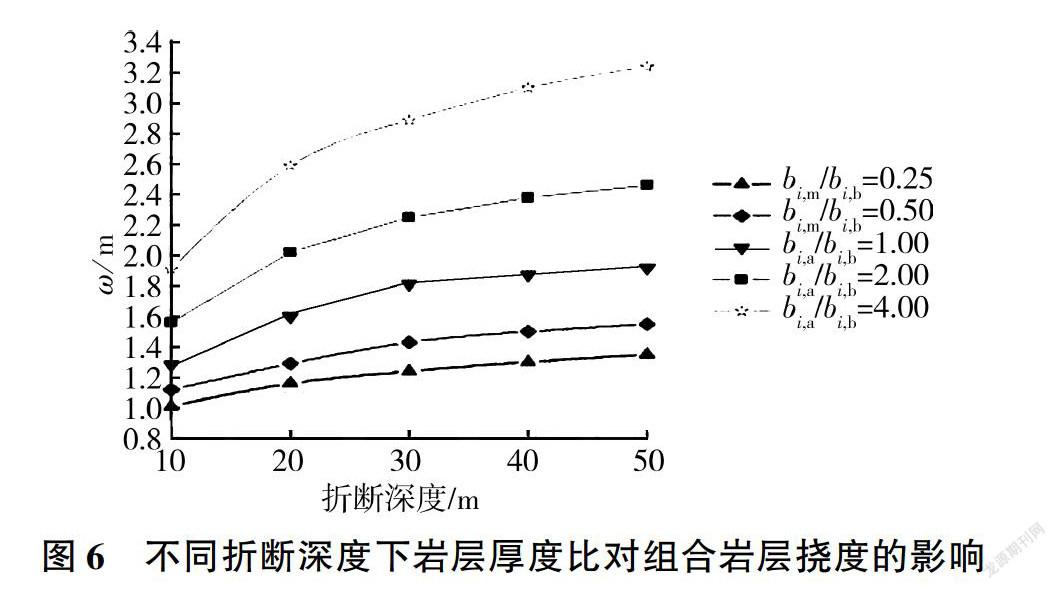
考虑到计算分析的复杂性，选取硬岩岩层厚度b =0.5 m，分析b/b分别为0.25、0.50、1.00、2.00、4.00时，硬岩折断深度对组合岩层挠度的影响，计算结果见图6。

由图6可以看出，硬岩岩层折断深度对组合岩层挠度的影响受岩层厚度比控制，随着软岩岩层厚度所占比重的增大，组合岩层挠度增大，其原因是，组合岩层的倾倒破坏与硬岩岩层的抵抗弯曲折断作用有很大关系，硬岩岩层厚度的减小极大削弱了组合岩层承受弯矩能力，这与陈从新等[15]提出的随着岩层厚度的减小，岩层抗倾倒折断能力急剧降低的结论一致。从组合岩层挠度变化趋势看，岩层厚度比较小时，组合岩层挠度随硬岩岩层折断深度的增加近似呈线性缓慢增大，说明此时组合岩层抗弯折能力较强，组合岩层破坏以硬岩岩层变形为主。随着硬岩岩层厚度所占比重的减小，组合岩层失去抗弯折优势，变形加剧。折断深度对组合岩层挠度的影响，岩层厚度比是一个重要因素，软岩厚度占的比重越大，组合岩层挠度越大。

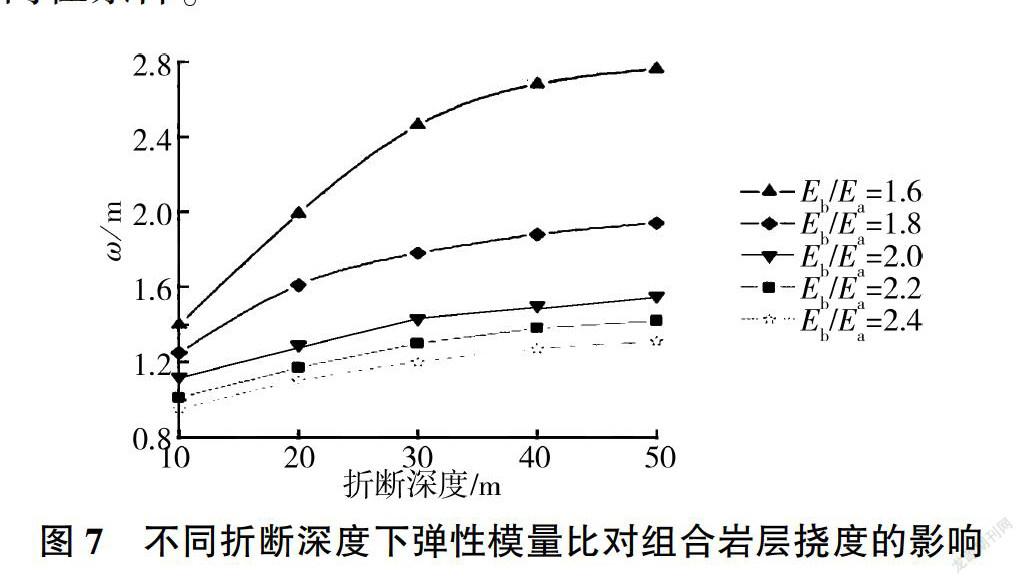
3.2 岩层弹性模量比对组合岩层挠度的影响

选取硬岩岩层弹性模量Eb =0.85 GPa，研究E/E分别为1.6、1.8、2.0、2.2、2.4等5种情况下硬岩折断深度对组合岩层挠度的影响，计算结果见图7。岩层弹性模量是衡量材料发生弹性变形情况的一个重要指标，由图7可以看出，组合岩层挠度与弹性模量比有关，硬岩岩层与软岩岩层弹性模量比小于2.0时，随着硬岩折断深度的增加组合岩层的整体挠度快速增大：弹性模量比大于2.0时，随着硬岩折断深度的增加组合岩层的整体挠度增大的幅度较小。说明硬岩岩层刚度越大（即弹性模量越大）组合岩层抵抗折断能力越强，当组合岩层发生一级折断后，其中的硬岩岩层刚度越大，发生次一级折断的可能性越小，组合岩层挠度也越小，即岩层岩性特点是岩层发生倾倒破坏的基础及内在条件。

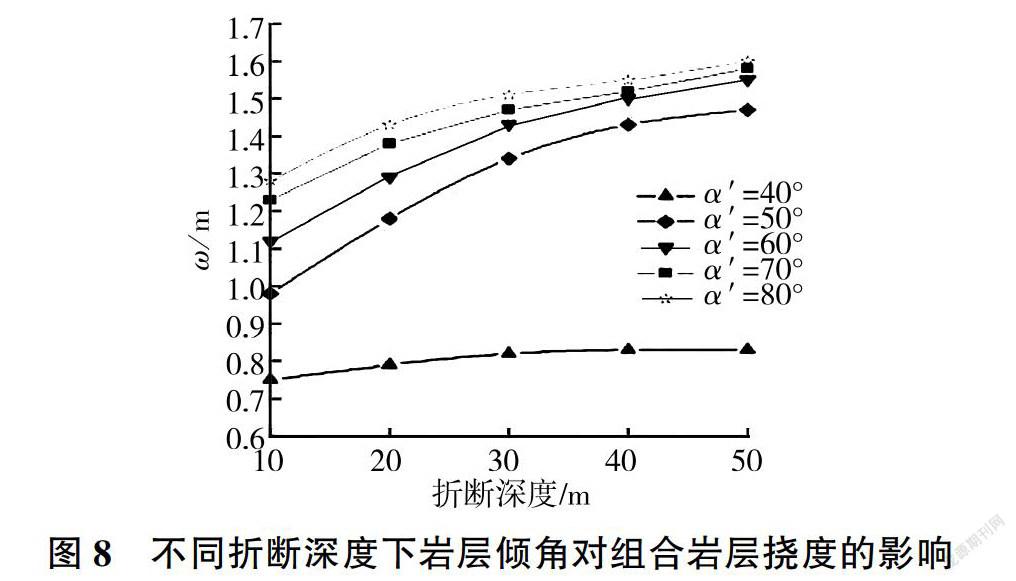
3.3 岩层倾角对组合岩层挠度的影响

根据图2中几何关系可知，岩层倾角α’= 90° -α。岩层发生倾倒破坏与岩层倾角有密切联系，因此选取岩层倾角分别为40°、50°、60°、70°、80°研究硬岩折断深度对组合岩层挠度的影响，计算结果见图8。由图8可以看出，随着硬岩折断深度的增加组合岩层的整体挠度呈增大趋势，且陡倾角岩层更容易发生倾倒破坏。岩层倾角为40° - 60°时，组合岩层的挠度变化较大，推测在40° - 60°存在一临界角度控制着挠度增长速率的突变：岩层倾角大于60°时，组合岩层挠度虽有所增大，但增量相对较小，说明倾倒岩层在60°左右易发生倾倒破坏。该结论与左保成等[16-18]研究反倾岩质边坡发生倾倒时岩层倾角临界值及危险值范围有很好的一致性。此外，对比岩层厚度比与岩层倾角对组合岩层挠度的影响发现，岩层厚度比对组合岩层挠度的影响更为显著，曲线更为分散，与陈从新等[15]利用数值模拟研究岩层倾倒影响因素时提出的边坡变形对岩层厚度更为敏感的结论一致。

4 结语

反倾互层岩质边坡岩层倾倒破坏程度与岩层岩性差异有很大关系，岩层抗弯刚度、不同岩性岩层厚度分配等都影响组合岩层的倾倒破坏。组合岩层坡表处挠度与硬岩岩层折断深度有直接关系，折断深度越大组合岩层坡表处挠度越大。

本文从建立简化模型和理论推导的角度研究了硬岩岩层折断深度对组合岩层挠度的影响，但未考虑卸荷、地震、蓄水等外力作用，因此计算出的挠度较实际挠度小。

参考文献：

[1]COODMAN R E，BRAY J W.Toppling of Rock Slope[ C]//Proceeding of the Speciality Conference on Rock Engineeringfor Foundations and Slopes. Bouider：ASCE，1976： 202-234.

[2]AYDAN 0，KAWAMOTO T.The Stability of Slopes and Un-derground Openings Against Flexural Toppling and Their Sta-bilization[ J]. Rock Mechanics and Rock Engineenng，1992，25（3）：143-165.

[3]ADHIKARY D P，DYSKIN A V.A Study of the Mechanismof Flexural Toppling Failure of Rock Slopes[ J]. Rock Me-chanics and Rock Engineering， 1997， 30（2）：145-165.

[4] 卢海峰，刘泉声，陈从新，反倾岩质边坡悬臂梁极限平衡模型的改进[J].岩土力学，2012，33（2）：577-584.

[5] 陈红旗，黄润秋，反倾层状边坡弯曲折断的应力及挠度判据[J].工程地质学报，2004，12（2）：243-246.

[6]郑允，陈从新，刘婷婷，等，坡顶荷载作用下岩质边坡倾倒 破坏分析[J].岩土力学，2015，36（9）：2640-2647.

[7] 张以晨，佴磊，沈世伟，等，反倾层状岩质邊坡倾倒破坏力学模型[J].吉林大学学报（地球科学版），2011，41（增刊1）：207-213.

[8] 刘顺昌，如美水电站岩质边坡倾倒破坏机理研究[D].武汉：中国地质大学，2013：18-26.

[9]位伟，段邵辉，姜清辉，等，反倾边坡影响倾倒稳定的几种因素探讨[J].岩土力学，2008，29（增刊）：432-434.

[10] 刘海军，赵建军，巨能攀，岩质边坡倾倒破坏的力学分析[J].岩土力学，2016，37（增刊1）：289-294.

[11]COODMAN R E，BRAY J W.‘roppling of Rock Slopes [J].American Society of Civil Engineers， 1976（2）： 201-234.

[12] 蔡静森，均质等厚反倾层状岩质边坡倾倒变形机理研究[D].武汉：中国地质大学，2013：16-25.

[13] 赵建军，马运韬，蔺冰，等，平缓反倾采动滑坡形成的地质力学模式研究：以贵州省马达岭滑坡为例[J].岩石力学与工程学报，2016，35（ 11）：2218-2224.

[14] 陈维，徐则民，刘文连，差异风化型危岩力学模型及破坏机制研究[J].岩土力学，2015，36（1）：196-204.

[15] 陈从新，郑允，孙朝燚，等，岩质反倾边坡弯曲倾倒破坏分析方法研究[J].岩石力学与工程学报，2016，35（ 11）：2174-2187.

[16]左保成，陈从新，刘小巍，等，反倾岩质边坡破坏机理模型试验研究[J].岩石力学与工程学报，2005，24（19）：3505-3510.

[17] 程东幸，刘大安，丁恩保，等，层状反倾岩质边坡影响因素及反倾条件分析[J].岩土工程学报，2005，27（ 11）： 127-131.

[18] 李明霞，董联杰，层状反倾边坡变形特征及影响因素分析[J].计算力学学报，2015，32（6）：831-837.

【责任编辑吕艳梅】