组合梁考虑滑移效应的理论分析

肖岩+彭罗文

摘 要：钢混凝土组合梁的刚度和挠度分析因可能受到两者界面的相对滑移影响而十分复杂.针对组合梁受界面滑移效应的影响，进行了静力线弹性分析，提出了组合梁挠度计算的二阶算法，分别建立了关于组合梁考虑滑移效应的挠度和层间相对滑移的二阶常微分方程，给出了相应的边界条件，求得了简支梁、悬臂梁、两端固定梁和一端简支一端固定梁4种不同边界条件组合梁在不同荷载作用下的层间相对滑移和挠度的理论精确解，并给出了组合梁受层间滑移效应影响的内力计算.通过与组合梁挠度计算高阶算法的对比，二阶算法简化了组合梁考虑滑移效应的挠度计算，给出了相对全面的计算结果.

关键词：组合梁；滑移效应；挠度

中图分类号：TU398.9 文献标志码：A

组合梁具有刚度大、承载能力高等优点，在建筑结构、桥梁结构等领域得到了广泛应用[1].然而，广泛应用于实际工程的栓钉等柔性抗剪连接件由于受到钢梁与混凝土翼缘板之间水平剪力的作用而产生变形，引起交界面产生滑移，从而使组合梁刚度降低，挠度也相应增大.因此，相对精确的计算正常使用极限状态下组合梁考虑滑移效应的挠度十分重要.

国内外众多专家学者对组合梁的滑移效应和挠度计算等进行了深入研究[2]，在大量实验研究和理论分析的基础上提出了各种不同的滑移、内力和挠度等计算方法.Newmark等[3]进行了组合梁考虑滑移效应线弹性分析的早期研究.Girhammar 和Gopu[4]对组合梁进行了内力分析，建立了关于组合梁考虑滑移效应挠度的六阶常微分方程.聂建国等[5]在理论分析的基础上建立了简支梁界面滑移微分方程，给出了简支梁变形计算的一般公式，并提出了组合梁变形计算的折减刚度法[6].尽管在其推导过程中附加曲率取层间相对滑移应变与组合梁高度之比Δφ=εs/h值得商榷，另外取e-αL≈0也会造成一定程度的誤差，但是，折减刚度法使得组合梁的设计变得简洁，从而促进了其推广应用.朱聘儒[7]对简支梁在均布荷载作用下的挠度计算进行了分析计算.童根树等[8]建立了简支梁均布荷载作用下的高阶微分方程，得到了简支梁的挠度计算公式.Girhammar 和Pan[9]通过虚功原理建立了组合梁挠度计算的微分方程，得到了组合梁挠度计算的一般表达式.在此基础上，Girhammar[10]提出了组合梁考虑滑移效应静力计算的简化方法.蒋丽忠等[11]在Goodman弹性夹层假设和弹性体变形理论的基础上，对简支组合梁在均布荷载作用下的界面滑移和挠度计算进行了分析研究， 推导出了简支组合梁的界面滑移和挠度的计算公式.余志武等[12]给出了简支组合梁在集中荷载作用下的界面滑移和挠度的理论计算公式.苗林和陈德伟[13]利用Goodman 弹性夹层法分析了双层组合梁在弹性工作阶段的滑移、内力及挠度与荷载之间的关系.胡夏闽等[14]采用曲率等效原则提出了组合梁挠度计算的附加曲率法.

组合梁考虑滑移效应的各个计算方法都有各自的特点和适用范围，其中部分计算方法只对简支梁进行了分析计算，并未考虑其他边界条件的组合梁，尤其是对超静定梁精确解的计算.同时我国《钢结构设计规范》（GB50017—2003）[15]中，会出现随剪力连接程度的增大组合梁考虑滑移效应的折减刚度B反而减小，挠度反而增大的反常情况，这些问题都值得进一步的分析研究与对比.本文选取组合梁中任一微元体为研究对象进行详细的静力线弹性分析，建立组合梁考虑滑移效应的二阶算法来简化组合梁的挠度计算，分别建立挠度和层间相对滑移的二阶常微分方程，并与组合梁考虑滑移效应挠度计算的高阶算法进行对比.利用二阶算法通过相应的边界条件，求得4种不同边界条件组合梁的挠度，同时给出组合梁受到层间滑移影响的内力计算.

1 组合梁微分方程的建立

组合梁考虑滑移效应理论分析的基本假设：

1） 组合梁各个子构件材料均为线弹性，挠度均为小变形；

2） 组合梁剪力连接件均匀布置，交界面上的层间滑移力与层间相对滑移成正比；

3） 组合梁各个子构件之间不会发生竖向剥离，各个子构件的曲率和挠度均相等；

4） 组合梁各个子构件均不考虑剪切变形，并分别符合平截面假定.

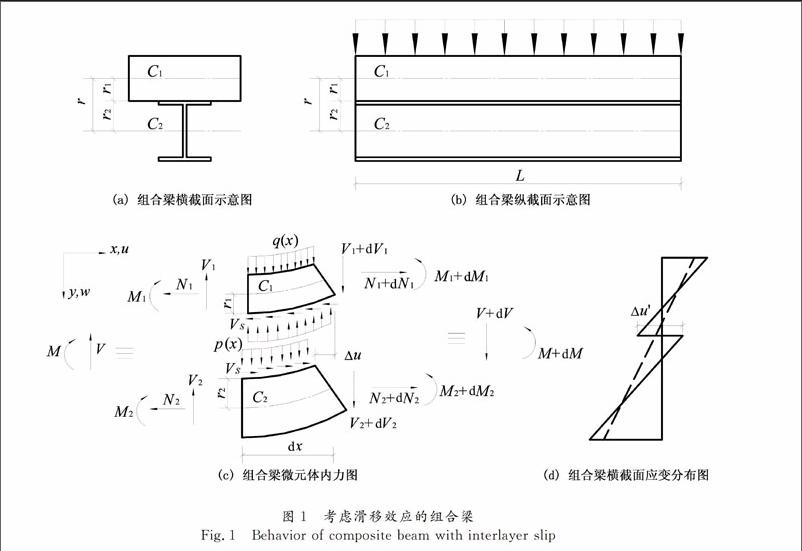
组合梁由子构件1和子构件2通过剪力连接件连接而成，取组合梁一微元体进行受力分析，如图1所示.在任意荷载q（x）作用下，组合梁横截面如图1（a）所示，组合梁纵截面如图1（b）所示，组合梁微元体内力如图1（c）所示，组合梁横截面应变分布如图1（d）所示，其中不考虑滑移效应的应变分布用虚线表示，考虑滑移效应的应变分布用实线表示.组合梁及其子构件1和2所受轴力、剪力、弯矩、层间滑移力以及层间掀起力分别表示为N，V，M，VS和p（x），其中下标1和2分别表示子构件1和2.组合梁沿坐标轴x和y方向的位移分别表示为u和w.子构件1和2的中性轴位置分别表示为C1和C2.子构件1和2中性轴到其交界面的距离分别表示为r1和r2，子构件1和2中性轴之间的距离表示为r，其中r= r1+ r2.子构件1和2之间的层间相对滑移表示为Δu.各个物理量的正方向均如图1所示.

式中：Acf为混凝土翼缘板的横截面面积；Icf为混凝土翼缘板的横截面惯性矩；A为钢梁的横截面面积；I为钢梁的横截面惯性矩；dc为钢梁横截面与混凝土翼缘板横截面的形心距；h为组合梁高度；l为组合梁跨度；p为抗剪连接件平均纵向间距；k为连接件的刚度系数；ns为连接件的列数；αE为钢材相对于混凝土材料的弹性模量之比.

由公式（66）～（73），折减刚度B采用本文统一符号可表示为：

B=EI

SymboleB@ 1+18αL2·EI0EI

SymboleB@ 0.4-30.81αL2（74）

规范的挠度放大系数Φ采用本文统一符号可表示为：

Φ=1+18αL2·EI0EI

SymboleB@ 0.4-30.81αL2（75）

由公式（74）可知，折减刚度B随着组合效应系数αL变化呈现抛物线变化.当αL≤3.38时，折减刚度B为负值，显然错误，虽然规范中规定当ζ≤0时，取ζ=0，但缺乏相关理论依据；当3.38≤αL≤4.78时，折减刚度B随剪力连接程度（即组合效应系数αL）的增大反而减小，可见规范存在不合理之处.

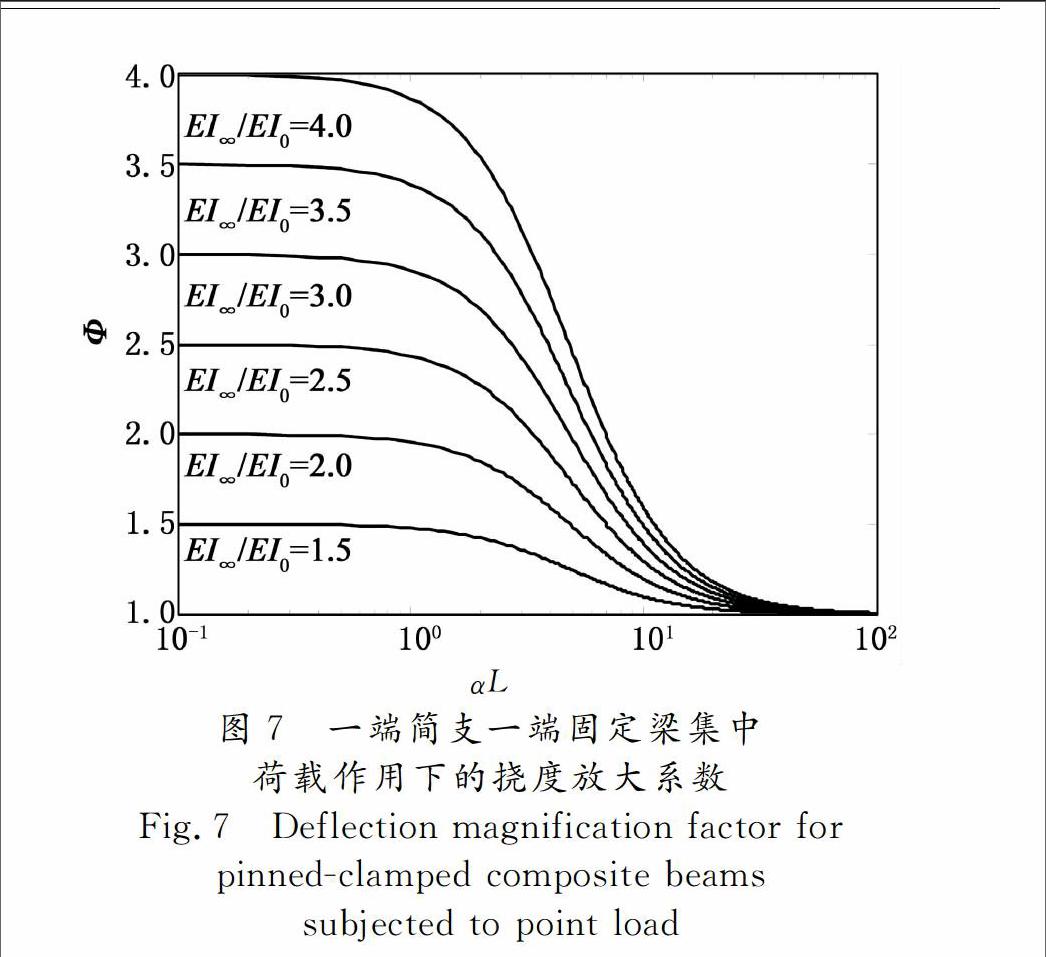
由公式（66）和表1可得，集中荷载作用下，4种不同边界条件组合梁的挠度放大系数Φ如图4～图7所示，组合梁完全剪力连接与完全无剪力连接的刚度比EI

SymboleB@ /EI0如图4～图7所示.

由图4～图7可知，对于4种不同边界条件的组合梁，当组合效应系数αL趋于0时，挠度放大系数Φ趋于刚度比EI

SymboleB@ /EI0，组合梁趋于完全无剪力连接；当组合效应系数αL不断增大，即剪力连接程度不断增大时，挠度放大系数Φ趋于1，组合梁趋于完全剪力连接.满足组合梁的两种极限状态现象：完全无剪力连接与完全剪力连接.

规范中折减刚度是在简支梁的求解基础上得到的，并没有针对其他边界条件的组合梁进行相关说明，因此不能应用于其它边界条件的组合梁.图4中，采用规范的挠度放大系数与精确解相差较大，可见我国规范相关内容有待进一步补充与改进.

6 结 论

本文针对组合梁受界面滑移效应的影响，进行了静力线弹性分析，建立了组合梁考虑滑移效应的微分方程，得到了以下结论：

1） 建立了组合梁挠度计算的二阶算法.建立了分别关于组合梁考虑滑移效应挠度w和层间相对滑移Δu的二阶常微分方程，并且给出了相应的边界条件.

2） 组合梁挠度计算的二阶算法可将组合梁考虑滑移效应挠度w中由于滑移效应产生的附加挠度Δw单独分离出来进行计算.同时，在计算过程中计算求得出了组合梁的层间相对滑移Δu，对于研究组合梁的滑移效应提供了一个重要的参数.

3） 本文提出的二阶算法简化了组合梁考虑滑移效应的挠度计算，与以往文献中的高阶算法相比具有更好的优越性，建议采用组合梁挠度计算的二阶算法进行相关分析计算.

4） 建立了组合梁考虑滑移效应的内力计算公式.

5） 给出了相对严密和全面的挠度计算结果，求得了4种不同边界条件组合梁挠度和层间相对滑移的理论精确解.

参考文献

[1] 毛小勇， 肖岩. 标准升温下轻钢-混凝土组合梁的抗火性能研究[J]. 湖南大学学报： 自然科学版， 2005， 32（2）： 64-70.

MAO Xiaoyong， XIAO Yan. Behavior of lightweight steelconcrete composite beams subjected to standard fire [J]. Journal of Hunan University： Natural Sciences， 2005， 32（2）： 64-70. （In Chinese）

[2] 邵旭東， 刘俊珂. 计入加劲肋的圆孔蜂窝组合梁强度简化计算[J]. 湖南大学学报： 自然科学版， 2009， 36（9）： 7-11.

SHAO Xudong， LIU Junke. Reduced computation of the strength of circular hole castellated composite beams with stiffened webs [J]. Journal of Hunan University： Natural Sciences， 2009， 36（9）： 7-11. （In Chinese）

[3] NEWMARK N M， SIESS C P， VIEST I M. Tests and analysis of composite beams with incomplete interaction [J]. Society for Experimental Stress Analysis， 1951， 9（1）： 75-92.

[4] GIRHAMMAR U A， GOPU V K. Composite beamcolumns with interlayer slipexact analysis [J]. Journal of Structural Engineering， 1993， 119（4）： 1265-1282.

[5] 聂建国， 沈聚敏， 袁彦声. 钢混凝土简支组合梁变形计算的一般公式[J]. 工程力学， 1994， 11（1）： 21-27.

NIE Jianguo， SHEN Jumin， YUAN Yansheng. A general formula for calculating the deformation of simply supported steelconcrete composite beams [J]. Engineering Mechanics， 1994， 11（1）： 21-27. （In Chinese）

[6] 聂建国， 沈聚敏， 余志武. 考虑滑移效应的钢-混凝土组合梁变形计算的折减刚度法[J]. 土木工程学报， 1995， 28（6）： 11-17.

NIE Jianguo， SHEN Jumin， YU Zhiwu. A reduced stiffness method for calculating deformation of steelconcrete composite beams with the consideration of slip effect [J]. China Civil Engineering Journal， 1995， 28 （6）： 11-17. （In Chinese）

[7] 朱聘儒. 钢-混凝土组合梁设计原理[M]. 北京：中国建筑工业出版社， 2006： 76-96.

ZHU Pinru. Principles of steelconcrete composite beams design [M]. Beijing： China Architecture & Building Press， 2006： 76-96. （In Chinese）

[8] 童根树， 夏骏. 考虑滑移影响的钢-混凝土组合梁的刚度[J]. 建筑钢结构进展， 2008， 10（6）： 1-8.

TONG Genshu， XIA Jun. Bending stiffness of steelconcrete composite beams considering effect of slip [J]. Progress in Steel Building Structures， 2008， 10（6）：1-8. （In Chinese）

[9] GIRHAMMAR U A， PAN D H. Exact static analysis of partially interaction composite beams and beamcolumns [J]. International Journal of Mechanical Sciences， 2007， 49（2）： 239-255.

[10]GIRHAMMAR U A. A simplified analysis method for composite beams with interlayer slip [J]. International Journal of Mechanical Sciences， 2009， 51（7）： 515-530.

[11]蒋丽忠， 余志武， 李佳. 均布荷载作用下钢混凝土组合梁滑移及变形的理论计算[J]. 工程力学， 2003， 20（2）： 133-137.

JIANG Lizhong， YU Zhiwu， LI Jia. Theoretical analysis of interlayer slip and deformation of steelconcrete composite beams under uniformly distributed loads [J].Engineering Mechanics， 2003， 20（2）： 133-137. （In Chinese）

[12]余志武， 蔣丽忠， 李佳. 集中荷载作用下钢混凝土组合梁界面滑移及变形[J]. 土木工程学报， 2003， 36（8）： 1-6.

YU Zhiwu， JIANG Lizhong， LI Jia. Interlayer slip and deformation of steelconcrete composite beams under concentrated loads [J]. China Civil Engineering Journal， 2003， 36（8）： 1-6. （In Chinese）

[13]苗林， 陈德伟. 考虑层间滑移效应的组合梁解析计算[J]. 同济大学学报： 自然科学版， 2011， 39（8）： 1113-1119.

MIAO Lin， CHEN Dewei. Closedform solution of composite beam considering interfacial slip effects [J]. Journal of Tongji University： Natural Science， 2011， 39（8）： 1113-1119. （In Chinese）

[14]胡夏闽， 薛伟， 曹雪娇. 钢-混凝土组合梁挠度计算的附加曲率法[J]. 建筑结构学报， 2010（增刊1）： 385-389.

HU Xiamin， XUE Wei， CAO Xuejiao. The additional curvature method for calculating deflection of steelconcrete composite beams [J]. Journal of Building Structures， 2010（S1）：385-389. （In Chinese）

[15]GB 50017-2003 钢结构设计规范[S]. 北京： 中国计划出版社， 2003： 108-119.

GB 50017-2003 Code for design of steel structures [S].Beijing： China Planning Press， 2003： 108-119. （In Chinese）