台阶式溢洪道摩阻流速沿程变化研究

刘应忠　刘韩生

摘要：为了研究台阶式溢洪道摩阻流速沿程变化规律，将其与相对应的光滑溢洪道进行对比，引入相对摩阻流速的概念。通过对台阶高度为0.5 - 2.0 m、坡角为26.6°- 48.0°、单宽流量为35.7 - 62.2 m/s的台阶式溢洪道模型进行试验，分析了各个模型条件下摩阻流速和相对摩阻流速与流程长度之间的关系。分析发现：台阶式溢洪道摩阻流速沿程变化情况复杂，而台阶式溢洪道相对摩阻流速与流程长度之间具有良好的线性关系，规律显著，便于分析应用，以此论证了引入台阶式溢洪道相对摩阻流速的必要性。适当提高台阶高度对消能有利，在小单宽流量和坡度较陡时，台阶式溢洪道消能效果更佳。

关键词：台阶式溢洪道;摩阻流速;单宽流量;台阶高度;坡度

中图分类号：TV135.2

文献标志码：A

doi：10.3969/j.issn.1000- 1379.2019. 04.023

臺阶式溢洪道是由常规光滑溢洪道发展而来的一种泄水建筑物，是公认的一种高效消能工[1]。摩阻流速是表征河床壁面切应力和研究明渠水流挟沙规律和运动规律的重要参数[2-10]。台阶式溢洪道底部结构比较特别，台阶水流比较复杂，关于其摩阻流速的研究主要集中在常规河渠水流上[11-16].在台阶式溢洪道中研究甚少。Cheng X等[17]利用台阶式溢洪道的断面流速分布计算出了数个水力参数，摩阻流速为其中一个。Chamani M R等[18-19]在研究台阶式溢洪道的流速分布时对摩阻流速有所提及，但并未进行深入研究。笔者基于光滑溢洪道水力计算理论，以试验观测数据为基础，将台阶式溢洪道摩阻流速与相对应的光滑溢洪道摩阻流速进行对比分析，以此引入相对摩阻流速。通过对多组模型试验数据进行处理，分析了台阶式溢洪道摩阻流速和相对摩阻流速在各个模型条件下与流程长度之间的关系，加深了对台阶式溢洪道摩阻流速的认识。

1 相对摩阻流速的定义

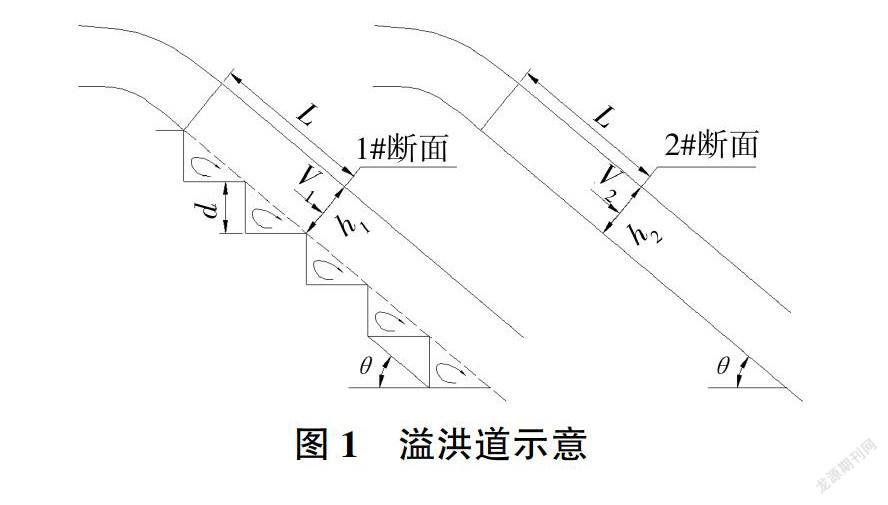
定义光滑溢洪道摩阻流速与对应台阶式溢洪道摩阻流速之差AU8为台阶式溢洪道的相对摩阻流速。本文研究的台阶式溢洪道及与之相对应的光滑溢洪道示意见图1。图1中1#断面和2#断面分别为相对应的台阶式溢洪道断面与光滑溢洪道断面，其中：V1、V2、h，h2：分别为1#、2#断面的平均流速、水深;d为台阶高度：θ为溢洪道坡角江为测点断面位置与起始断面第一级阶梯位置的斜距，即流程长度。

根据定义，任意断面相对摩阻流速为

AU* =U8光一U*台

（1）式中：U*光、U*台分别为光滑溢洪道摩阻流速和对应台阶式溢洪道摩阻流速，m/s。

2 模型试验结果与分析

为探究台阶式溢洪道摩阻流速和相对摩阻流速与流程长度之间的关系，对坡角分别为26. 60、38.70、48.00的台阶式溢洪道进行模型试验，研究了不同台阶高度和不同单宽流量下摩阻流速和相对摩阻流速沿程变化规律。模型试验基本资料见表1。

2.1 摩阻流速、相对摩阻流速与单宽流量的关系

为研究摩阻流速、相对摩阻流速与单宽流量之间的关系，选取单宽流量为35.7、46.7、62.2 m/s，台阶高度为1.0 m，溢洪道坡角为38.70的试验数据进行分析，各流量下的水流均为滑行水流。

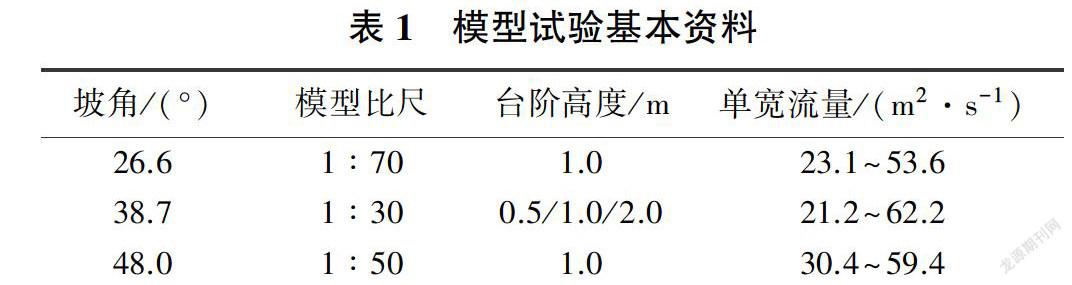
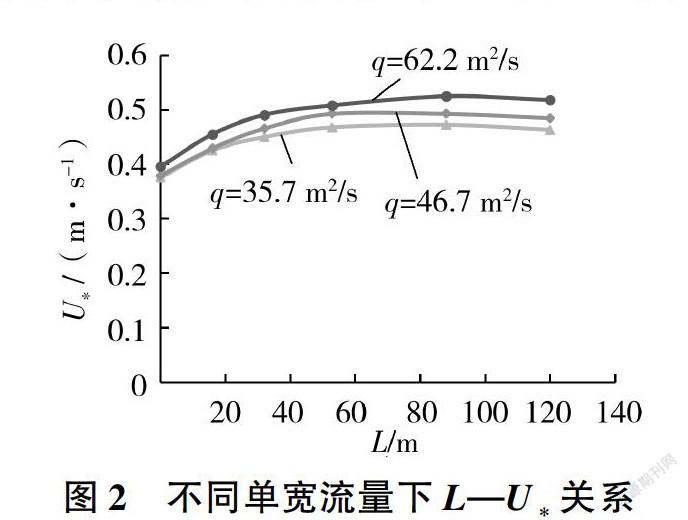
不同单宽流量下，台阶式溢洪道摩阻流速与相对摩阻流速沿程变化规律分别如图2和图3所示。不同单宽流量下台阶式溢洪道摩阻流速在非均匀流段缓慢增大，到达均匀流段后趋于稳定，且摩阻流速随单宽流量的增大而增大。而相对摩阻流速与流程长度之间则有简单且良好的规律，成线性递增关系，线性确定系数R2为0.957 4-0.975 8，其直线斜率随单宽流量的增大而减小，依次为0.005 1、0.005 0、0.004 7，变化很小，表明单宽流量的变化对相对摩阻流速的影响很小，其他工况也符合此规律。基于摩阻流速与平均流速之间为良好的线性关系[20]，结合以上分析可知在提高单宽流量的情况下，台阶式溢洪道摩阻流速虽然逐渐增大，但光滑溢洪道摩阻流速与台阶式溢洪道摩阻流速的差值并没有增大的趋势，而是逐渐减小，这说明增大单宽流量并没有提高台阶式溢洪道相对摩阻流速，即增大单宽流量对台阶消能较为不利。

2.2 摩阻流速、相对摩阻流速与台阶高度的关系

为研究摩阻流速、相对摩阻流速和台阶高度之间的关系，选取台阶高度为0.5、1.0、2.0 m，单宽流量为46.7 m/s.溢洪道坡角为38.70的试验数据进行分析，不同台阶高度下的水流均为滑行水流。

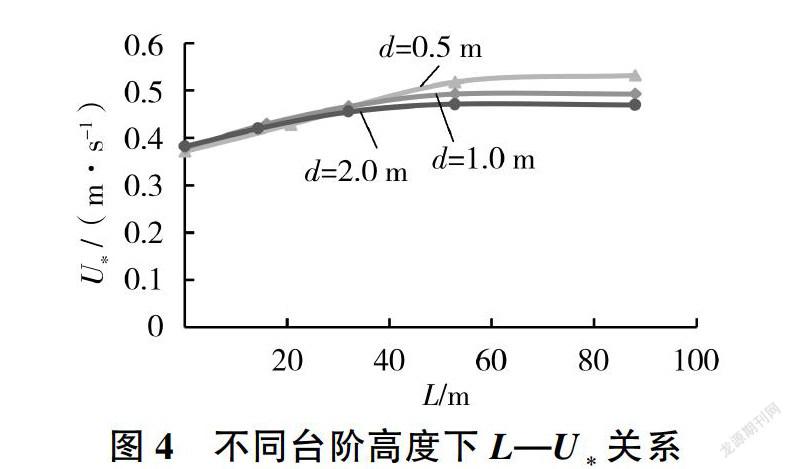
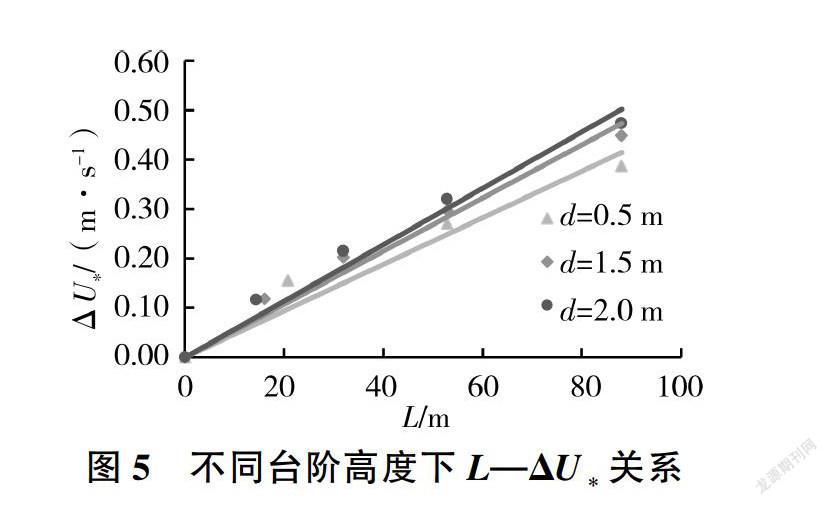
不同台阶高度下，台阶式溢洪道摩阻流速与相对摩阻流速沿程变化情况分别如图4和图5所示。不同台阶高度下台阶式溢洪道摩阻流速在非均匀流段缓慢增大，到达均匀流段后趋于稳定，之后摩阻流速随台阶高度的增大而减小。相比较而言，台阶式溢洪道相对摩阻流速与流程长度之间有良好且简单的线性关系，线性确定系数R2为0.945 6- 0.976 2。与单宽流量变化时不同，其直线斜率随台阶高度的增大而增大，依次为0.004 7、0.005 4、0.005 7，但变化仍然较小。表明在同一条件下，相对摩阻流速随台阶高度的增大而增大，但3条直线的斜率很接近，所以台阶高度对相对摩阻流速影响有限，其他工况也符合此规律。根据以上分析，结合摩阻流速与平均流速之间的关系可知，台阶高度对提高相对摩阻流速有一定的作用，适当提高台阶高度对提高相对摩阻流速有利，即适当提高台阶高度对台阶消能有利。

2.3 摩阻流速、相对摩阻流速与溢洪道坡度的关系

为研究摩阻流速、相对摩阻流速和溢洪道坡度之间的关系，选取溢洪道坡角为26.60、38.70、48.00，单宽流量为35.7 m/s，台阶高度为1.0 m的试验数据进行分析，不同坡角下的水流均为滑行水流。

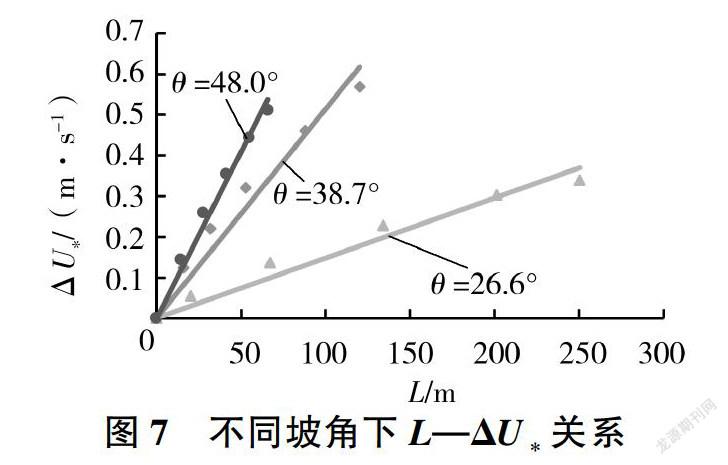
不同溢洪道坡角下，台阶式溢洪道摩阻流速与相对摩阻流速沿程变化情况分别如图6、图7所示。不同溢洪道坡角下台阶式溢洪道摩阻流速沿程变化情况较为复杂，无良好规律。具体体现为：坡角为26.60、38.70时，摩阻流速表现为在非均匀流段缓慢增大，到达均匀流段后趋于稳定，且随坡角的增大而增大：而坡角为48.00时，则呈现为先增大后逐渐减小的趋势。相对摩阻流速与流程长度之间有良好且简单的线性递增关系，线性确定系数R2为0.957 4-0.984 8。其直线斜率随溢洪道坡角的增大而增大，依次为0. 001 5、0.005 1、0.008 2，变化较大。表明相对摩阻流速随溢洪道坡角的增大而增大，且与单宽流量和台阶高度相比，溢洪道坡角对相对摩阻流速的影响比较明显，其他工况也符合此规律。根据以上分析，结合摩阻流速与平均流速之间的关系可知，坡角为26.60 - 48.00时，坡角越大对提高相对摩阻流速的作用越明显，即适当提高坡角可以明显增大台阶结构对水能的损耗。

3 结论

台阶式溢洪道摩阻流速在不同工况下沿程变化情况复杂，无良好的规律，不便分析應用。而台阶式溢洪道相对摩阻流速与流程长度之间为良好的线性关系，线性确定系数R2为0.945 6- 0.984 8，规律简单且良好，便于分析应用。相较于台阶式溢洪道摩阻流速，显然相对摩阻流速沿程变化规律优势明显，以此论证了引入台阶式溢洪道相对摩阻流速的必要性。

台阶式溢洪道相对摩阻流速主要受单宽流量、台阶高度和溢洪道坡角影响，其随单宽流量的增大而减小，随台阶高度、溢洪道坡角的增大而增大，其中受单宽流量和台阶高度影响较小，受溢洪道坡角影响较为显著。表明适当提高台阶高度对提高相对摩阻流速有利，即适当提高台阶高度对消能有利：在小单宽流量和坡角较陡时，台阶式溢洪道消能效果更佳。

参考文献：

[1]艾克明，台阶式泄槽溢洪道的水力特性和设计应用[J].水力发电学报，1998（4）：86-95.

[2] 刘春晶，李丹勋，王兴奎，明渠均匀流的摩阻流速及流速分布[J].水利学报，2005，36（8）：950-955.

[3]张小峰，王冠，明渠非均匀流摩阻流速研究[J].中国水运，2016，16（7）：186-187.

[4] 余江，杨奉广，毋敏，等，含沙波明渠水流摩阻流速模型研究[J].泥沙研究，2014（4）：18-25.

[5] 付辉，杨开林，王涛，等，对数型流速分布公式的参数敏感性及取值[J].水利学报，2013，44（4）：489-494.

[6]PEKIAS A O.Computational Modeling with Sensitivity Analysis：Case Study Velocity Distribution of Natural Rivers [J]. NeuralComputing&Applications，2015，26（7）：1653-1667.

[7] MUSTE M， PATEL V C.Velocity Profiles for Particles andLiquid in Open-Channel Flow with Suspended Sediment[J].Joumal of Hydraulic Engineering， 1997， 123（9）：742-751.

[8] BALACHANDAR R，BLAKELY D，BUGG J.Friction Ve-locity and Power Law Velocity Profile in Smooth and Roughs[J]. Canadian Journal of Civil Engineering， 2002， 29（2）：256-266，

[9]TAN S K，YU G.Errors in the Bed Shear Stress as Estimatedfrom Vertical Velocity Profile[J].Joumal of Irrigation&Drain-age Engineering，2006， 132（5）：490-497.

[10]BERCERON N E，ABRAHAMS A D.Estimating Shear Ve-locity and Roughness Length from Velocity Profiles [J].Water Resources Research， 1992， 28（ 28）：2155-2158.

[11] 张小峰，金栋，卢新华，等，明渠减速流下床面摩阻流速研究[J].华中科技大学学报（自然科学版），2014（ 10）：113-118.

[12] 张红光，路明，范志高，等，明渠渠底糙率突变对紊流摩阻流速及壁面切应力影响的试验分析[J].水利水电技术，2007，38（1）：89-92.

[13]胡江，杨胜发，光滑明渠均匀紊流水流结构研究[J].人民黄河，2009，31（3）：23-25.

[14]王宪业，王协康，刘兴年，等，卵砾石河道摩阻流速计算方法探讨[J].水利水电科技进展，2007，27（5）：14-18.

[15]CHOO T H， SON H S，YUN G S，et al.The Proposal forFriction Velocity Formula at Uniform Flow Channel Usingthe Entropy Concept[J].Journal of the Korea Contents As-sociation， 2015， 15（2）：499-506.

[16]ZHOU T H， GRAF W H.Friction in Unsteady Open-ChannelFlow over Cravel Beds [J]. Joumal of Hydraulic Research，1993， 31（1）：99-110.

[17]CHENC X，GULLIVER J，ZHUD.Application of DisplacementHeight and Surface Roughness Length to DeterminationBoundary layer Development Length over Stepped Spillway[J].Water， 2014， 6（12）：3888-3912.

[18]CHAMAM M R， RAJARATNAM N.Characteristics of Skim-ming Flow over Stepped Spillways [J]. Joumal of HydraulicEngneering， 2000， 125（4）：361-368.

[19]CHENC X J，CULLIVER J S.Velocity Profile for Develo-ping Flow over Stepped Spillway[J].Aip Conference Pro-ceedings， 2011（1）：343-350.

[10]牟明艳，明渠非恒定流摩阻流速与平均流速相互关系初探[D].重庆：重庆交通大学，2016：35-41.