基于谱矩的单自由度复阻尼结构的等效阻尼分析

李暾 谢海文 李创第 葛新广

摘    要：復阻尼模型与实验结果吻合较好，但结构动力分析较为复杂.本文针对单自由度复阻尼耗能结构基于谱矩相等准则，即令复阻尼原始系统和等效系统的的零阶和二阶谱矩相等，得到单自由度复阻尼耗能结构的等效频率和等效阻尼.将等效系统的计算结果与原始系统计算得到的精确解以及由经典的模态应变能法计算得到的结果进行比较，等效系统具有很高的精度.

关键词：复阻尼结构;谱矩;等效频率;等效阻尼;单自由度

中图分类号：TU311.3          DOI：10.16375/j.cnki.cn45-1395/t.2019.04.002

0    引言

复阻尼模型和粘滞阻尼模型是常见的阻尼模型[1-3]，在实际工程中的应用也较为广泛.对于这些阻尼耗能结构，目前在世界范围内进行抗震设防设计基本是基于反应谱的方法进行设计[4-5].地震动特性和阻尼器结构系统的动力特性两者间的关系是抗震设计中的关键问题，这两者之间关系在反应谱中都考虑进去了，因此要用合理的方法确定结构的等效阻尼.

相比于粘滞阻尼，复阻尼模型可以比较好的描述阻尼特性[6-8]，与实验结果相对比，复阻尼模型也比较相符[9].振幅改变、应力等因素对实际应用的材料都有影响，并且材料的能量耗散也与之相关，相比于其他阻尼模型，复阻尼模型考虑到了这些的问题.因此，研究复阻尼耗能结构的地震分析以及其等效阻尼极其具有工程意义.

在对单自由度复阻尼耗能结构动力特性分析方面，已经有对其在频域和时域的研究成果[10-13]，通过对比单自由度复阻尼结构时域精确解法与频域解法之间的情况，分析了在求解过程中一些不恰当的做法，以及在进行时域计算时实部与虚部之间的影响.但大都是采用如精细积分法、Newmark-[β]、平均加速度等方法，尚未解决有关等效阻尼的算法，因反应谱法中需要涉及，本文提供了一种单自由度复阻尼结构的等效阻尼算法.

阻尼耗能结构的解析法分为扩阶法和非扩阶法.对于Maxwell、广义Maxwell模型[14-15]，以及分数导数模型[16-17]，目前一般采用扩阶法，此法可以比较快速获得扩阶的近似模型从而求得结构系统的解析解.但是在应用扩阶法时，常常因其变量个数较多，导致在计算过程中效率降低.经典的模态应变能法[18-19]和强行振型解耦法[20]属于非扩阶法，这两种方法在计算过程中采用了比较多的假设，其适用性和精确性有待提高.

在工程中大量运用的阻尼系统，其动力特性都是由其频率响应函数决定[21].在此基础上，本文重新构造了复阻尼耗能结构的基本分析方程，根据其频率响应函数，基于谱矩相等的等效准则，即原始系统和等效系统的频响函数的各阶谱矩均相等，则两个系统完全等效;如果两个系统有限阶谱矩也相等，则他们近似等效.因此令复阻尼原始系统和等效系统的零阶和二阶谱矩相等，求得单自由度复阻尼耗能结构的近似解析式以及等效阻尼和等效频率.谱矩相等的准则在求解Maxwell阻尼器结构也有应用[22]，用谱矩法求解的优势在于可以直接通过积分的方法求得其各阶谱矩，为在分析其他各种阻尼耗能结构提供一种新思路.

1    复阻尼耗能结构的谱矩分析

复阻尼单自由度系统在地震激励下，其运动方程为[10]：

[mx+k（1+iη）x=-mxg]                                                                          （1）

式中，m——质量;k——刚度;i——虚数单位，i=[-1];[η]——耗损因子，且0<[η]<1;[x]——质点相对于地面位移;[xg]——地震动地面加速度.

方程（1）可以改写为：

[x+ω20（1+iη）x=-xg]                                                                          （2）

式中，

[ω20=km]                                                                                        （3）

方程（2）的频率响应函数为：

[H（iω）=-1（iω）2+ω20（1+iη）]                                                                    （4）

由随机振动结构中的定义，可以得到频率响应函数[H（iω）]的零阶谱矩[I0]和二阶谱矩[I2]表达式分别为：

[I0=-∞+∞ω0H（ω）2dω]                                                                         （5）

[I2=-∞+∞ω2H（ω）2dω]                                                                        （6）

式（5）、式（6）中，[·]表示求模.

将方程（4）代入方程（5）可求得：

[I0=-∞+∞ω0H（ω）2dω=π2ω30η1+1+η21+η2]                                             （7）

同理，将方程（4）代入方程（6）可求得：

[I2=-∞+∞ω2H（ω）2dω=π2ω0η1+η2+1]                                              （8）

2    復阻尼耗能结构的等效系统

2.1   等效系统的谱矩分析

假设结构系统（2）的等效系统为：

[x+2ξeωex+ω2ex=-xg]                                                                        （9）

式中，[ωe、ξe]分别为结构系统待定的等效频率和等效阻尼比（式（9）通常的阻尼结构都可以采用该类等效）.

方程（9）的等效系统的位移频率响应函数[Hxe（iω）]为：

[Hxe（iω）=-1ω2e+2ξeωe（iω）+（iω）2]                                                          （10）

由随机振动谱矩的耗能结构的位移方程，可以求得等效系统的频率响应函数[Hxe（iω）]的零阶谱矩[I0e]和二阶谱矩[I2e]解析式分别为：

[I0e=-∞∞ω0Hxe（iω）2dω=π2ξeω3e]                                                            （11）

[I2e=-∞∞ω2Hxe（iω）2dω=π2ξeωe]                                                            （12）

2.2   基于谱矩的等效频率和等效阻尼比

根据文献[22]，采用谱矩相等的等效准则来求复阻尼的等效频率和等效阻尼，有：

[I0e=I0]                                                                                     （13）

[I2e=I2]                                                                                     （14）

在基于谱矩相等的等效准则下，由式（7）、式（8）以及式（11）、式（12）的关系，可求出复阻尼结构的等效频率和阻尼分别得：

[ω2e=I2eI0e=I2I0=ω201+η2]                                                                  （15）

[ωe=ω0（1+η2）14]                                        &nbsp;                                  （16）

[2ξeωe=πI2e=πI2=2ω0η（1+η2+1）12]                                                         （17）

[ξe=2η2（1+η2+1）12?（1+η2）14]                                                        （18）

3    近似等效系统的精度分析

将用两种近似方法所求得的频率响应函数近似解，即模态应变能法求得的与式（10）和原始方程求得的精确解式（4）进行比较，通过对比分析可得到两种近似方法的计算精度.

3.1   随机响应方差对比分析

对于单自由度复阻尼减震结构的原始方程，在谱密度[Sxg（ω）=S0]的作用下，其位移平稳响应方差为：

[σ2=-∞+∞H（ω）2Sxg（ω）dω]                                                                  （19）

由已经求得的频率响应函数[H（ω）]，可求得原始方程精确解：

[σ2x=πS02ηω301+1+η21+η212]                                                                 （20）

同样由已经求得等效方程的频率响应函数，求得等效方程的解为：

[σ2xe=πS0ηω3e]                                                                                  （21）

由模态应变能法求得的位移平稳响应方差的近似解为：

[σ2x1=πS0ηω31]                                                                                 （22）

3.2&nbsp;  算例分析

对于在工程实际中应用的阻尼耗能结构，实际中绝大多数单自由度基础固定结构自振频率范围为[10 rad/s≤ω0≤30 rad/s].

取下面典型的实际工程参数进行算例分析.

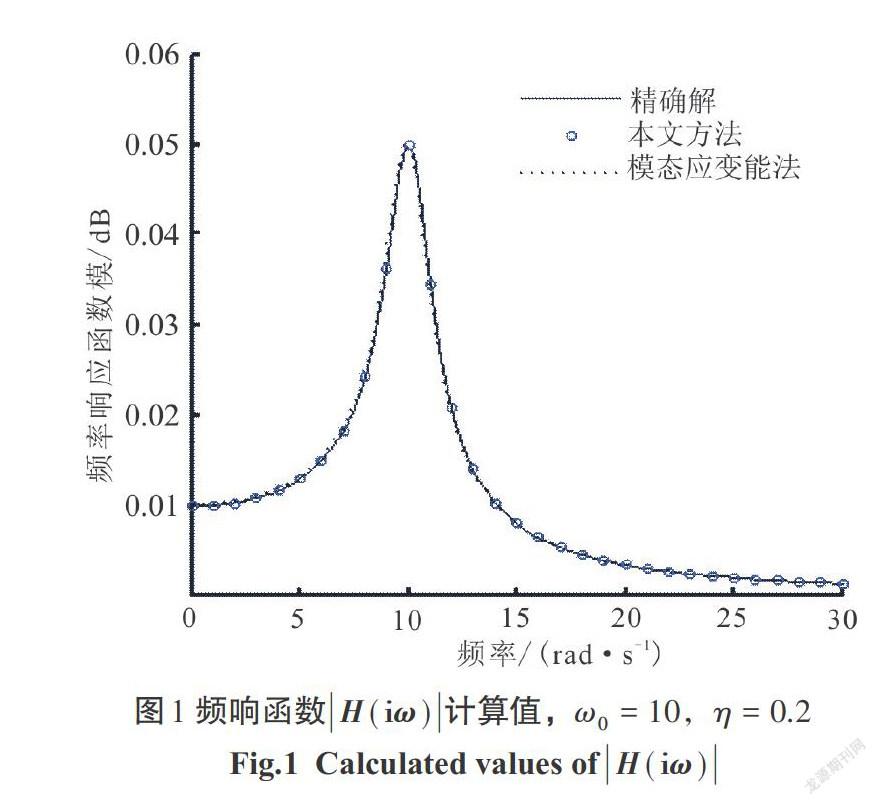
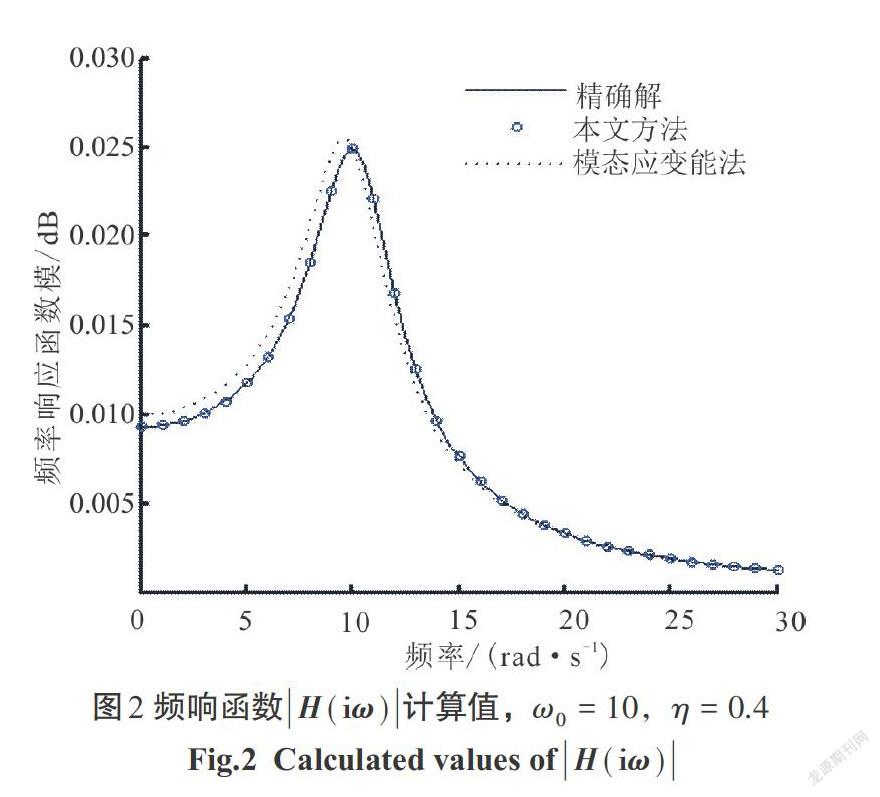
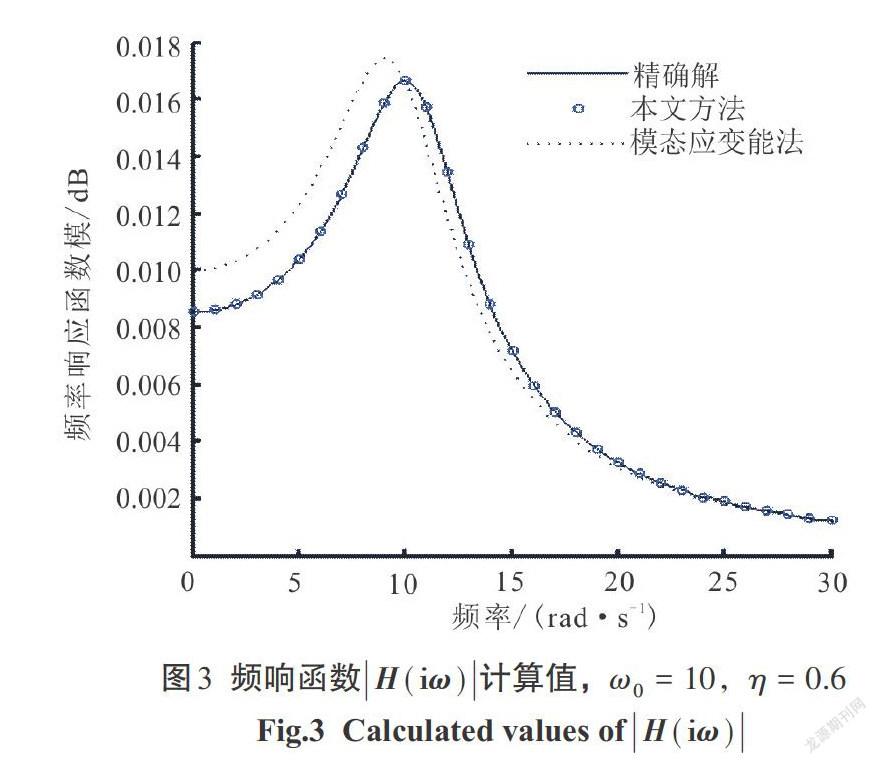
1）自振频率[ω0=10 rad/s]，耗损因子[η]（[0<η<1]）分别取0.2、0.4、0.6、0.8，频率响应函数曲线分别由图1—图4表示.

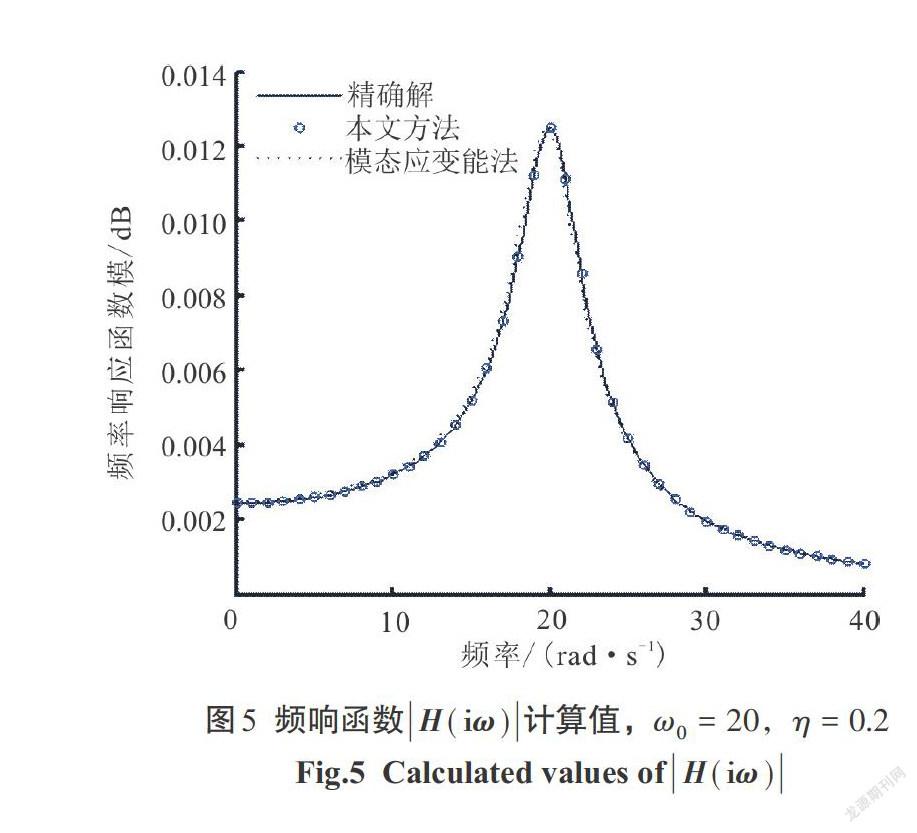
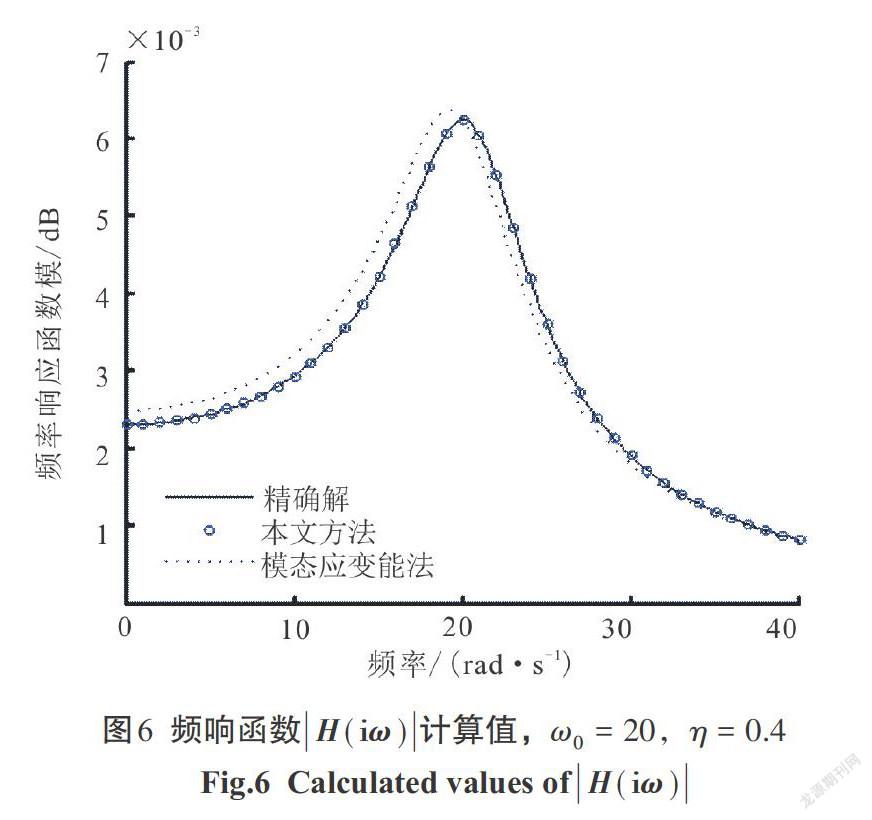
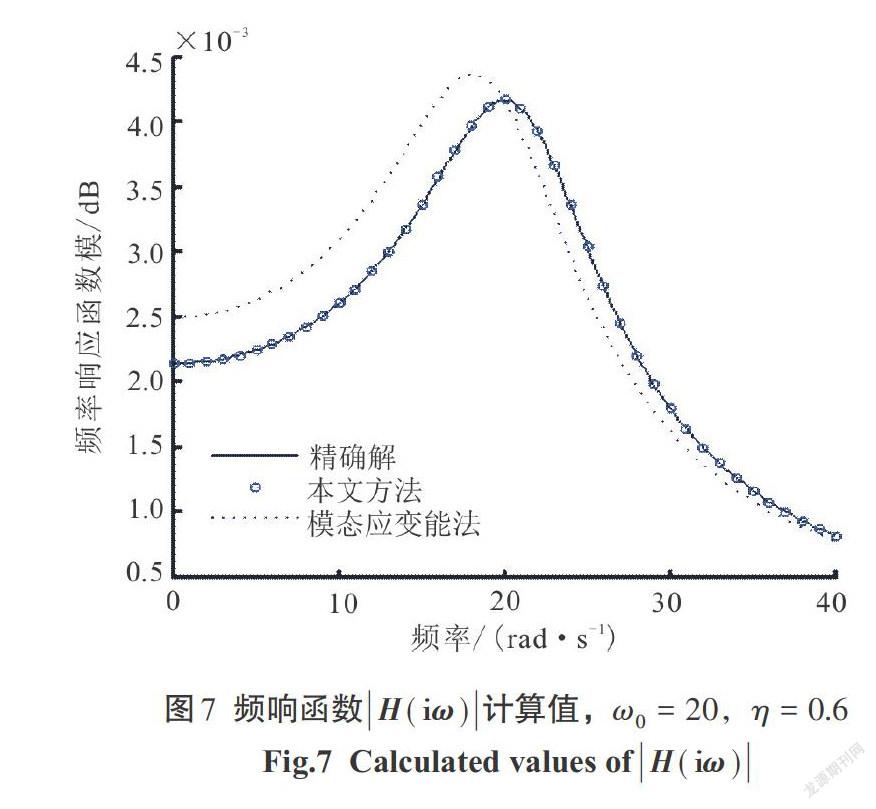
2）自振频率[ω0=20 rad/s]，耗损因子[η]（[0<η<1]）分别取0.2、0.4、0.6、0.8，频率响应函数曲线分别由图5—图8表示.

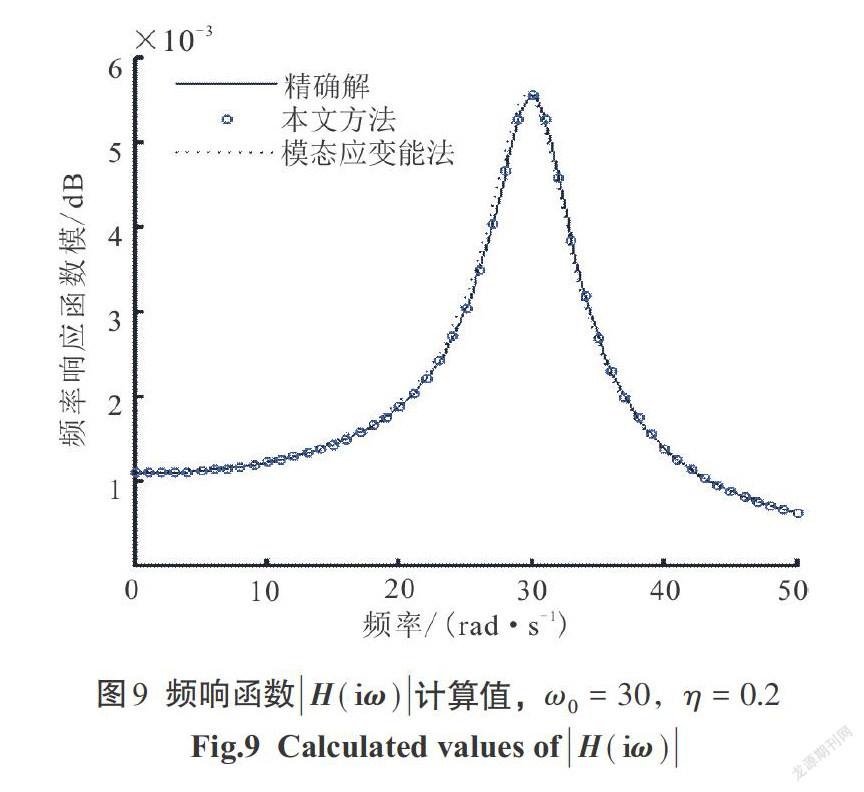
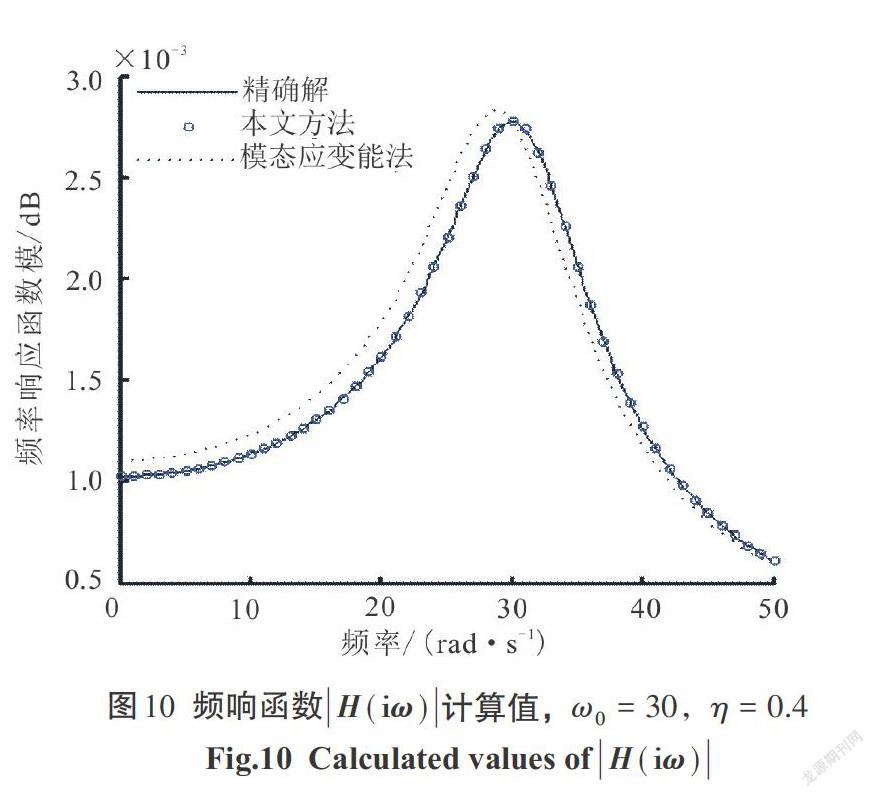
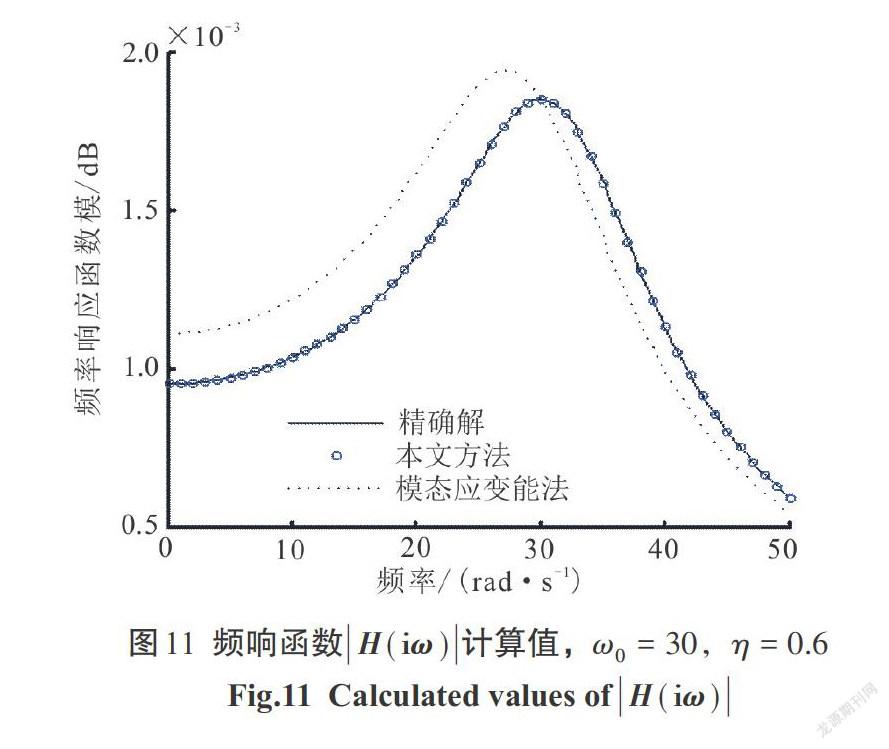
3）自振频率[ω0=30 rad/s]，耗损因子[η]（[0<η<1]）分别取0.2、0.4、0.6、0.8，频率响应函数曲线分别由图9—图12表示.

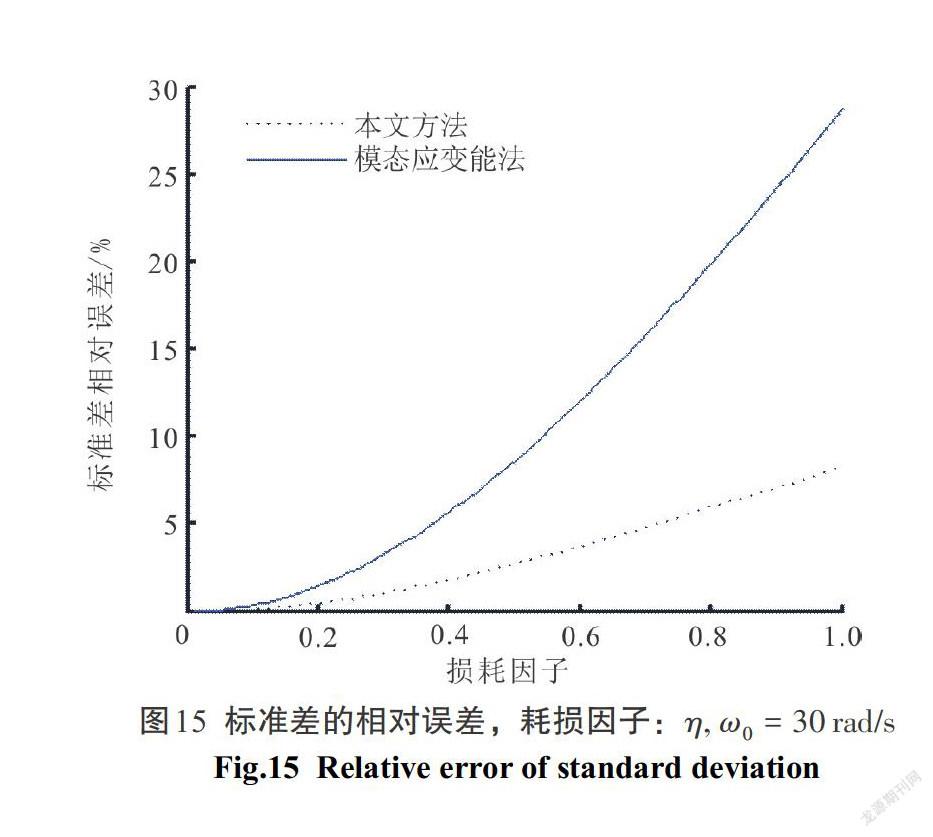
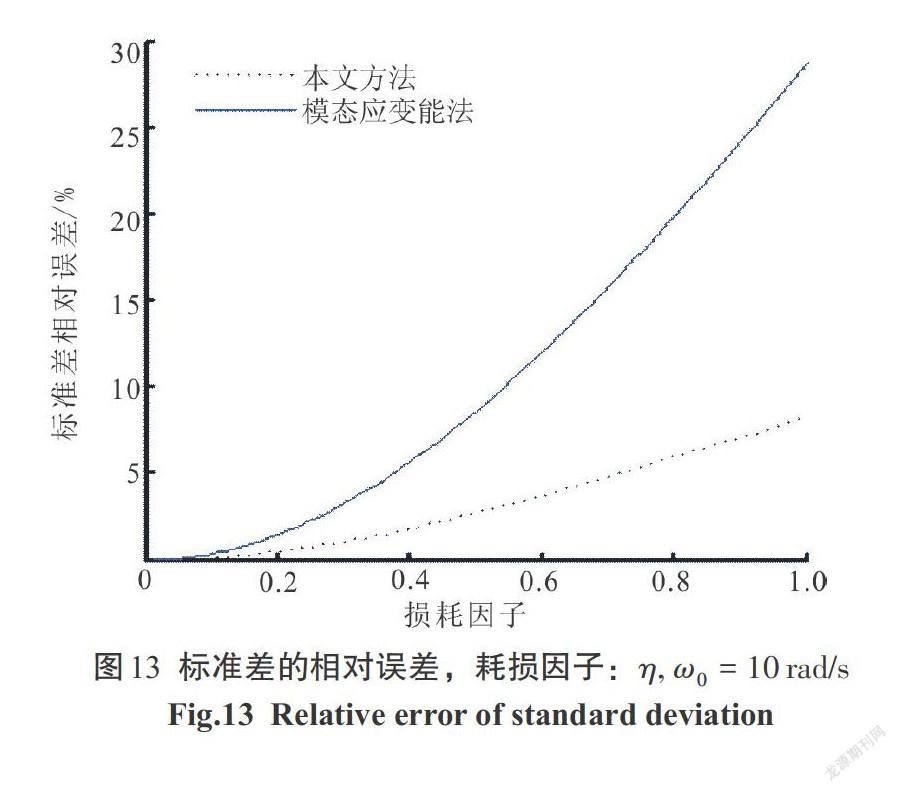
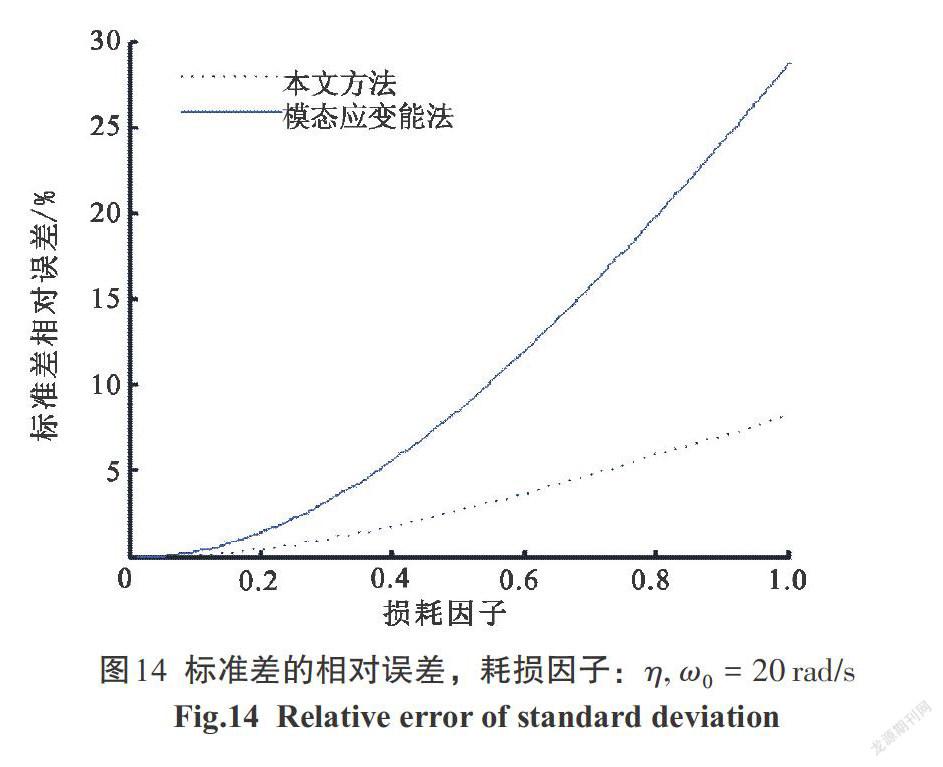
4）图13—图15是当[ω0=10、  20、  30 rad/s]，標准差的相对误差曲线图.

本文方法的标注差的相对误差=[σ2xe-σ2xσ2x]，模态应变能法的标注差的相对误差=[σ2x1-σ2xσ2x].

5）由文献[23]可知，单自由度复阻尼用多尺度法求得的标准差为：

[σxa=πS0ηω20ωa]                                                                             （23）

式中，

[ωa=22ω0（1+1+2η2）12]                                                               （24）

本文方法的标注差的相对误差=[σ2xe-σ2xσ2x]，多尺度法的标注差的相对误差=[σ2xa-σ2xσ2x].

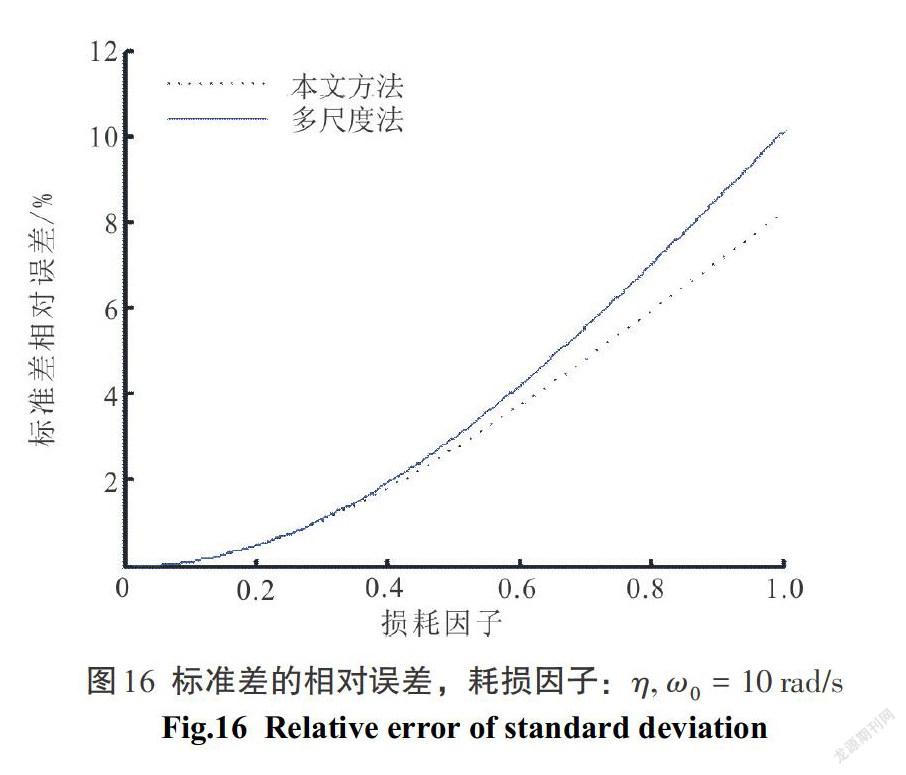
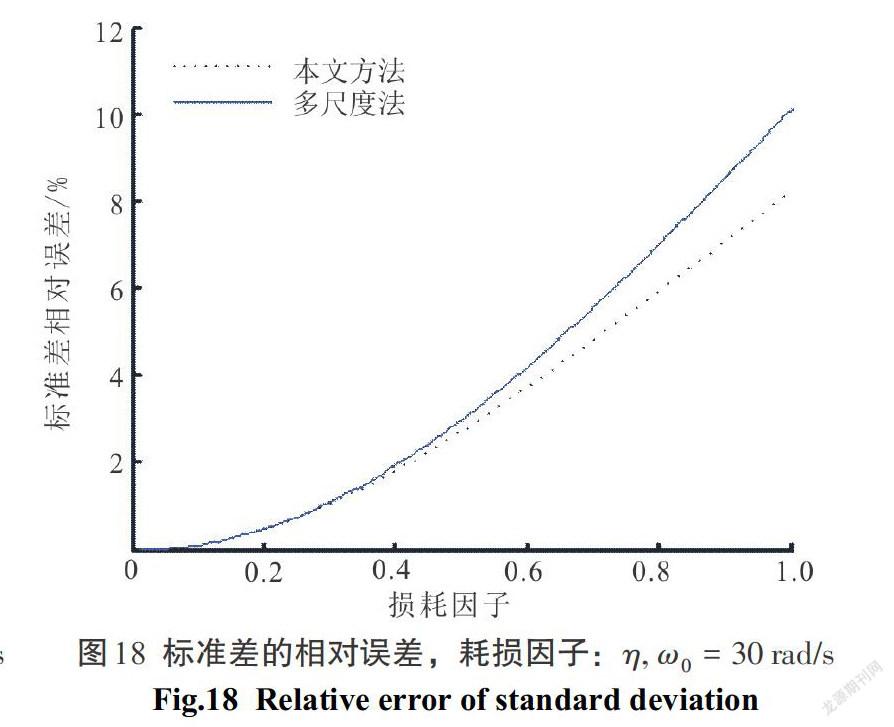
结构图16—图18是当[ω0=10、20、30 rad/s]，标准差的相对误差曲线图.

对于大部分在实际工程中，[ω0]从10 ～30 rad/s为大部分单自由度结构的自振频率范围，以上算例中基本涵盖了此频率范围.

1）图1—图4表明，相对比于用经典的模态应变能法求得的结果，本文用基于谱矩相等准则求得的结果精度更好，且用本文方法求得的等效阻尼与原始方程求得的结果十分接近.

2）对比图1—图12，有：

[①]当耗损因子[η]（[0<η<1]）一定的时候，随着结构自振频率的增大，本文方法较经典的模态应变能法提高的更明显.

[②]当结构自振频率[ω0]一定的时候，随着结构阻尼耗损因子[η]（[0<η<1]）的增大，本文方法较经典的模态应变能法有显著提高，且结构阻尼耗损因子[η]（[0<η<1]）越大，提高越明显.

[③]当处于曲线下降阶段时，已超出我国抗震规范对于参数的要求，因此，在规定范围内本文方法是较优的.

3）图4、图8、图12表明，当结构耗损因子比较大的时候，在规定的范围内本文方法仍优于模态应变能法，说明本文方法对于较大阻尼比的情况仍然适用.

4）图13—图15表明，本文方法对在实际中的单自由度耗能结构[10 rad/s≤ω0≤30 rad/s]，较经典的模态应变能法有很大提高.

5）图16—图18表明，本文方法和多尺度法在实际中的单自由度耗能结构[10 rad/s≤ω0≤30 rad/s].

[①]当耗损因子[η]（[0<η<1]）一定的时候，随着结构自振频率的增大，本文方法比多尺度法精度更好.

[②]由文献[23]知，用多尺度法求得复阻尼结构的等效阻尼精度比经典的模态应变能法已经有很大提高，现对比分析可得，运用本文方法的精度比多尺度法更高.

4    结论

為建立复阻尼耗能减震结构基于反应谱的抗震设计方法，对单自由度复阻尼耗能结构及其等效阻尼和等效频率以及近似解析解进行研究分析，结论如下：

1）单自由度复阻尼耗能结构采用本文方法，求得其等效频率和等效阻尼，解法相对方便，过程也相对简明，因此用本文方法求解，也为其他阻尼耗能结构提供了一种可行的研究分析方法.

2）在采用本文方法下，在抗震设防要求的参数范围内，本文所用的方法优于模态应变能法.通过与多尺度法的求解比较，本文方法所得结果精度比之更高.

3）经过分析可得，绝大部分阻尼相对误差在4%内，对于大阻尼的相对误差也在5%左右，因此大部分实际工程中采用本文方法计算结果都是较好的.

参考文献

[1]     SOONG T T，SPENCE B F.Supplemental energy dissipation：state-of-the-art and state-of-the-practic [J].Engineering Structures，2002，24：243-259.

[2]     李创第，陶欣欣.设置粘弹阻尼器的基础隔震结构平稳响应分析[J].广西科技大学学报，2015，26（2）：20-30.

[3]     中华人民共和国住房与城乡建设部.建筑抗震设计规范：GB 50011—2010[S].北京：中国建筑工业出版社，2016.

[4]     CHRISTOPOULOS C，FILIATRAULT A.Principle of passive supplemental damping and seismic isolation[M]. Pavia，Italy：IUSS Press，2006.

[5]     李创第，李暾，葛新广，等.一般线性粘弹性阻尼器耗能结构瞬态响应的非正交振型叠加精确解[J].工程力学，2015，32（11）：140-149.

[6]     胡海岩.结构阻尼模型及系统时域动响应[J].振动工程学报，1992，5（1）：8-16.

[7]     周正华，廖振鹏，丁海平.一种时域复阻尼本构方程[J].地震工程与工程振动，1999，19（2）：37-44.

[8]     张辉东，王元丰.复阻尼模型结构地震时程响应研究[J].工程力学，2010，27（1）：109-115.

[9]     何钟怡，廖振鹏，王小华.关于复阻尼理论的几点注记[J].地震工程与工程振动，2002，22（1）：1-6.

[10]   朱镜清，朱敏.复阻尼地震反应谱的计算方法及其它[J].地震工程与工程振动，2000，20（2）：19-23.

[11]   丁海平，刘长和.复阻尼理论的一点注记[J].地震工程与工程振动，2001，21（1）：61-63.

[12]   朱镜清，朱敏.复阻尼振动方程频域解法中有关问题的研究[J].世界地震工程，2004，20（1）：23-28.

[13]   孙攀旭，杨红，赵雯桐，等.基于复阻尼模型的时域数值计算方法[J].地震工程与工程振动，2019，39（2）：203-212.

[14]   SINGH M P， CHANG T S. Seismic analysis of structures with viscoelastic dampers[J]. Journal of Engineering Mechanics， 2009，135（6）：571-580.

[15]   ZHANG J，ZHENG G T. The biot model and its application in viscoelastic composite structures[J].Journal of Vibration and Acoustics，2007，129（5）：533-540.

[16]   BAGLEY R L，TORVIK P J.Fractional calculus-a different approach to the analysis of viscoelastically damped structures[J]. AIAA Journal，1983，21（5）：741-748.

[17]   LEWANDOWSKI R，CHORZYCZEWSKI B.Identification of the parameters of the Kelvin-Voigt and the maxwell fractional models used to modeling of viscoelastic dampers[J]. Computers and structures，2010，88（1）： 1-17.

[18]   李宏男.结构振动与控制[M].北京：中国建筑工业出版社，2005.

[19]   JOHNSON C D，KIENHOLZ D A. Finite element prediction of damping in structures with constrained viscoelastic layers[J].AIAAjournal，1982，20（9）：1284-1290.

[20]   OU J P，LONG X，LI Q S.Seismic response analysis of structures with velocity-dependent dampers[J].Journal of Constructional Steel Research，2007，63（5）：628-638.

[21]   李創第，李暾，葛新广，等. 一般线性粘弹性阻尼器耗能结构瞬态响应的非正交振型叠加精确解[J].工程力学，2015，32（11）：140-149.

[22]   李创第，张翊，葛新广.单自由度Maxwell阻尼器耗能结构基于频响函数谱矩的等效阻尼[J].广西大学学报（自然科学版），2019，44（1）：41-51.

[23]   张翊.Maxwell阻尼器与复阻尼耗能减震结构的等效阻尼系统[D].南宁：广西大学，2018.

Equivalent damping of single-degree-of-freedom complex damping structures based on spectral moment

LI Tun， XIE Haiwen， LI Chuangdi*， GE Xinguang

（School of Civil Engineering and Architecture， Guangxi University of Science and Technology，

Liuzhou 545006， China）

Abstract： The complex damping model agrees well with the experimental results， but the structural   dynamic analysis is more complicated. In this paper， the single-degree-of-freedom complex damping  energy dissipation structure is based on the spectral moment equality criterion， that is， the zero-order and second-order spectral moments of the complex damping original system and the equivalent system are equal， and the equivalent frequency and the equivalent damping of the single-degree-of-freedom complex damping energy-consuming structure is obtained. The calculation results of the equivalent   system are compared with the exact solutions calculated by the original system and the results            calculated by the classical modal strain energy method， the equivalent system has high precision.

Key words： complex damped structure; spectral moment; equivalent frequency; equivalent damping; single degree of freedom

（责任编辑：黎   娅）