傅里叶级数构造的装饰图案分析

孙艳玲 姜盈帆 李杰

摘要：在非线性动力系统的计算机可视化研究中，参考Clifford A.Reiter构造“平面结晶体群”的方法，提出截断傅里叶级数构造的平面对称动力系统.分析傅里叶级数的迭代映射的特点，以矩阵乘积的运算形式为工具，构造出非线性函数的截断傅里叶级数对应的平面动力系统.构造出3族截断傅里叶级数的平面对称动力系统，运用蒙特卡罗搜索法选定参数向量，通过李雅普诺夫指数确定动力系统的动力学特性，绘制出3族迭代映射对应动力系统的周期窗口内的混沌图案.提出了一个构造正方形格子平面排列的对称动力系统的方法，采用本文提出的方法可以大量构造正方形平面排列的混沌图案，从而为建筑装饰图案提供了大量的结构新颖、独特别致的素材.

关键词：装饰图案;截断傅里叶级数;周期窗口;充满Julia集

中图分类号：TP391.41  文献标识码：A  文章编号：1673-260X（2019）05-0024-03

混沌动力学和分形几何学是非线性科学的重要组成部分，也是当前科学研究的前沿.20世纪70年代，B.B.Mandelbrot在计算机上构造出了以他的名字命名的Mandelbrot集[1-2]，并创立了分形理论，提出了一种能够用于描述大自然的新几何语言，同时，随着计算机软硬件技术的迅速提高，使得动力系统图形化方面的研究工作得以深入开展.运用混沌、分形理论和计算机图形化研究，可以进一步探索直观生动的可视化图像的证明与构造机制，为发现新现象、研究新规律提供了新的思路.利用分形、混沌等概念大量构造的混沌吸引子图案和各种分形图案的研究工作吸引了从事数学、计算机、艺术设计各个领域研究人员的研究兴趣[3-5]，在这些领域中所取得的研究成果使得人们进一步认识到科学与艺术不可分割的关系.历史告诉我们，新几何学的出现可以成为艺术发展的主要催化剂.由此，分形几何预示着艺术的又一个新的发展.

本文分析傅里叶级数迭代映射的特点，以矩阵乘积的运算形式为工具，利用截断傅里叶级数构造出不同的非线性函数对应的平面对称动力系统.运用蒙特卡罗搜索法选定参数向量，并通过李雅普诺夫指数确定动力系统的动力学特性，构造出周期窗口内的混沌分形图案.从而为建筑装饰图案提供了大批题材新颖、内容生动、形式优美的新图案.

1 截断傅里叶级数

1.1 傅里叶级数的定义

2 截断傅里叶级数构造的装饰图案

2.1 截断傅里叶级数的图形化

文献[6]中提出选取原点附近的固定点为初始迭代点，随机选取一组对应的动力系统的参数，计算对应的李雅普诺夫指数L，并通过挑选使动力系统的L>0的参数构造生成混沌吸引子.但在实际应用中，如果这个固定的初始迭代点不在吸引子的吸引域内，迭代后将不会逼近混沌吸引子，因而不可能用这个固定点得到正确的相应的动力系统的L值.本文采用了一种新的确定初始迭代点的有效方法，即寻找给定参数下的动力系统的Jacobin矩阵行列式值为零的动力平面上的极值点集[7-12]，因此，采用文献[7-12]中的判断动力系统动力学特性的方法随机挑选参数，构造L<0的动力系统的充满Julia集.

2.2 截断傅里叶级数构造的装饰图案

建筑装饰是为保护建筑物的主体结构、完善建筑物的物理性能、使用功能和美化建筑物，采用装饰装修材料或饰物对建筑物的内外表面及空间进行的各种处理过程.装饰图案是指设计者根据用途，对象造型、纹样、材料配置及工艺处理，用图的形式表现的设计理念.装饰图案的合理应用能给建筑及其环境带来无限生机和艺术魅力，给人以美的享受[13].

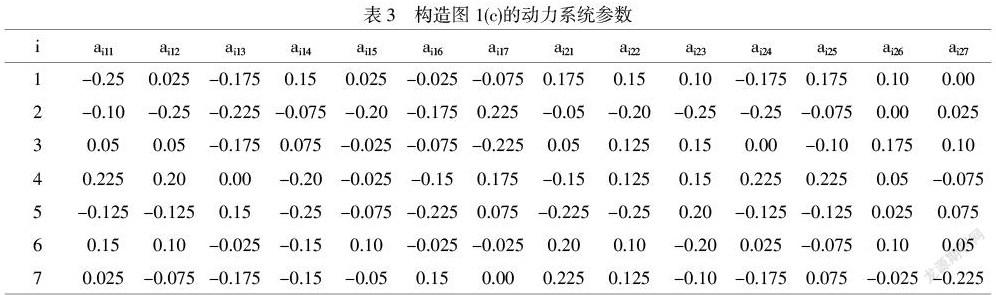
本文将截断傅里叶级数与混沌分形相结合，生成了3族迭代映射对应的平面对称动力系统的充满Julia集图形，直观形象地显示了它们的分形特征.这些奇妙的混沌分形图像不仅具有重要艺术价值，而且可以用于各种需要新颖图案的建筑设计、包装设计、服装设计、装饰布设计、彩色装饰材料设计、纺织印染图案设计、广告设计等等行业，具有广阔的应用前景.图（2）给出了图（1）的3副图在建筑装潢设计中的应用.

3 结论

本文结合文献[3]，同时利用截断傅里叶级数的不同组合形式构造了3族迭代映射.研究3族迭代映射对应的平面对称动力系统的动力学特性，运用蒙特卡罗搜索法随机搜索参数，并通过李雅普诺夫指数确定动力系统的动力学特性，绘制出3族迭代映射对应动力系统的周期窗口内的混沌分形图形.本文提出了一个构造正方形格子平面排列的对称动力系统的方法，采用本文提出的方法可以大量构造正方形平面排列的混沌图案，从而为建筑装饰图案提供了大量的结构新颖、独特别致的素材.

参考文献：

〔1〕Ning Chen， Weiyong Zhu. Bud-sequence conjecture on M fractal image and M-J conjecture between c and z planes from z←zw+c（w=？琢+i？茁）[J].Computers &Graphics，1998， 22（4）：537～546.

〔2〕朱维勇，朱志良，刘向东，等.周期芽胞Fibonacci序列构造M-J混沌分形图谱的一族猜想[J].计算机学报，2003，26（2）：221-226.

〔3〕Carter N C， Eagles R L， et al. .Chaotic attractors with discrete planar symmetries[J]. Chaos Solitions and Fractals， 1998， 9（12）：2031-2054.

〔4〕Lu J，Ye Z X and Zou Y R.Orbit trap tendering methods for generationg artistic images with crystallographic symmetries[J].Computers & Graphics， 2005，29（5）：787-794.

〔5〕Clifford A Reiter.Fractals，Visualization and J 3rd ed. [M].Lulu： Toronto： Jsoftware， Inc.， 2007.

〔6〕Sprott J C. Automatic generation of strange attractors [J]. Computers & Graphics， 1993， 17（3）：25-32.

〔7〕Sun Yan-Ling，Zheng Li and Hou Jing.Construction of Planar Dynamic Systems with Function of Non-linear Angle Variables[J].Applied Mechanics and Mechatronics Automation，2012：1590-1595.

〔8〕Chen N， Sun J， Sun Y L， et al..Visualizing the complex dynamics of  families of polynomials[J].Chaos， Solitons & Fractals， 2009， 42（3）：1611-1622.

〔9〕陳宁，孙艳玲，孙晶.构造变基本域的P1平面对称动力系统[J].沈阳建筑大学学报：自然科学版，2008，24（6）：1099-1102.

〔10〕陈宁，孙晶，孙艳玲.构造具有Zn-1对称的复动力系统[J]. 沈阳建筑大学学报（自然科学版），2008，24（5）： 890-894+928.

〔11〕孙艳玲，陈宁.构造新结晶体群的平面对称动力系统[J].科技广场，2010（1）：49-50.

〔12〕陈宁，孙艳玲，孙晶.变周期窗口平面动力系统的构造与可视化[J].计算机辅助设计与图形学学报，2010，22（5）：784-790.

〔13〕周慧.室外建筑与景观中装饰图案的应用[J].艺术与设计（理论），2008（5）：80-82.