完全分布式无线传感网中的声源定位与跟踪
2019-09-10冯玉武胡国华洪蕾
冯玉武 胡国华 洪蕾


摘要:无线传感网中的每个传感器节点用于无线通信与计算的能量都是有限的.因此,如何有效地减少传感器节点的能量消耗是一个值得研究的问题.为了大幅度减少能量消耗,在本篇文章中,提出了完全分布式EM算法用于无线传感网中的声源定位与跟踪.此算法仅需局部的数据传输与简单的计算.每个传感器节点仅需将其检测到的能量值传输到其单跳范围内的邻居节点,同样也会接收来自单跳范围内的邻居节点检测到的数据,这样就有效地避免了远距离的无线传输,达到大量减少能量消耗的目的.完全分布式EM算法在定位精度与能量消耗方面提供了一个很好的折中,有关静态声源定位与动态声源跟踪的大量仿真实验验证了此算法的可行性.
关键词:声源定位;完全分布式EM算法;无线传感网;能量消耗
中图分类号:TN913.2 文献标识码:A 文章编号:1673-260X(2019)06-0043-04
1 引言
在传感器监测区域内,无线传感网能够实现多项任务的监测[1,2],比如探测、分类、定位以及单目标或多目标的跟踪等.在诸多的无线传感网的应用中,声源定位[3]具有广泛的应用前景,也是吸引了众多科研工作者的关注.如今大多数的声源定位方法根据传感器节点采集的物理量可分为三类:基于DOA(direction of arrival)的声源定位,基于TDOA(time difference of arrival)的声源定位和基于RSS(received signal strength)的声源定位.基于DOA的声源定位算法中,对于硬件的要求相对较严格,同时计算的复杂度也较高;基于TDOA的声源定位算法中,对时钟的同步要求比较高,而精准的时钟同步在无线传感网中又很难实现,因此对于能量受限的无线传感网来说,定位精度高、能量消耗少的基于RSS的声源定位算法[4,5]是比较适合的.
近年来,一些基于RSS的声源定位算法相继被提出.Sheng[6]等人提出应用极大似然估计的方法解决无线传感网中的声源定位问题,对于似然函数方程有两种求解方法,分别是M-R算法与EM算法,这两种算法都需要有大量的远距离数据传输,进而需要消耗大量能量,而这并不适合能量受限的无线传感网.
在集中式EM算法的基础上[7],本篇文章提出了较有创新的完全分布式EM算法实现声源定位与跟踪,在保证定位精度的同时尽量减少能量的消耗.在完全分布式EM算法中,大量的原始数据不需要远距离传输,局部的数据传输与计算就可以完成声源位置的估计.
2 信号衰减模型
假设N个传感器节点布置在一个二维的区域中,且传感器节点的位置已知,表示为ri=[xi,yi]T,i=1,2,…,N,上標T表示向量的转置,在某个时间点k,一个声源正在发射声音信号,声源的位置表示为rs(k)=[xs(k),ys(k)]T,则第i个传感器节点接收到的信号能量强度可表示为[7]:
3 完全分布式EM算法
3.1 分布式计算
在集中式算法中,所有传感器节点都需要通过远距离的无线传输将检测值传输到汇聚节点,这往往需要消耗节点的很大一部分能量,然而在分布式算法中[8],仅需要局部的数据传输与处理就可以完成声源位置的估计,这大大减少了远距离数据传输所带来的能量消耗[9].
本篇文章中,我们提出了完全分布式EM算法,在完全分布式EM算法中,每个传感器节点仅需将其检测到的能量值传输到其单跳范围内的邻居节点,同样也会接收来自单跳范围内的其他邻居节点检测到的数据,每个传感器节点都将根据这些检测值完成声源位置的局部估计,最终再根据所有节点的局部估计值求一个简单的平均值进而得到最终的声源位置估计值.完全分布式EM算法主要包括以下3个部分:
1)第i个传感器节点将检测到的能量值传送给单跳范围内的其他节点,即集合Ωi中的传感器节点,同时也将接收来自单跳范围内其他节点的检测值;
2)根据第i个传感器节点接收到的检测值{yi}∪{yim,m∈Ωi},利用高效的EM算法进行计算,求得声源位置的局部估计值si;
3)每个传感器节点的估计值,包括{si,i=1,2,…,N},最后都路由到汇聚节点,汇聚节点通过简单的求均值的方法即可得到最终声源位置的估计值.
3.2 完全分布式EM算法
在EM算法中,假设把单位距离处的能量强度 作为隐变量,对(4)式求偏导,即∂ℓi/∂S=0可得:
在EM算法的M步,为了求得公式(9)的最优解,本篇文章采用了β变量搜寻算法[7].此种算法的主要思想就是不断地去调整搜寻区域.在首次迭代过程中,选取了较大的搜寻区域以便能够得到全局解,然后慢慢地逐渐缩减搜寻区域,逐次迭代,以此来提高定位精度.通过EM算法收敛特性的分析,可以得到每次迭代的步长.相比多分辨率搜索算法,β变量搜寻算法具有较低的计算复杂度和较高的定位精度.
4 仿真实验
4.1 单声源定位
在一个100m×100m的二维监测区域内,假设有一声源在此区域的任意地点处发出声音信号,声音信号在单位距离1m处的能量强度为500,同时假设有N个传感器节点随机散布在监测区域内,传感器节点的增益相同且为1,对于每个传感器节点而言,在接收信号的过程中受到的噪声影响均假设为高斯白噪声,μ=1,σ=0.1,在单位时间内采样点数为100,传感器节点的单跳距离为50m.
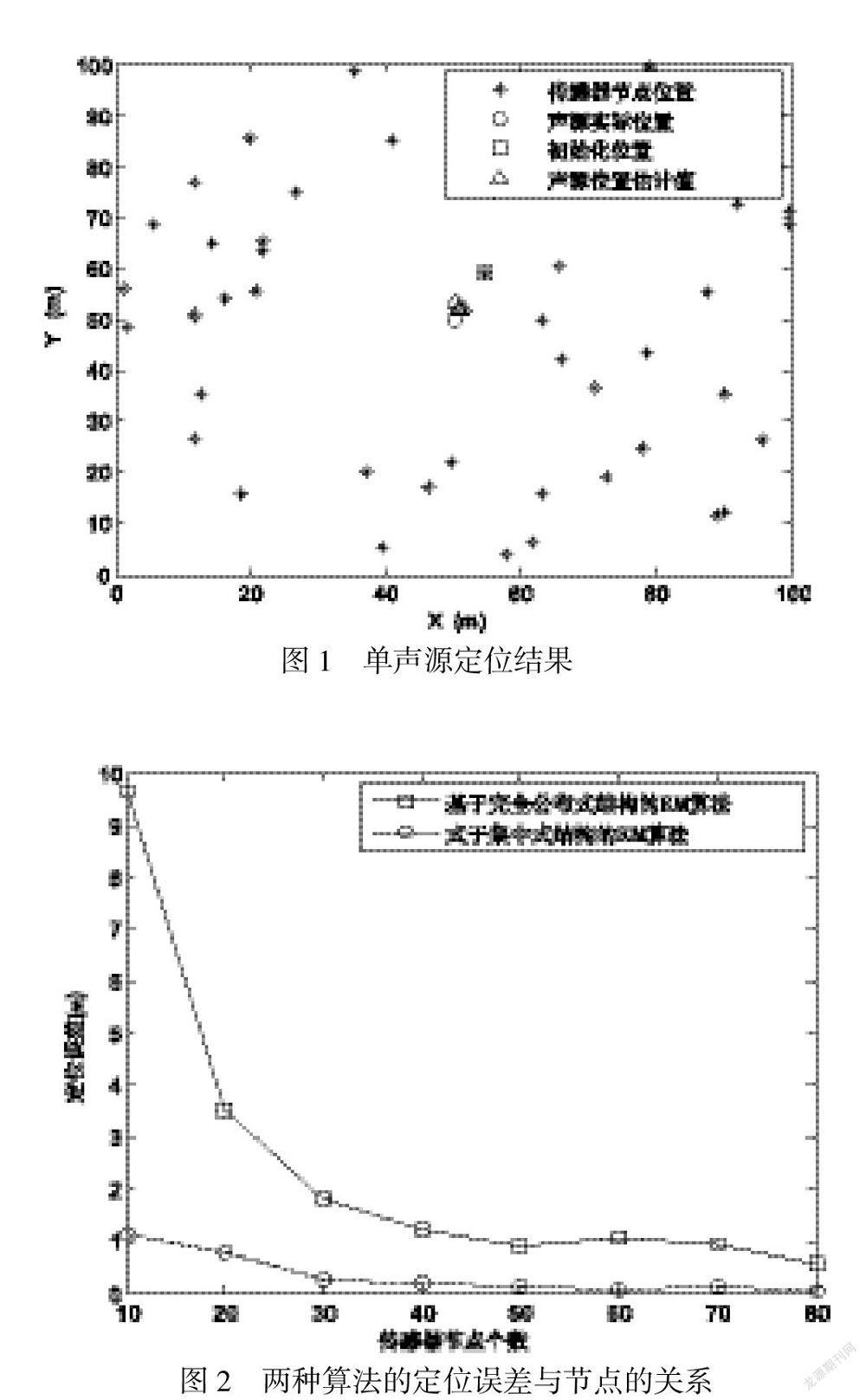
本篇文章所提出的完全分布式EM算法的定位结果如图1所示,监测区域内共布设了50个传感器节点,从图1中可以看出,估计出的声源位置非常接近声源的真实位置,因此仿真实验验证了完全分布式EM算法具有较高的定位精度.
均方根误差(RMSE)是衡量声源定位精度高低的重要指标之一,本篇文章也采用RMSE来对比两种算法的定位精度.为了更加有效的比较完全分布式EM算法与集中式EM算法的定位精度,两种算法的最大化求解步骤均采用β变量搜寻算法.从图2可以看出,随着布设传感器节点个数的增加,完全分布式EM算法的定位精度也在逐渐提高,在传感器节点个数达到80个时,完全分布式EM算法的定位精度非常接近集中式EM算法的定位精度,但是完全分布式EM算法有效地避免了大量数据的远距离无线传输,节省了大量能量,接下来详细分析能量的相关消耗.
4.2 能量消耗分析
相距为d的两个传感器节点间传输p比特的数据时,所需消耗的能量可以通过下面的表达式定量分析[10,11]:
E(p,d)=Eelec×p+εamp×p×d2,(d<d0)
Eelec×p+εamp×p×d4,(d≥d0) (11)
其中Eelec=50nJ/bit表示无线电装置启动电路所需要消耗的能量,εamp=100pJ/bit/m2表示传输放大器启动电路所需要消耗的能量,d0表示距离的阈值.
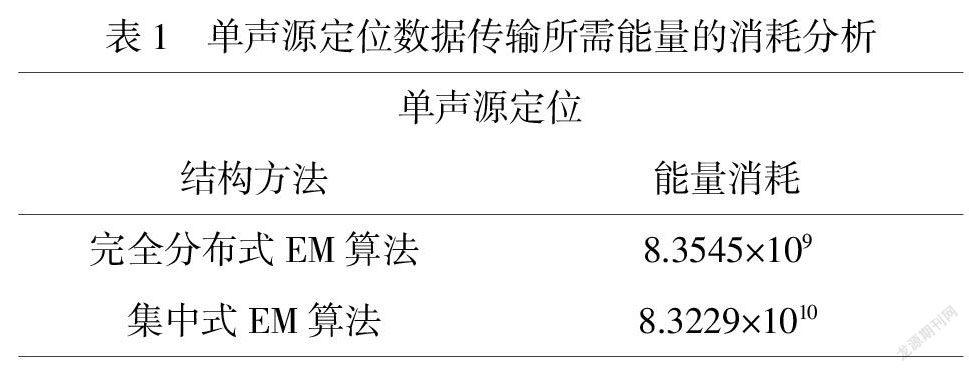
由公式(11)可知,远距离无线传输数据需要消耗很多的能量,特别是当两个传感器间的距离大于阈值的情况.在完全分布式EM算法中,传感器节点仅在单跳范围内进行数据传输,大大缩减了传输距离,进而减少能量的消耗.为了比较方便,在仿真实验中设Eelec==1,p=10,εamp=1,单跳距离设为d0=50m,传感器节点个数设为N=50,通常情况下汇聚节点设置在监测区域外,假设为(110,110)处,对此进行了实验仿真,数据如下表1:
由表1可知,完全分布式EM算法节省了大量能量,同时从图2与表1可知,完全分布式EM算法在定位精度较高的同时节省了大量能量,对于能量有限的无线传感器网络来说是一个合适的选择.
4.3 动态声源跟踪
本篇文章中第二种场景考虑的是一个动态声源的跟踪,在6.28分钟内,一个动态声源留下了圆形轨迹,仿真实验中在监测区域内布设80个传感器节点,其他的条件与4.1节单声源定位相同.
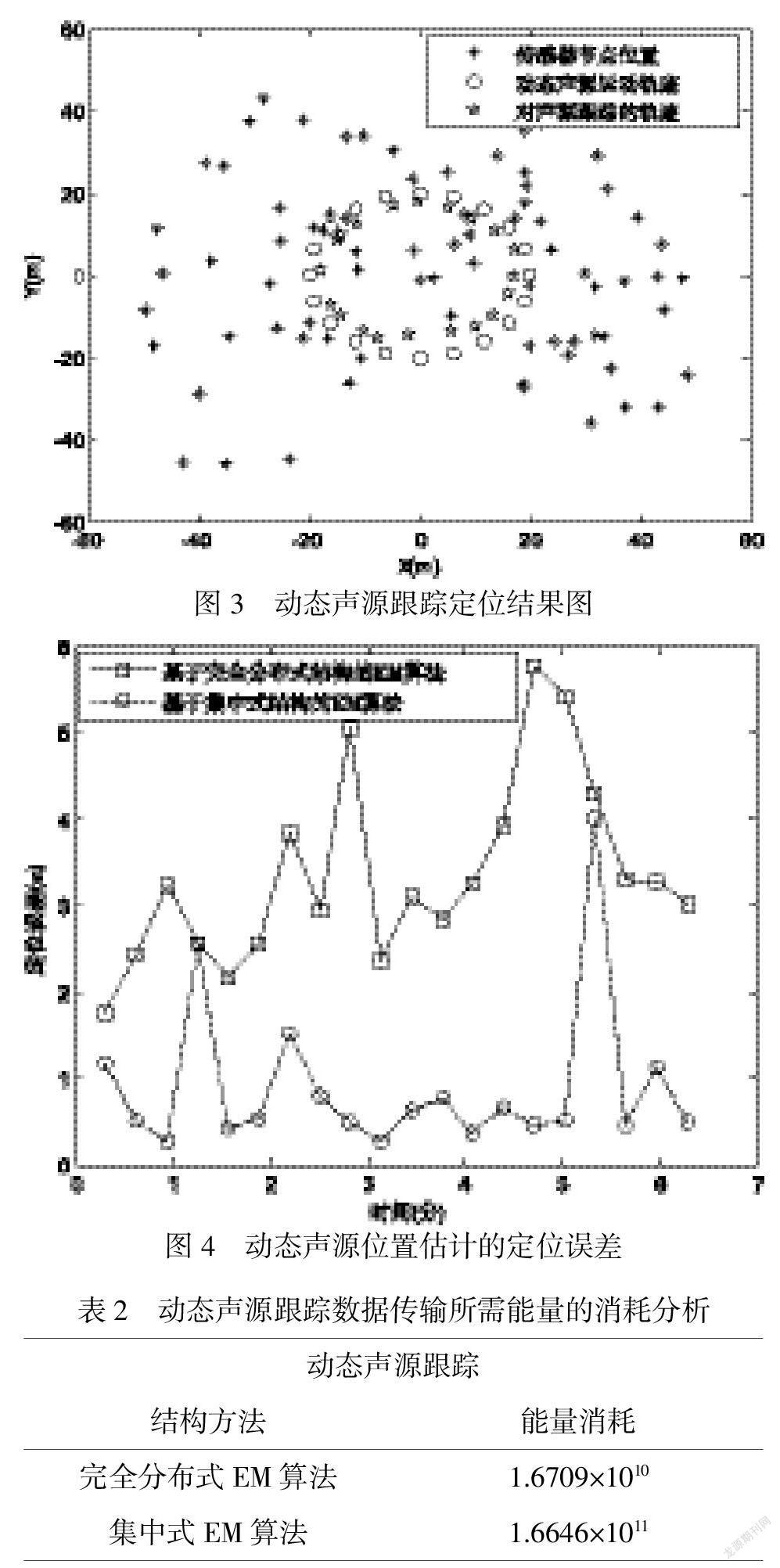
本篇文章所提出的完全分布式EM算法的定位结果如图3所示,从图中可以看出,完全分布式EM算法的定位结果已经非常接近动态声源的運动轨迹,较好地完成了对动态声源运动轨迹的跟踪.
同样的,集中式EM算法与完全分布式EM算法对动态声源位置估计的均方根误差同传感器个数之间的关系图如图4所示,同时结合表2可以看出,当定位结果在可接受的定位精度范围内,较集中式EM算法相比,完全分布式EM算法有效地避免了大量数据的远距离无线传输,节省了大量能量.
5 总结
针对无线传感网中的单声源定位及动态声源的跟踪问题,本篇文章提出了完全分布式EM算法.此算法能够在保证定位精度的基础上,有效地避免了大量数据的远距离无线传输,节省大量能量.仿真实验验证了完全分布式EM算法能够在定位精度与能量消耗之间做一个较好的折中,完全分布式EM算法的定位精度略低于集中式EM算法,但却节省了大量能量.后续将继续展开多声源的定位研究.
参考文献:
〔1〕Holger K. and Andreas W.,无线传感器网络协议与体系结构[M].北京:电子工业出版社,2007.
〔2〕Li D, Wong K D, Hu Y H. Detection, classification, and tracking of targets[J]. IEEE signal processing magazine, 2002, 19(2): 17-29.
〔3〕邵怀宗,林静然,彭启琼.基于麦克风阵列的声源定位技术研究[J].云南民族大学学报,2004(10):1-14.
〔4〕何风行,余志军.基于RSS的WSN多目标定位压缩感知算法优化[J].南京邮电大学学报,2012(8):24-28.
〔5〕Sheng X, Hu Y H. Energy based acoustic source localization[C]. Information Processing in Sensor Networks. Springer, Berlin, Heidelberg, 2003: 285-300.
〔6〕Sheng X, Hu Y H. Maximum likelihood multiple-source localization using acoustic energy measurements with wireless sensor networks[J]. IEEE Transactions on Signal Processing, 2005, 53(1): 44-53.
〔7〕Meng W, Xiao W, Xie L. An efficient EM algorithm for energy-based multisource localization in wireless sensor networks[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(3): 1017-1027.
〔8〕Liu Y, Hu Y H, Pan Q. Distributed, robust acoustic source localization in a wireless sensor network[J]. IEEE Transactions on signal processing, 2012, 60(8): 4350-4359.
〔9〕Feng Y, Huang Q. Fully distributed acoustic source localization in wireless sensor network[C]. TENCON 2013 IEEE Region 10 Conference (31194). IEEE, 2013: 1-4.
〔10〕Heinzelman W R, Chandrakasan A, Balakrishnan H. Energy-efficient communication protocol for wireless microsensor networks[C]. System sciences, 2000. Proceedings of the 33rd annual Hawaii international conference on. IEEE, 2000: 10 pp. vol. 2.
〔11〕Heinzelman W B, Chandrakasan A P, Balakrishnan H. An application-specific protocol architecture for wireless microsensor networks[J]. IEEE Transactions on wireless communications, 2002, 1(4): 660-670.
