基于时间序列方法建立广东省肺结核病发病预测模型

曾洁文

摘要：以广东省2004-2016年各月肺结核发病例数为数据基础，结合时间序列分析方法与SAS软件、Excel软件，构建广东省肺结核发病例数预测模型疏系数ARIMA（（11，12），1，（1，11））模型，得出广东省肺结核发病规律为每年的3月-8月是广东省肺结核发病的高发期，4月、12月分别为每年发病的最高峰和最低峰.用2017年各月肺结核发病例数检测模型预测效果，预测值符合广东省肺结核发病规律，平均绝对百分比误差为2.12%，模型属于高精度模型.对2018年各月肺结核发病例数进行预测，预测值均落入95%置信区间内.疏系数ARIMA（（11，12），1，（1，11））模型可较精确预测广东省肺结核发病例数，为肺结核的预防控制工作提供理论基础.

关键词：时间序列;疏系数ARIMA模型;肺结核;预测

中图分类号：O213  文献标识码：A  文章编号：1673-260X（2019）06-0011-03

肺结核是一种由结核分枝杆菌入侵人体分布而引起的慢性传染病.肺结核虽然是乙类传染病，但在传染性疾病中排名第一.虽然结核病的防控在中国已经取得了很大的进步，但现今中国仍然是肺结核流行病的重灾区，其严重程度仅次于印度和印度尼西亚，而广东省又是我国肺结核负担最重的省份.广东省我国的流动人口大省，人口相对我国其他省份高度集中，再加上肺结核是呼吸道传染病，以上条件为肺结核在广东省的传染和爆发提供了基础.刘维华、朱建良、郭付爱等已为石家庄地区建立学校结核病预警模型[1];李晓荣、庞学文、于燕明等人已对天津市结核病发病建立ARIMA（0，1，1）（0，1，1）模型进行预测[2].然而至今尚缺乏针对广东省肺结核发病的、有效的模型拟合并预测.本研究结合时间序列理论，以广东省2004年1月—2016年12月广东省肺结核发病例数为建立模型的数据基础，建立疏系数求和自回归移动平均模型，即疏系数ARIMA模型，预测广东省未来各月肺结核发病情况，为广东省及时采取有效且迅速措施提供重要理论依据，同时为其他省份建立肺结核发病预测模型提供方法与基础.

1 资料和方法

1.1 数据来源

数据来源是中国疾病预防控制中心官网中广东地区2004年-2018年各月肺结核发病例数.

1.2 研究方法

1.2.1 疏系数ARIMA模型理论基础

ARIMA模型，即求和自回归移动平均模型，是由美国统计学家Box和英国统计学家Jenkins与1970年提出的经典时间序列分析模型，主要运用于单变量、同方差场合下.该模型的基本思想是某件事情的发展通常是有一定惯性的，即时间序列值之间的相关关系，而该相关关系又具有某种统计性质或规律，当这种统计规律被刻画描述出来后，就可以对时间序列的历史值和当前值进行拟合、对未来值进行预测.而疏系数ARIMA模型是指原ARIMA（p，d，q）模型中的自相关系数和移动平均系数有部分缺省的模型，ARIMA（（p1，p2…pm）），d，（q1，q2…qn）.[3]

1.2.2 疏系数ARIMA模型建模方法

以广东省2004年1月—2016年12月广东省肺结核发病例数为建立模型的数据基础.第一步，观察初始序列图，获取初始序列的基本、明显特征，进行平稳性检验，根据自相关系数函数与偏自相关系数函数判断初始序列是否具有周期性和趋势性，并确定周期长度和趋势走向.第二步，根据第一步中获取的初始序列特征，对初始序列进行合适的差分∇d与周期差分∇s，消除初始序列的非平稳性，并再次进行平稳性检验，获得平稳时间序列.第三步，根据差分后序列的自相关函数与偏自相关函数，为初始疏系数ARIMA模型定阶.第四步，在初始模型基础上调整参数并对参数进行最小二乘估计与最大似然估计，直至各个参数均通过显著性检验、差分后序列通过白噪声检验与残差自相关检验.最后，在最终模型的基础上，利用广东省2017年1月—12月的肺结核发病例数对模型预测做出评价，对2018年1月—12月的肺结核发病例数做出预测和95%的置信区间.

1.3 统计分析工具及水平

本研究中采用SAS软件和Excel软件进行分析，显著性水平取0.05.

2 模型建立過程

2.1 获取序列特征

从Excel软件制作的广东省2004年1月-2016年12月肺结核发病例数时序图可知，广东省2004-2016年各月肺结核发病例数总体呈现波动性的先上升后下降的趋势，且有明显的周期性，周期长度为12个月.

为了提取出广东省肺结核发病的具体规律，本研究采用提取季节指数的方法提取广东省肺结核发病规律，计算广东省2004-2016年同年各月肺结核发病总月平均例数，以及13年间的总平均发病例数，将同年各月总平均发病例数除以13年间总平均发病例数，算得各月季节指数分别为：1.15、0.94、1.17、1.21、1.19、1.14、1.12、1.11、1.02、1.02、0.87、0.71.其中，4月的季节指数最高，为1.21;而12月的季节指数最低，为0.71.3月到8月的季节指数持续偏高，9月开始有明显下降趋势，最低降至12月，在下一年的1月又有回弹并重复前面的规律.

从季节指数计算结果可知，广东省肺结核发病规律为：每年的4月是全年发病例数最高峰，3月—8月是肺结核病的高发期，从9月开始广东省肺结核发病例数较3月-8月有明显持续性下降，至11月、12月肺结核病发病危险程度已降至较低水平，12月是全年发病例数最低谷.

2.2 疏系数ARIMA模型定阶

2.1节中已知广东省2004年1月—2016年12月肺结核发病例数时序有一定的趋势性和明显的周期性，周期长度为12个月，所以初始序列属于非平稳序列，要对序列进行1阶12步差分.差分后的序列在0.05的显著性水平上通过单位根检验且不能通过白噪声检验，则可认为差分后序列是平稳的非白噪声序列，需要继续提取信息.利用SAS软件做出差分后序列的自相关（ACF）图和偏自相关（PACF）图，可知自相关系数除了在延迟11、12阶时明显超出了2倍标准差，在1阶之后基本上落在2倍标准差以内;而偏自相关系数除了在延迟11、12、24阶的时候明显超出2倍标准差，在3阶之后基本落在2倍标准差以内.综合考虑自相关系数与偏自相关系数的情况，建立初始疏系数ARIMA（（1，2，11，12）1，（2，3，11，12））.

由于在参数显著性检验中初始疏系数ARIMA模型多个参数不显著，所以对模型参数进行调整.经过多番调整并对模型各个参数进行最小二乘估计和最大似然估计后，疏系数ARIMA（（11，12），1，（1，11））模型各个参数均显著不为零;且残差序列通过白噪声检验，为白噪声序列.所以，确定ARIMA（（11，12），1，（1，11））模型为对广东省肺结核发病例数进行预测是比较理想和合理的最终模型，即

∇12∇xt=εt

εt～NID（0，73.5384）

3 模型拟合及应用

3.1 模型拟合预测效果

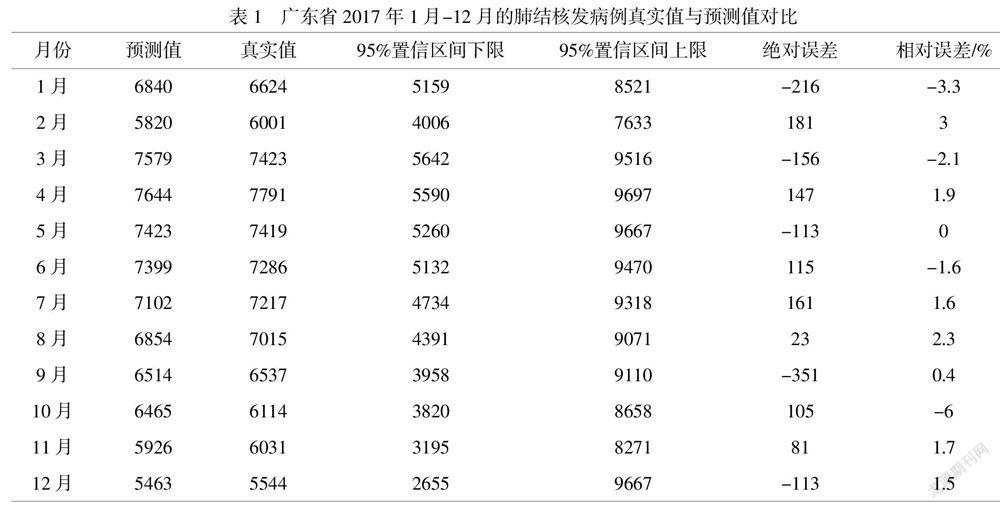
为了检验2节中建立的疏系数ARIMA（（11， 12），1，（1，11））模型的预测效果，将广东省2017年1月—12月的肺结核发病例数进行回代预测.预测结果显示，2017年的3—8月是广东省该年肺结核发病的高发期，4月为最高峰，12月为最低谷，这与实际发病例数和2.1节中得到的序列特征符合.将预测值与真实值作对比，预测值与真实值之间的平均绝对百分比误差（MAPE）为2.12%，在10%的标准以下[4]，且实际发病例数均在预测发病例数的95%置信区间之内，所以可认为该模型属于高精度模型.具体数据请参考表1.

3.2 模型预测应用

使用疏系数ARIMA（（11，12），1，（1，11））模型对广东省2018年1-12月肺结核发病例数进行预测.从预测结果可知，2018年3月-8月依然是广东省肺结核发病高发期，其中最高为4月的7531例，最低为12月的5468例，极值差为2063，较往年相比该年变化幅度不大，总体发病趋势与往年相比无明显变化.2018年各月肺结核发病例数均落在95%的置信区间内，即就预测数据来看，在2018年，广东省并无肺结核病暴发的迹象.

3 讨论

近年来，时间序列的方法与模型越来越多地被应用到传染病的预测中，了解传染病发病趋势和规律、建立良好且敏感的模型拟合并预测，为及时采取有效且迅速措施提供重要理论依据，切实保障人民的身体健康.目前广泛应用到传染病预测的时间序列模型除了ARIMA模型以外，还有混合分解模型、残差自回归模型和GARCH模型等等.如今，ARIMA模型是传染病预测中最常用的模型之一，而疏系数ARIMA模型作为ARIMA模型的推广，使ARIMA模型的定阶与构建更多元化、使用范围更广.预测精度上，疏系数ARIMA模型对残差进行了白噪声检验，当残差通过白噪声检验时，模型已具有较高的精确度[5]-[8].

本研究中主要是采用SAS软件中有关时间序列部分的包，运用最小二乘法和最大似然估计法构建、拟合最佳的模型.经过参数调整后，最终挑选出最优的模型为疏系数ARIMA（（11，12），1，（1，11））模型.在确定模型后，首先使用模型对广东省2017年1月—12月的肺结核发病例数进行预测，将获得预测值与真实值作对比，发现预测值与真实值偏差较小且符合往年发病规律，说明该模型属于高精度模型.然后，再使用疏系数ARIMA（（11，12），1，（1，11））模型预测了广东省2018年1月—12月的肺结核发病例数，根据预测值大致了解2018年廣东省肺结核病的疫情，同时还可以根据当月的真实发病例数是否落入对应的95%预测区间中，初步判断下一个月是否有疫情暴发的可能.因此，可根据本研究中建立的疏系数ARIMA模型，提前预测广东省未来的肺结核月发病例数，提早采取相应的预防控制措施，做好充分准备工作.

参考文献：

〔1〕刘维华，朱建良，郭付爱，等.应用时间序列法建立学校结核病预警模型研究[J].中国学校卫生，2018，39（11）：1682-1685.

〔2〕李晓荣，庞学文，于燕明，等.ARIMA模型在天津市结核并发病预测中的应用[J].实用预防医学，2018，25（12）：1536-1538.

〔3〕王燕.应用时间序列分析[M].北京：中国人民大学出版社，2005.118-121.

〔4〕孙文生，杨汭华.经济预测方法[M].北京：中国农业大学出版社，2005.272-273.

〔5〕刘继恒，白春林，孙要武，等.应用ARIMA模型预测肺结核报告发病例的研究[J].中国热带医学，2014，14（9）：1067-1070.

〔6〕吴祖达.福州市2008-2012年学生肺结核发病特征分析[J].海峡预防医学杂志，2014，20（4）：76-78.

〔7〕孙光，张良，谢金贵，等.ARIMA模型在阜阳市手足口病发病数预测中的应用[J].安徽预防医学杂志，2015，21（4）：231-234.

〔8〕王怡，张震，范俊杰，等.ARIMA模型在传染病预测中的应用[J].中国预防医学杂志，2015，16（6）：424-428.