基于CEEMDAN-PSR-KELM的大坝变形预测

周兰庭　徐长华　袁志美　卢韬

摘要：為提高大坝变形预测精度，针对大坝变形监测序列的非线性、非平稳性等特点，提出一种基于具有自适应噪声的完整集成经验模态分解（ CEEMDAN） -相空间重构（PSR） -核极限学习机（KELM）的大坝变形预测模型。首先利用CEEMDAN算法将大坝变形监测序列分解成为若干不同频率的子序列，然后对各序列进行相空间重构，依据重构的各个子序列分别建立相应的KELM预测模型，最后对各子序列预测结果进行叠加求和得到最终预测结果。通过实例对比分析表明，该模型在大坝变形预测中预测精度较高，对于大坝变形安全监测具有一定的实用价值。

关键词：大坝变形预测;集成经验模态分解;相空间重构：核极限学习机

中图分类号：TV698.1+l

文献标志码：A

doi： 10.3969/j.issn.1000-1379.2019.06.032

大坝系统受到水压、温度、时效以及地质条件等众多复杂因素的影响，变形监测数据往往呈现出强烈的非线性、非平稳性等特征。因此，深入挖掘大坝变形的演变规律，准确预测大坝变形未来的变化趋势，对于评价大坝运行安全状况、保障大坝安全具有重要意义。

目前，针对大坝变形预测的方法主要有统计模型、时间序列分析法、灰色理论、神经网络等[1-2]。然而随着对预测精度要求的不断提高，这些模型与方法在处理大坝非平稳监测数据时往往存在一定的不足，难以充分挖掘大坝变形监测信息内部所蕴含的规律，导致预测精度不够。对此，不少学者尝试将小波分解、EMD、EEMD等非平稳数据分析方法引入大坝变形分析[3-5]，这些方法虽然在一定程度上可以提高预测精度，但在分解过程中也存在一些不足：EMD分解过程中易出现模态混叠现象，对后续预测结果产生较大的影响：EEMD通过添加白噪声来消除模态混叠现象，但由于白噪声分布的随机性以及集成次数的有限性，因此分解后重构信号仍存在一定的噪声残留，影响分解效果，尽管可以通过增加集成次数来降低重构误差，但会显著增加运算量。基于此，本文采用一种具有自适应噪声的完整集成经验模态分解（ CEEMDAN）方法，实现对非平稳时间序列更好的分离，有效改善EMD模态混叠现象，克服EEMD重构误差不为零、分解效率低等问题[6-7]，同时考虑到大坝变形时间序列的混沌特性，采用相空间重构理论对各子序列进行重构处理[8-9]，最后，为进一步提高模型的预测能力，选用拥有更强大的函数逼近能力、处理非线性问题的性能更优的核极限学习机（ KELM）[10—21]来保证模型的预测能力。据此，结合CEEMDAN方法、PSR技术及KELM算法的优势，建立基于CEEMDAN-PSR-KELM的预测模型，将该模型用于某大坝变形预测中，并与单一的KELM模型及EMD-PSR-KELM模型对比，以验证本文模型的有效性。

1 CEEMDAN-PSR-KELM预测模型

1.1 CEEMDAN分解原理

EMD算法是目前常用的非线性、非平稳数据的处理方法，可以将原始信号序列按波动尺度分解为不同频率的IMF分量，实现数据平稳化处理。但EMD分解过程中易出现模态混叠问题，影响数据分解效果。而在此基础上的EEMD算法，通过添加不同的白噪声，进行多次EMD分解后取平均得到最终分解结果，该方法虽可以有效改善EMD分解中的模态混叠问题，但添加的白噪声影响依旧存在，分解后的重构误差难以完全消除，影响数据分解的准确性。CEEMDAN是Colominas在EMD和EEMD基础上，提出的一种具有自适应噪声的完整集成经验模态分解方法。通过在每一次分解过程添加有限次的自适应白噪声，可有效解决EMD分解所产生的模态混叠问题，同时可以克服EEMD分解方法依赖增加集成次数而使重构误差降低的不足，使得在较少的试验次数下，CEEMDAN分解重构误差基本为0，重构信号与原信号几乎完全一致。

1.2 相空间重构理论

相空间重构理论常用于研究混沌时间序列，其基本思想是系统中任一分量的演化都是由与之相互作用的其他分量所决定的，而这些相关分量的信息就隐含在这一分量的发展过程中[9]。因此，可以通过分析某一分量的时间序列，达到重建原非线性动力系统的目的。

1.3 核极限学习机

核极限学习机是在传统极限学习机的基础上，将支持向量机中的核函数引入极限学习机，利用稳定的核映射来替代ELM模型中的随机映射，提升模型的稳定性和泛化能力。由于核函数K（x，y）采用内积的形式，因此在求解模型输出值时只要知道核函数K（x，y）的具体形式即可，而不必知道隐层节点的特征映射函数h（x），也不必设置隐层节点的个数。其算法步骤如下。

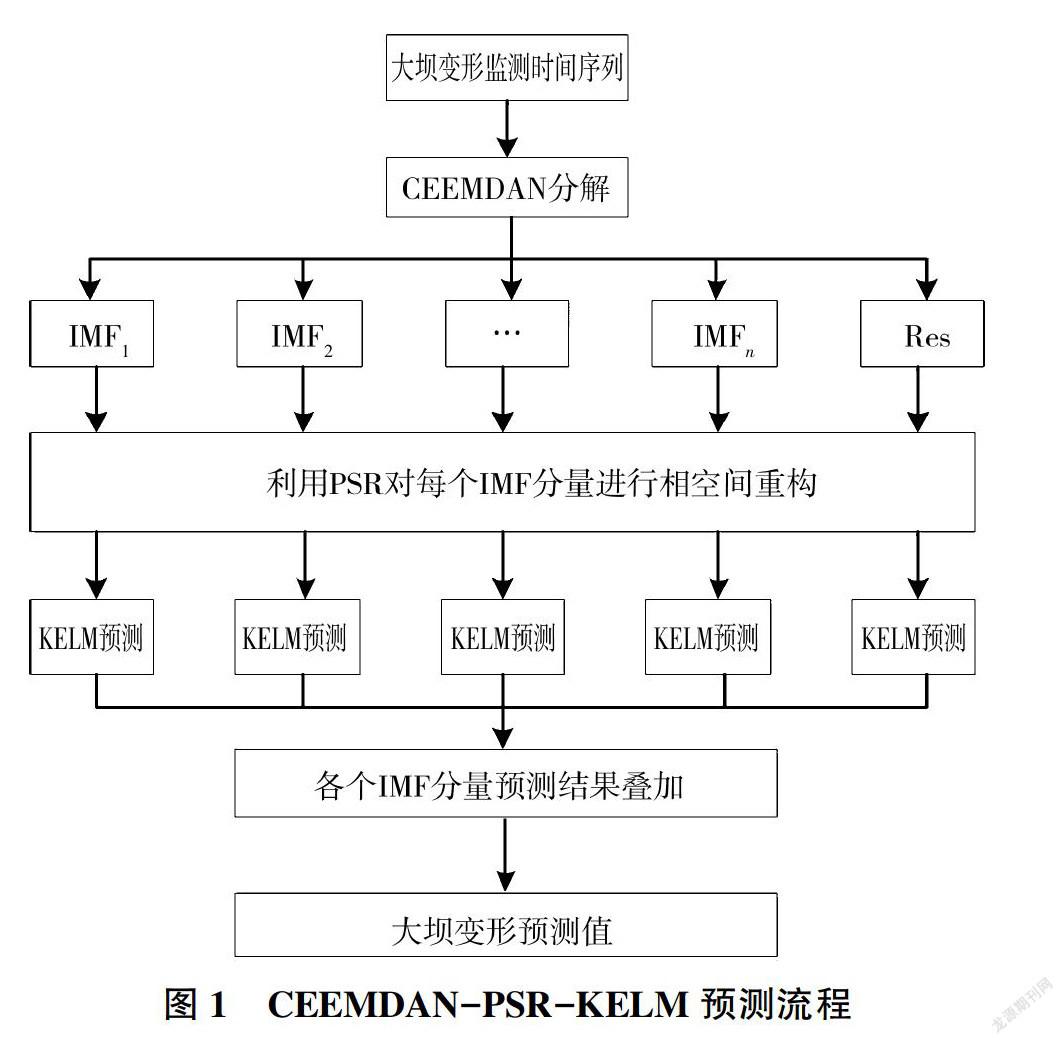
1.4 基于CEEMDAN-PSR-KELM的大坝变形预测方法

基于CEEMDAN-PSR-KELM的大坝变形预测方法建模步骤如下：

（1）采用CEEMDAN算法对大坝变形监测时间序列{x（t）|t=1，2，…，N}进行分解，得到各个IMF分量：

（2）利用PSR技术，对上述各个IMF分量进行相空间重构，确定每个IMF分量的延迟时间τ和嵌入维数m：

（3）针对每个重构的IMF分量，建立相应的KELM预测模型，得到每个IMF分量的预测结果：

（4）将各个IMF分量的预测结果叠加求和，即可得到大坝变形的最终预测结果。

算法流程见图1。

2 算例分析

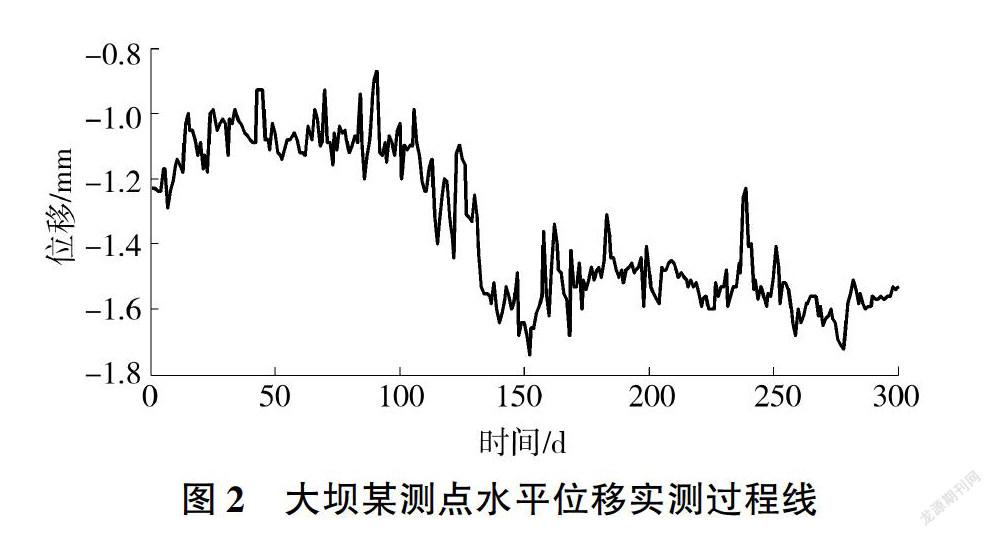
某水库位于福建省金溪干流，库容8.54亿m，正常蓄水位275 m.死水位245 m，拦河大坝为混凝土重力坝，坝顶高程280 m，最大坝高78 m，坝顶全长253m。选取该坝2#坝段某测点垂线监测资料进行分析，取2013年1月1日-2013年10月27日共300组实测数据（见图2）作为样本，其中前250组用于训练拟合、后50组用于模型预测。

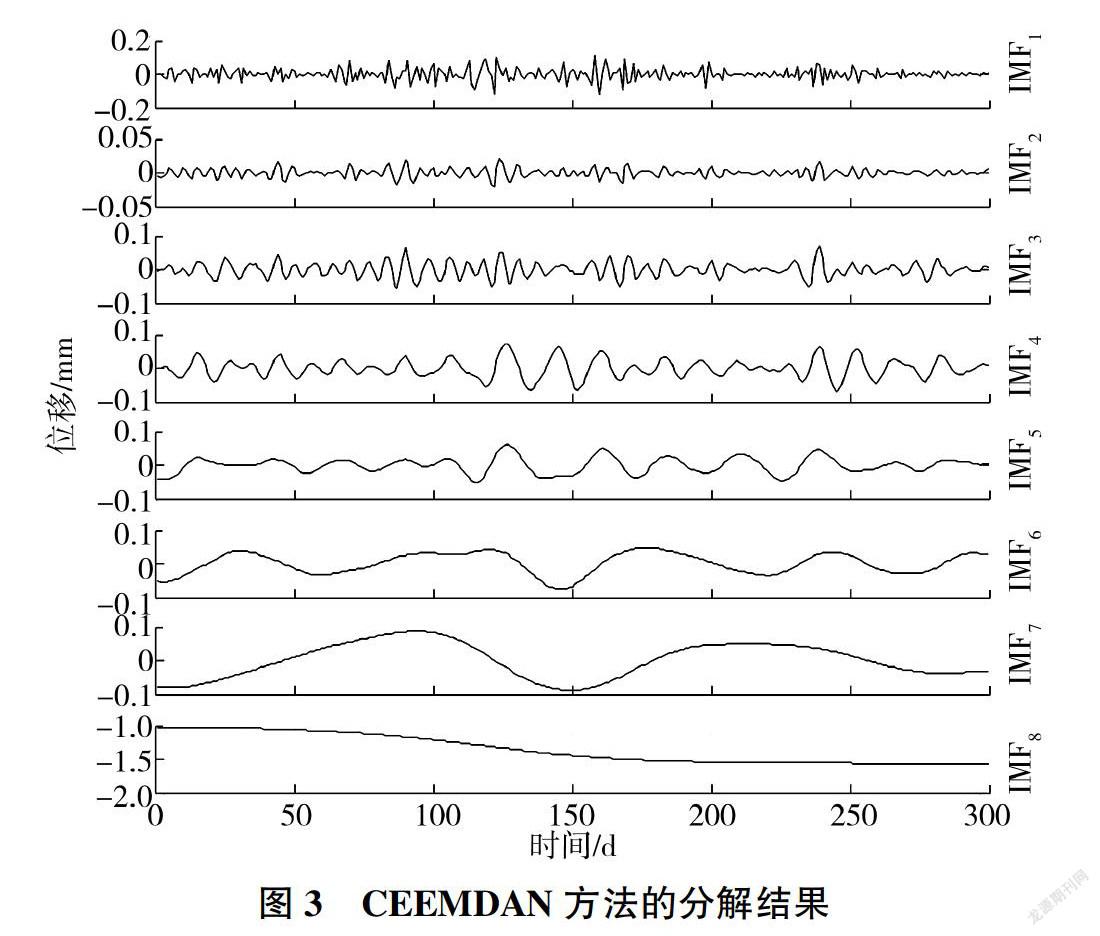
首先采用CEEMDAN算法对大坝实测数据进行分解，得到8个IMF分量，具体分解结果见图3。可以看出，分量IMFl - IMF3波动明显，频率较高，为高频分量;分量IMF4 - IMF6具有一定的周期性波动，主要反映周期项对变形的影响;分量IMF7- IMF8频率较低，为低频分量，主要反映大坝变形随时间的变化。

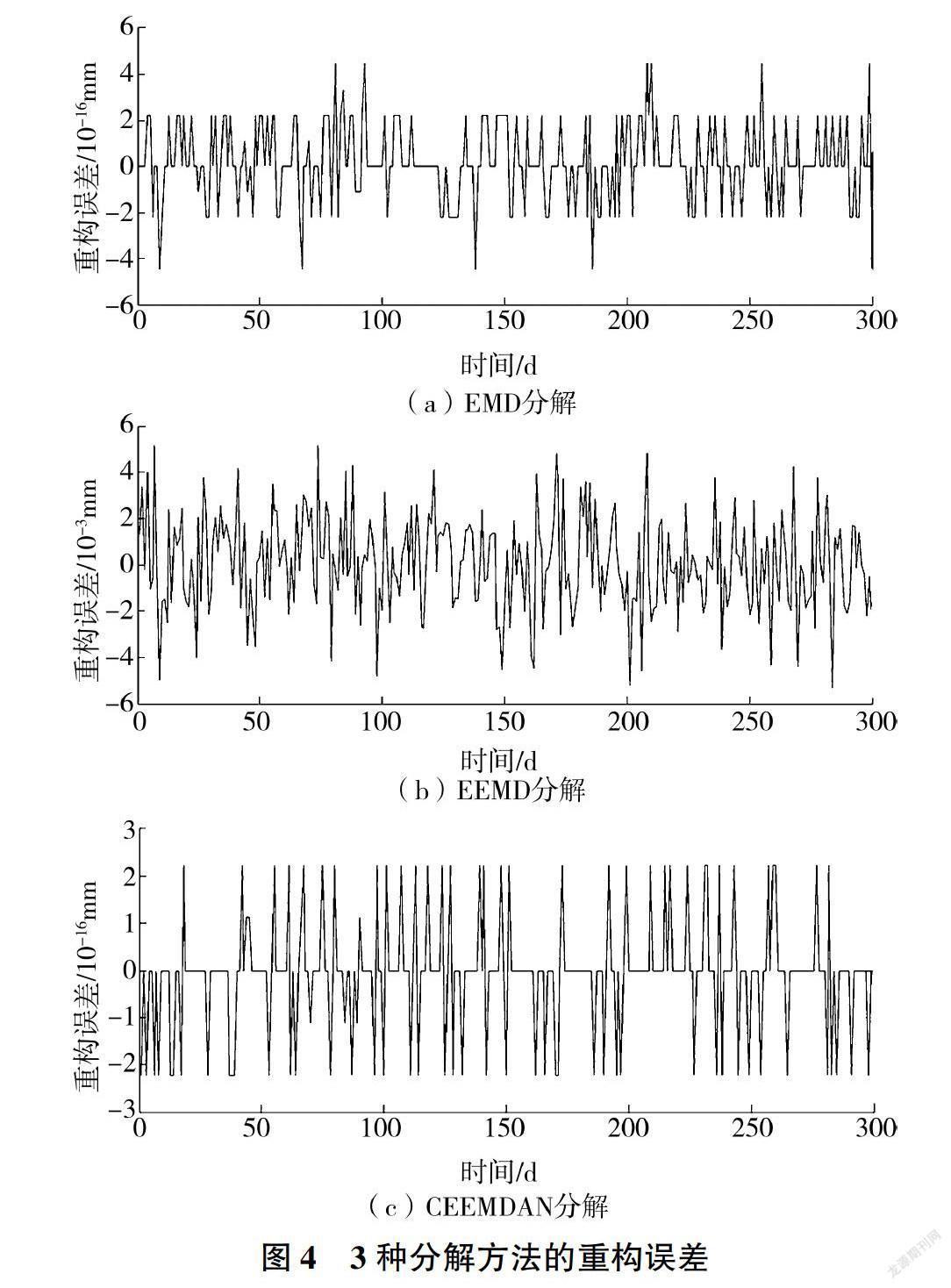
为对比CEEMDAN、EMD、EEMD 3种分解方法的优劣，将大坝原始变形时间序列同时进行EMD、EEMD分解。图4给出了各分解方法的重构误差，可以看出，通过在原始变形时间序列中添加500组白噪声.EEMD分解重构误差较EMD分解明显增大，高出多个数量级，可见EEMD分解后重构信号中依旧含有残余噪声，其重构误差明显受到集成次数的影响：而相较于EEMD分解，序列经过CEEMDAN分解后重构误差显著较低，基本上回到原始EMD分解的量级，说明CEEMDAN算法较EEMD算法精度提升许多，通过白噪声在各个分解阶段的带人抵消，噪声产生的重构误差基本消失，保证了分解的准确性。

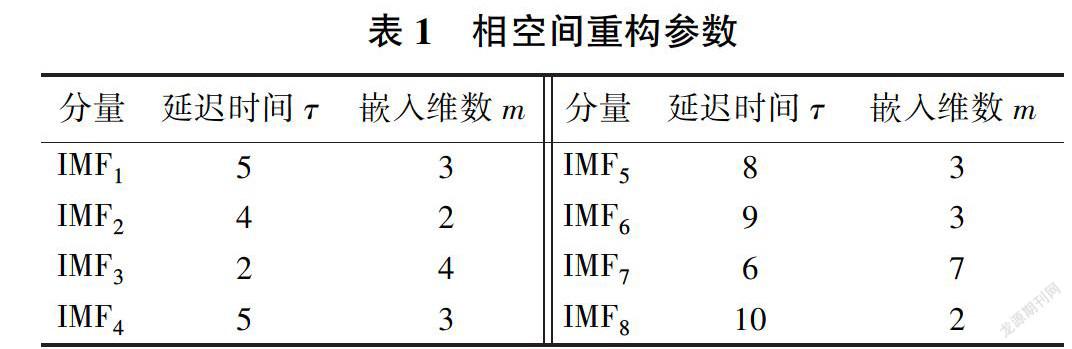
接着，利用PSR理论对分解得到的每个IMF分量进行相空间重构，采用C-C法确定每个分量的延迟时间和嵌入维数，用于确定KELM模型的输入、输出变量。表1给出了各个IMF分量经相空间重构后确定的延迟时间τ和嵌入维数m。

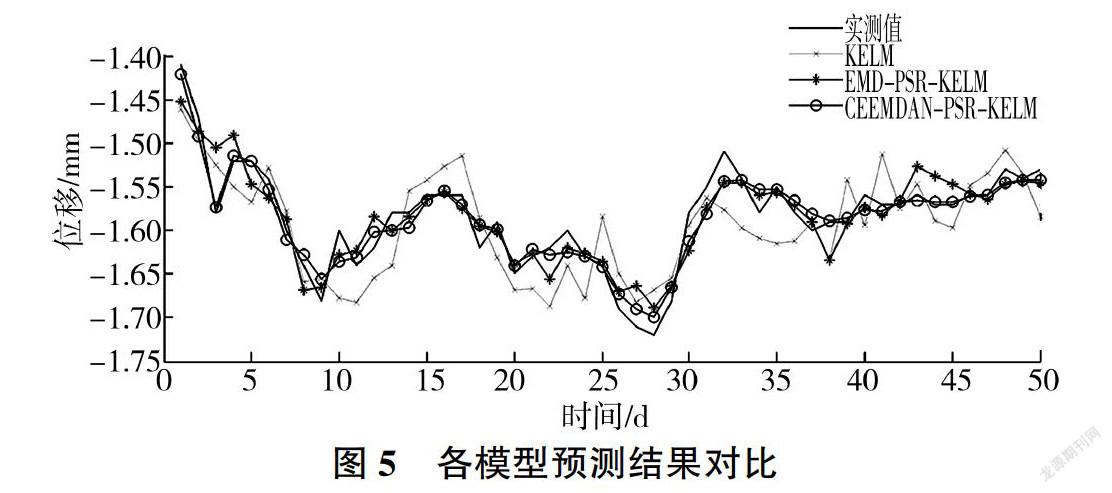
在此基础上，对每个重构的IMF分量分别建立相应的KELM预测模型，以各分量重构后的m维数据作为输入变量，输出变量则为重构后的对应值。其中，核函数选择RBF核函数，惩罚系数C及核参数则采用交叉验证的方式获取，以期获得最优预测结果。最后将每个分量的预测结果进行叠加即可获得最终大坝变形预测值，见图5。

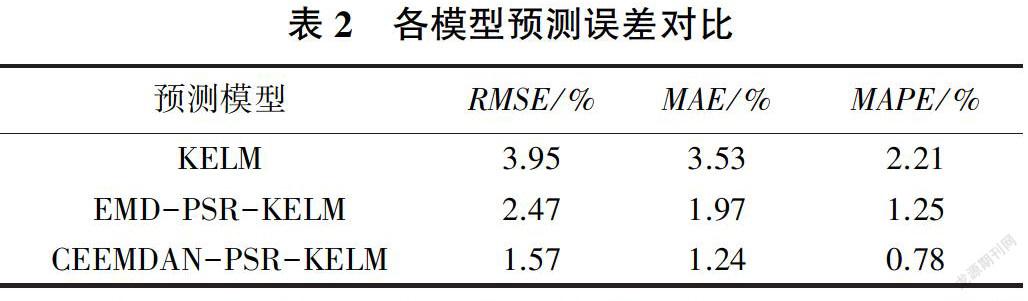
为验证本文模型的有效性与优异性，将其与单一KELM预测模型、EMD -PSR -KELM预测模型进行对比，采用均方根误差（RMSE）、平均绝对误差（MAE）及平均绝对百分比误差（MAPE）3个评价指标来衡量预测精度，见表2。

从图4和表2可以看出，相较于单- KELM预测模型和EMD - PSR - KELM预测模型，本文提出的CEEMDAN-PSR-KELM模型預测值与实际变形监测值非常接近，3个误差性能指标均较小，预测精度明显好于其他两种模型。这说明采用CEEMDAN分解算法和PSR理论能有效挖掘大坝变形非平稳监测数据内部蕴含的规律，提高大坝变形预测精度，在大坝安全监测中具有很高的实用价值。

3 结语

本文结合CEEMDAN技术、PSR理论和KELM模型的优势，提出一种基于CEEMDAN-PSR-KELM的大坝变形预测方法。通过CEEMDAN分解算法将大坝非平稳监测序列分解为若干不同模态分量，并采用相空间重构技术对各个模态分量进行重构，再对重构后的各分量建立KELM预测模型。实例分析表明：基于CEEMDAN-PSR-KELM的大坝变形预测模型能够有效挖掘大坝变形时间序列的变化规律，减小非平稳性对变形预测结果的影响，实现大坝变形的准确预测，在大坝变形监测中具有较强的实用性，为研究大坝变形预测提供了一种新的方法。

参考文献：

[1] 顾冲时，吴中如，大坝与坝基安全监控理论和方法及其应用[M].南京：河海大学出版社，2006：2-7.

[2] 杨杰，吴中如，顾冲时，大坝变形监测的BP网络模型与预报研究[J].西安理工大学学报，2001，17（1）：25-29.

[3]王新洲，范千，许承权，等，基于小波变换和支持向量机的大坝变形预测[J].武汉大学学报（信息科学版），2008，33 （5）：469-471.

[4] 张豪，许四法.基于经验模态分解和遗传支持向量机的多尺度大坝变形预测[J].岩石力学与工程学报，2011，30（增刊2）：3681-3688.

[5]卢献健，晏红波，梁月吉.基于集合经验模态分解和支持向量机的大坝变形预测方法[J].水力发电，2016，42（2）： 38-41.

[6] TORRES M E，COLOMINAS M A， SCHLOrI7HAUER G，et al.A Complete Ensemble Empirical Mode Decompositionwith Adaptive Noise[C ]//IEEE Intemational Conference onAcoustics， Speech and Signal Processing. NJ， USA： IEEE，2011：4144-4147.

[7]贾逸伦，龚庆武，李俊雄，等.基于CEEMDAN与量子粒子支持向量机的电力负荷组合预测[J].电测与仪表，2017，54（1）：16-21.

[8]杨贝贝，基于相空间重构的大坝服役性态小波支持向量机预测模型[J].水利水电技术，2016，47（ 10）：83-87.

[9]胡国杰，魏晓妹，蔡明科，等.混沌一支持向量机模型及其在地下水动态预报中的应用[J].西北农林科技大学学报（自然科学版），2011，39（2）：229-234.

[10]

HUANC G B，ZHOU H， DINC X， et al.Extreme LeamingMachine for Regression and Multiclass Classification[J].IEEE Transactions on Systems Man&Cybemetics Part B，2012，42（2）：513-529。

[11] 刘长良，吴家佳.基于核极端学习机的短期风电功率预测研究[J].热能动力工程，2017，32（1）：95-100.

[12] 郑晓芬，钟旺，李春祥.基于核极限学习机的多变量非平稳脉动风速预测[J].振动与冲击，2017，36（18）：223-230.

【责任编辑马广州】