明流脉动压强特性对自掺气发展影响试验研究

唐毓朔　邓军　卫望汝　龚静

摘要：通过系列模型试验，采用脉动压强仪和针式掺气浓度仪，在不同初始流速与水深条件下详细测量了陡槽自掺气水流沿程各断面掺气浓度与脉动压强，重点分析了脉动压强与掺气浓度分布之间的相关关系，以及断面平均脉动强度对掺气区气泡扩散的影响。试验结果表明：随着明渠水流自掺气沿程不断发展，同一个断面上的脉动压强从断面底部至自由面呈现出先增大后减小的趋势，其中最大值位于断面掺气扩散区：断面平均脉动强度呈现沿程逐渐增大的变化趋势;在不同来流流速、水深及雷诺数条件下，自掺气水流断面平均脉动强度与断面掺气扩散区域之间呈现良好的相关关系。

关键词：明渠;自掺气发展区;掺气浓度;脉动压强

中图分类号：TV135.2

文献标志码：A

doi：10.3969/j.issn.1000- 1379.2019.06.025

随着高坝技术的不断发展，世界各国修建了越来越多的高水头建筑物，泄水建筑物过流流速也在不断增大。当泄水建筑物的水流速度达到一定值时，空气能够通过自由面进入水体，形成掺气水流，也就是水气二相流。掺气后的水气二相流表现为乳白色的水气混合体，其些水力学参数与未掺气的水流有所不同。例如：掺气水流相较于未掺气之前水体膨胀、水深明显增大[1]，水流掺气后对改善水工建筑物空化空蚀有明显作用[2-3]。20世纪以来，许多学者对掺气机理进行了研究。Lane E.W.[4]提出紊流边界层理论，认为当水流紊动边界层发展自由面时，紊流暴露在空气中，水流紊动引起自由面水质点横向脉动流速的动能大于表面张力和重力所做的功时，水质点离开自由面，当水质点重新掉落回水中时，使水流掺气。Hickox P.U.等[5-6]认为紊动与水面相互作用掺气，当水体自由面流速与空气速度不相等时自由面会形成波浪，当自由面水流速度与空气流速的差值大于波浪传播速度时，波浪相对水体有沿水流方向的位移，最终波浪破碎，卷入空气。杨永森等[7-9]对发生掺气的地点、断面掺气浓度以及掺气水深计算方法进行了许多研究，提出了相应的计算公式。吴持恭[1]将掺气区域分成水点跃移区和气泡悬移区两部分计算，得到相应的计算公式，虽然公式简单，与实测资料吻合良好，但有些系数需要进一步研究。卫望汝等[10-12]对掺气发展区流速分布、气泡尺寸分布等进行研究，结果表明，在掺气断面自由面附近气泡直径较大，虽然气泡个数较少，但掺气浓度较高;随着水深的减小，气泡逐渐进入水体内部后，其直径有减小的趋势，虽然气泡个数增多，但掺气浓度较低。

对于明渠自掺气水流，气泡进入水体后，其运动过程、尺寸分布规律及掺气浓度分布规律都可能与水体紊动情况相关，也就与水体的脉动压强及分布规律有关，但到目前为止只知道水流掺气后，水体脉动压强会有所增大，对于具体断面脉动压强的分布规律尚不明确。笔者希望通过对明渠自掺气沿程掺气浓度和脉动压强的测量，得出掺气水流断面压强分布规律，分析其与掺气发展的关系，寻求以紊动强度表征自掺气沿程扩散的规律，以求更加深入、全面地了解明渠自掺气水流发展区的特征。

1 模型试验

1.1 试验装置

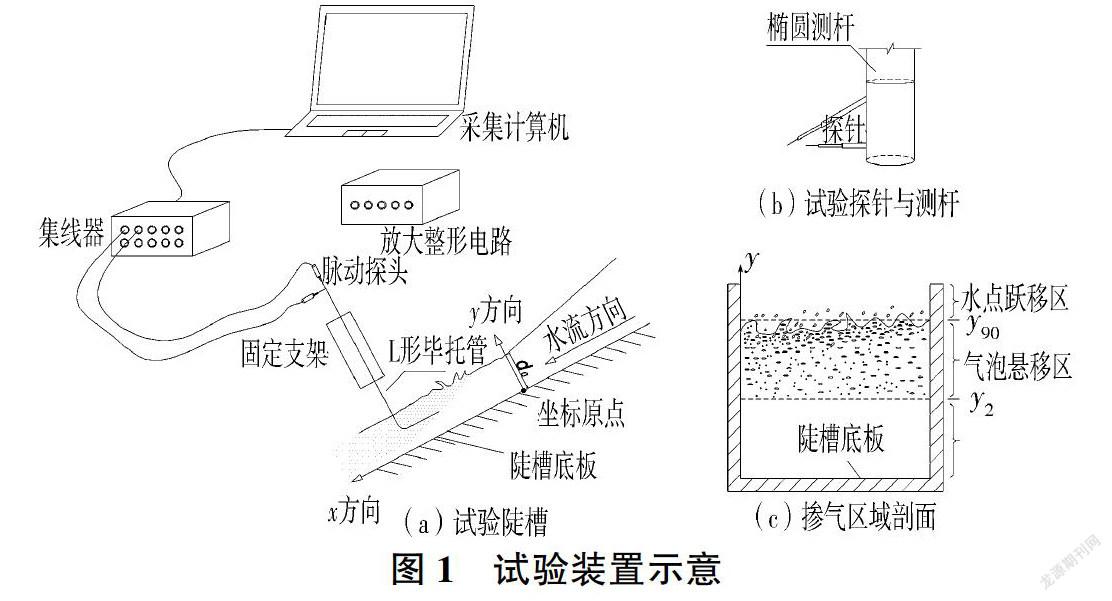
试验装置为四川大学水力学与山区河流开发保护国家重点实验室的大型变坡陡槽系统，该系统由水箱、可调节开度的有压出口段及无压明流段组成，明流段两侧由透明钢化玻璃制成（见图1）。用于试验研究时陡槽坡度为280，长18 m、宽0.3 cm、高0.3 cm，如图l（a）所示。试验中使用CQY-V4.01针式掺气浓度仪对沿程掺气浓度进行测量。根据文献[13 -14]，针式掺气浓度仪对测量模型试验掺气浓度有明显的优势，其主要由感应探针、信号数据收集器和计算机分析系统三部分组成。感应探针的核心是一对铂金丝针型电极，它穿在直径为0.50 mm的不锈钢钢管中，并与信号数据收集器和计算机分析系统相连，最小可检测出直径为0.05 mm的气泡。掺气浓度仪测量原理是：当水和空气通过感应探针时，两者的信号不同，信号经过电脑处理后可记录其变化过程。当探针以频率Fsample（每秒钟采集信号的个数）工作时，设定的测量时间为t，则可以得到txFsample=M个信号，系统自动将这些信号分成水信号和空气信号，并依此计算掺气浓度。感应器采样频率Fsample可以根据针式掺气浓度仪最小气泡感應条件和试验工况流速选取，本次试验研究中，最大流速为7.5 m/s，最小可检测气泡直径为0.05mm，设定采样频率为150 kHz，采样时间设定为Ss。

目前，国内外测量脉动压强普遍采用的是非电量电测法，将非电量转换为电量的传感器有电容式和电阻式两种，电阻式压强传感器因制作简便、工作性能好而被广泛应用于试验研究中15]。本次试验中用于测量脉动压强的是成都泰斯特公司研发的脉动压强测量系统，该系统主要由量程为100 kPa的CY-201型压阻式脉动探头、485-20型数字传感集线器和smartsen-sor4.1计算机分析系统三部分组成。脉动传感器可将压强变化以电流变化的形式展现出来，再经过信号采集器的滤波与放大后，用示波仪进行记录，最终得到脉动压强波形图。

1.2 试验过程

试验时，将脉动探头与6 mm长L形标准毕托管连接，毕托管固定在可上下和左右移动的精密仪器上。为了验证脉动压强测量系统的可靠性，先使用该系统对未掺气清水底流速明渠脉动强度进行测量。为了确定采样时长，在试验前设定采样时长为10、20、60、120s分别测量不同点的脉动数据。结果显示：采样时长为10 s时脉动强度与时长为20、60、120 s时有明显差别，但采样时长为20、60、120 s时脉动强度无明显差别，故本次试验设定采样时长为20 s。

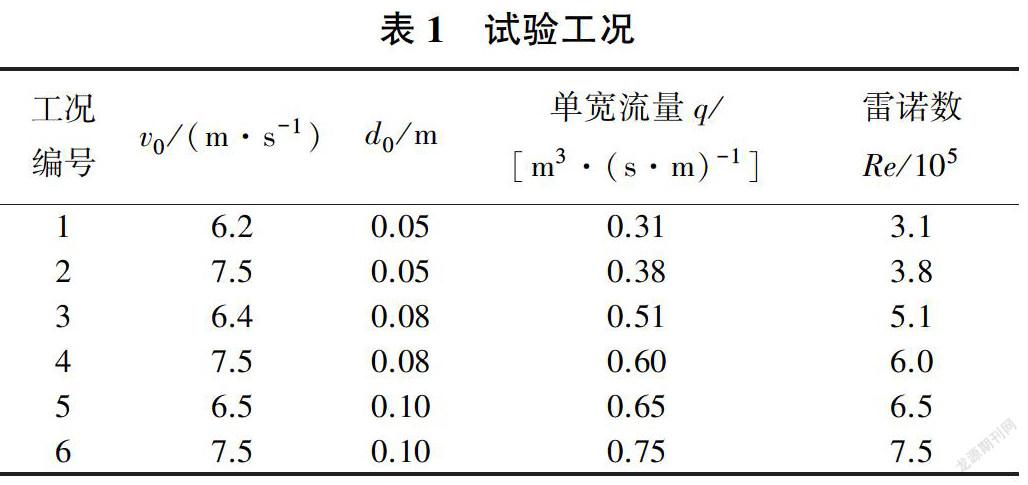
试验分别测量了3种不同开度（ d0=0.05、0.08、0. 10 m）、6种不同水流流量（Q=93、113、154、180、195、225 Us）工况下的数据。为了获得较大出口流速，使水流尽快掺气，所有出流均为有压出流，流速v0范围为6.2 - 7.5 m/s。以出口处为原点，沿水流方向为x方向，水深方向为y方向，测量断面分别距离出口0.3、0.9、2.7、4.2、5.7、7.2、8.7、10.2 m。测量掺气浓度和脉动压强时，各断面最低测点距离陡槽底部距离为3 mm.每两个点之间间隔3 mm.直至测针完全离开水面。测量得到的数据有断面各点掺气浓度、静水压强、动水压强和脉动强度。具体测量工况见表1。

2 结果与讨论

2.1 自掺气水流断面紊动强度与浓度分布规律

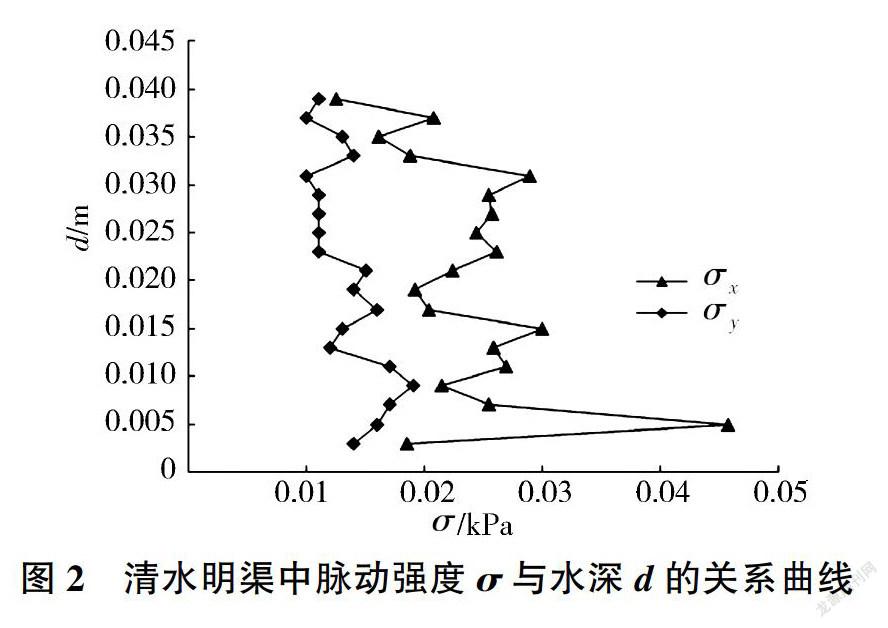
在分析掺气浓度时，定义y2（掺气浓度为2%）对应的水深为掺气的下边界，y2以下区域为清水区，y90（掺气浓度为90%）对应的水深为自由面，y90以上区域为水点跃移区，y2到y90水深区域为气泡悬移区，如图l（c）所示。图2为断面脉动强度与水深的关系，其中σx、σy，分别为x方向和y方向脉动强度。从图2可以看到，脉动强度从渠底至水面呈现先增大后减小的趋势，在靠近渠底附近脉动强度最大，这与参考文献[16]中的脉动压强分布吻合，说明试验设备和测量方法是可靠的。

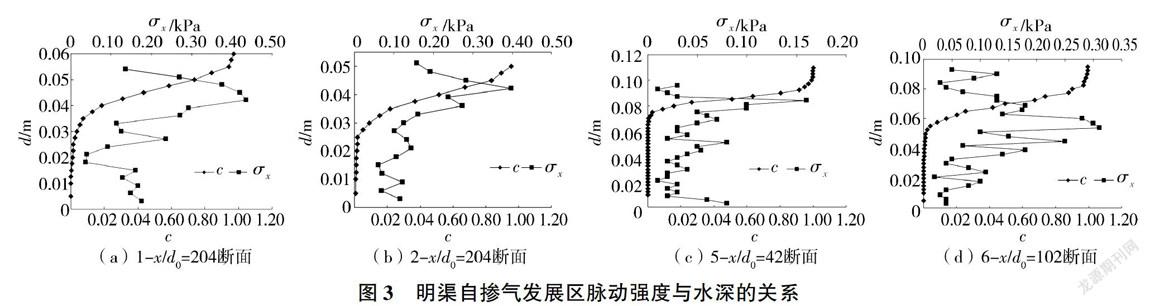
图3为不同工况断面脉动强度与掺气浓度分布图（c为掺气浓度;1-x/d0= 204表示工况1、x/d0= 204断面，其他子图题与此类似）。

在清水区，随着水深的增大，σ在第1个测量点对应的脉动强度值附近震荡，不存在明显的单调性规律。在y2至y90之间的掺气区（气泡悬移区），虽然脉动强度也在不断震荡，但其平均值σm（脉动强度算术平均值）相较于清水区的明显增大。图3（a）中，清水区σm=0.13 kPa，而在气泡悬移区σm=0.24 kPa;图3（b）中，清水区σm=0.10 kPa，气泡悬移区σm=0.21 kPa;图3（c）中，清水区σm=0.04 kPa，气泡悬移区σm=0.06 kPa;图3（d）中，清水区σm=0.09 kPa，气泡悬移区σm= 0.18 kPa。这说明，气泡悬移区的脉动强度明显大于清水区的，掺气区域内水体紊动更加剧烈。由图3可知，不同断面脉动强度均存在一个最大值σmax。图3（a）中，d=0.042 m时o-ax= 0.44 kPa;图3（b）中，d= 0.042 m时o-ax= 0.40 kPa;图3（c）中，d= 0.084 m时σmax=0. 16 kPa;图3（d）中，d= 0.054 m时σmax=0.31 kPa。这说明在掺气断面，虽然脉动强度存在一个最大值，但是这个值所对应的水深不在自由面，也不在渠道底部，而是在水流掺气区内某一水深处。在本次试验范围内，尚不能得出这个脉动强度最大值所对应的具体水深位置，还需要进一步开展试验研究。从不同水流条件、不同断面脉动强度分布规律来看，对于任意一个断面，自掺气水流断面脉动强度整体呈现出先增大、后减小的趋势，并且脉动强度最大值出现在气泡悬移区。在未发生掺气的明渠水流中，虽然脉动强度整体也呈现出先增大、后减小的趋势，但未掺气的明渠水流断面脉动强度最大值在靠近渠底附近，渠底附近脉动强度平均值大于自由面附近的，且自由面脉动强度值最小，这充分体现了掺气水流紊动特性与非掺气水流的显著差异。

分析认为：在未发生掺气的明渠水流中，靠近渠底附近由于水体切应力和水流流速梯度较大，加上渠道底部粗糙度的干扰，涡体往往在渠道底部附近形成，因此在渠底附近脉动强度最大[14]。在掺气水流中，水流流速较大，水体紊动更加剧烈，在渠底附近更容易形成涡体，大量气泡进入水体后，气泡浮力与水体紊动相互作用，相比于非掺气水流，促进了涡体在不同流层之间的紊动交换，气泡个数越多，这种紊动作用的改变越显著。根据对不同掺气水流水气结构的分析研究认为，气泡个数的断面分布峰值位置处于掺气区内部，这也解释了紊动断面分布与掺气浓度断面分布的相关关系。

2.2 自掺气水流沿程断面平均脉动强度与掺气区域变化规律

图4为各工况下断面的平均脉动强度σm、β（β为对掺气上下边界水深进行无量纲化的比值，β= y2/y90，反映了断面掺气区域的大小）随不同断面x/d0变化图，反映了脉动强度与掺气发展的关系。

对比同一工况数据可以发现，随着水流自掺气沿程不断发展，σm不断增大，y2/HO不断减小，说明随着脉动强度不断增大，掺气底缘不断向渠道底部发展，但均未达到渠道底部，说明所有工况测量范围均处在掺气发展区，未达到均匀掺气的状态。

由图4可见，各工况断面平均脉动强度σm沿程不断增大，而卢沿程不断减小。图4（a）中（Re=3.1×10），x/d0=6断面，σm、β分别为0.02 kPa和0.96，发展到x/do= 204断面，σm、β分别为0.19和0.51;图4（f）中（Re= 7.5x105），在x/do=3断面，σm、β分别为0.06 kPa和0.90，发展到x/do= 102断面，σm、β分别为0. 12 kPa和0.65。由于水流紊动和测量误差，因此脉动强度的测量结果有一定的震荡性，但不影响整体规律被揭示。可以看出，不同水流条件下，断面平均脉动强度沿程不断增大，而水深无量纲比值β沿程不断减小。卢沿程不断减小，说明沿程y2与y90的差值增大，气泡悬移区所对应的水深越大，断面掺气区域越大。气泡进入水体后，其运动过程可认为是在紊动作用下的扩散过程[17-18]，由紊動扩散理论可知，气泡在二维垂向上的运动受脉动扩散系数影响，脉动扩散系数越大，进入水体的气泡越容易向水体内部扩散，脉动扩散系数越小，进入水体的气泡越不容易向水体内部发展。一般认为脉动压强是涡体随机掺混、随机运动引起的，脉动强度越大，则涡体随机运动越剧烈，脉动流速也就越大。也就是说，脉动强度越大，则脉动流速越大，同样脉动扩散系数越大，进入水体的气泡越容易向水体内部发展，这也印证了试验结果：随着沿程断面平均脉动强度的不断增大，掺气区域不断扩大，掺气底缘不断向渠底发展。

2.3 自掺气水流紊动强度对掺气区沿程扩散的影响规律

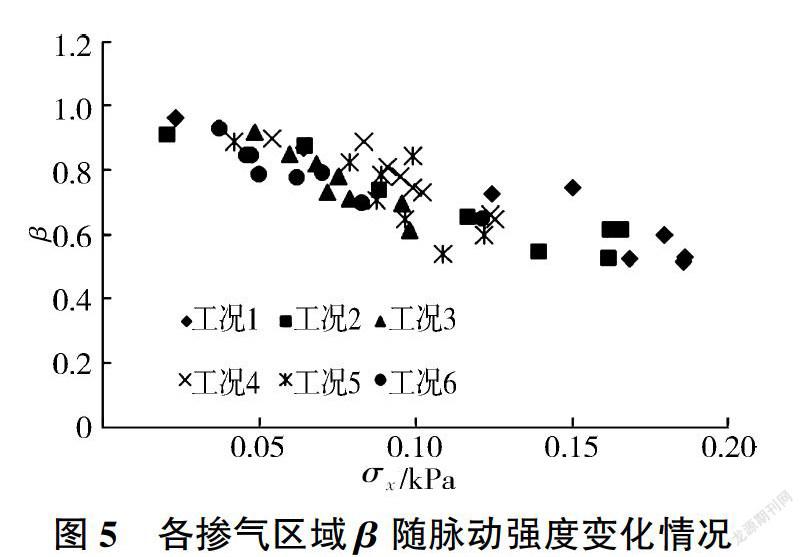
图5为各工况下断面掺气下边界y。与上边界y90的比值β随脉动强度o-的变化图。虽然本试验范围内水流初始雷诺数存在较大差异（工况1中Re=3.1×10，工况6中Re= 7.5x 10），沿程相对发展距离x/do也存在较大差异（工况1从x/d0=6断面发展到x/d0= 204断面，工况6从x/d0=3断面发展到x/d0= 102断面），但从图5看，不同工况下卢与σx存在良好的相关关系。在不同水流条件下，沿程自掺气相对发展距离的差异，导致试验段内自掺气水流断面平均脉动强度存在一定的差异，初始雷诺数较小时，沿程水体脉动变化范围较大，导致下游发展区长度相对更长：初始雷诺数较大时，下游自掺气发展速度更为显著，自掺气水流发展过程中的紊动强度变化范围相对较小。进一步分析，以断面平均脉动强度表征自掺气区域沿程变化可以看出，在自掺气发展区内，相同脉动强度条件下，掺气扩散区域基本一致，二者之间存在良好的相关关系。随着自掺气发展区断面紊动强度的增大，掺气区域不断向水体内部发展，并且不受水流条件差异的影响。比如：工况1中σx由0.04 kPa增大至0.12 kPa时，卢值由0. 92减小至0.73;在工况5中σx值由0. 04kPa增大至0.12 kPa时，卢值由0.93减小至0.65，两者在σx值相近时，β值近乎相等。虽然各工况脉动强度不同，但是随着自掺气区域的不断发展，各工况掺气变化区域基本一致。需要说明的是，本试验采用的是有压出口接明渠的渠道设计型式，由于有压出口断面流速较高，均达到初始断面即发生自掺气所需的水流条件，因此均认为出口位置水流断面为自掺气发生点位置。对于明渠自掺气发展的规律在今后的研究中还需进一步分析验证。

3 结论

针对明渠自掺气水流掺气发展区，通过物理模型试验，测量了沿程各断面脉动压强的强度和掺气浓度，分析了不同断面渠底至自由面x方向脉动压强的变化规律和自掺气沿程发展过程与脉动压强变化的相关关系。结果表明：①在自掺气发展区，同一掺气水流断面x方向脉动强度沿水深方向呈现先增大、后减小的变化规律，掺气区脉动压强大于清水区的，且其峰值位置均出现在断面掺气区内部：②随着自掺气沿程不断发展，自掺气发展区沿程断面平均脉动强度逐渐增大，掺气区域不断扩大，掺气区底缘位置逐渐向渠底发展：③在掺气发展区，掺气水流断面的脉动强度对掺气发展过程有直接影响，不同水流条件下脉动强度与掺气扩散区呈现基本一致的相关关系。

参考文献：

[1] 吴持恭，明渠水气二相流[M].成都：成都科技大学，1989：19-39.

[2] 高月霞，高速水流掺气与通气减蚀的试验研究[D].合肥：合肥工业大学，2005：30-33.

[3] 陈先朴，西汝泽，邵东超，等，掺气减蚀保护作用的新概念[J].水利学报，2003，34（8）：70-74.

[4]

LANE E W. Etrainment of Air in Swiftly Flowing Water[J].Civil Engineering， 1939，9（2）：89-91.

[5] HICKOX P U.Air Entrainment on Spill Faces[J].Civil En-gineering， 1945， 15（ 12）： 562-563.

[6]

VOLKART P.The Mechanism of Air Bubble Entrainment inSelf-Aerated Flow[J].Intemational Joumal of MultiphaseFlow， 1980， 6（5）：411-423.

[7] 楊永森，吴持恭.明渠自掺气水流掺气发展区浓度分布的计算[J].成都科技大学学报，1992（3）：29-34.

[8]杨永森.明渠自掺气水流掺气浓度分布Wood模型的改进研究[J].四川水力发电，1992（2）：45-49.

[9]赵学问，刘善均，董宝顺，明渠自掺气水流发展区掺气浓度分布试验[J].东北水利水电，2007，25（ 12）：35-37.

[10] 卫望汝，邓军，田忠，等，明渠水流自掺气发展区水气结构分析[J].水科学进展，2014，25（5）：704-712.

[11]邓军，许唯临，自掺气水流流速分布[J].水动力学研究与进展，2002.17（3）：369-375.

[12] 卫望汝，明渠水流自掺气发展区掺气特性研究[D].成都：四川大学，2015：52-56，70-90.

[13] 陈先朴，邵东超.掺气水流的气泡尺寸检测[J].水利水电技术，2006，37（ 10）：33-36.

[14]陈先朴.针式掺气流速仪的研制与应用[M].北京：海洋出版社，2000：25-33.

[15]李建中，宁利中.高速水力学[M].西安：西北工业大学出版，1994：67-73.

[16]吴持恭，水力学[M].4版.北京：高等教育出版社，2008：133-142.

[17] HUBERT C，GONZALEZ C A.Physical Modelling and ScaleEffects of Air-Water Flows on Stepped Spillways[J].浙江大学学报A（应用物理及工程版）（英文版），2005（3）： 36-43.

[18] 周云，光滑矩形槽中横向紊动扩散系数的研究[J].甘肃科学学报，1995（2）：8-12.