基于蚁群算法的层状结构介电特性反演方法

丁鑫　郭乙霏　万宏远　刘小梅　张小旺

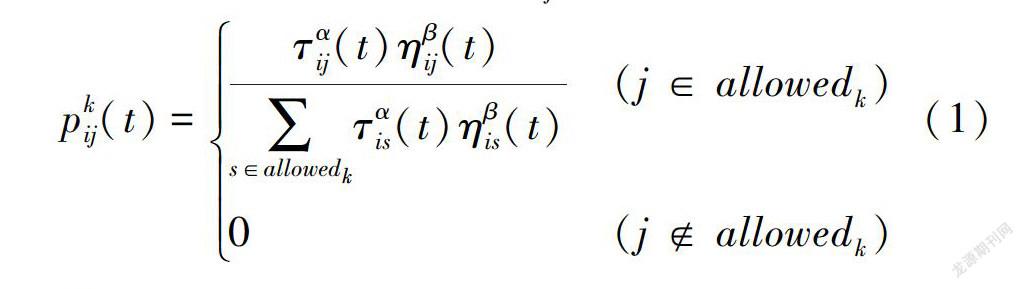
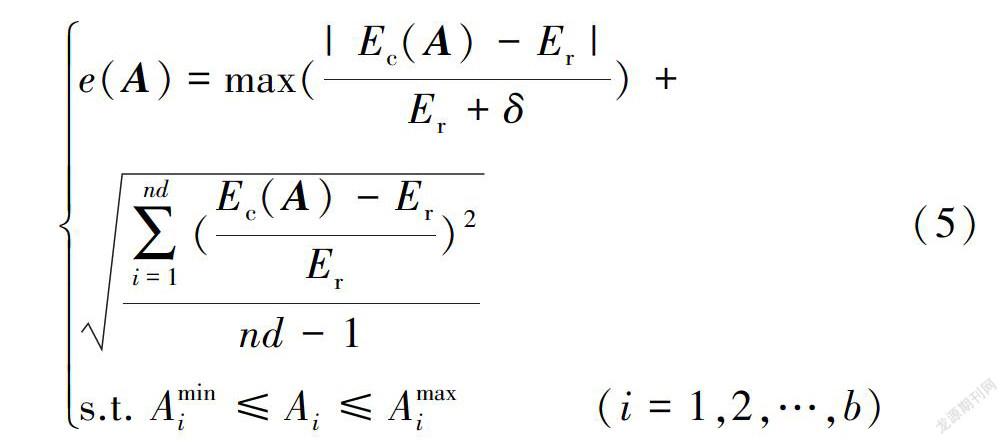
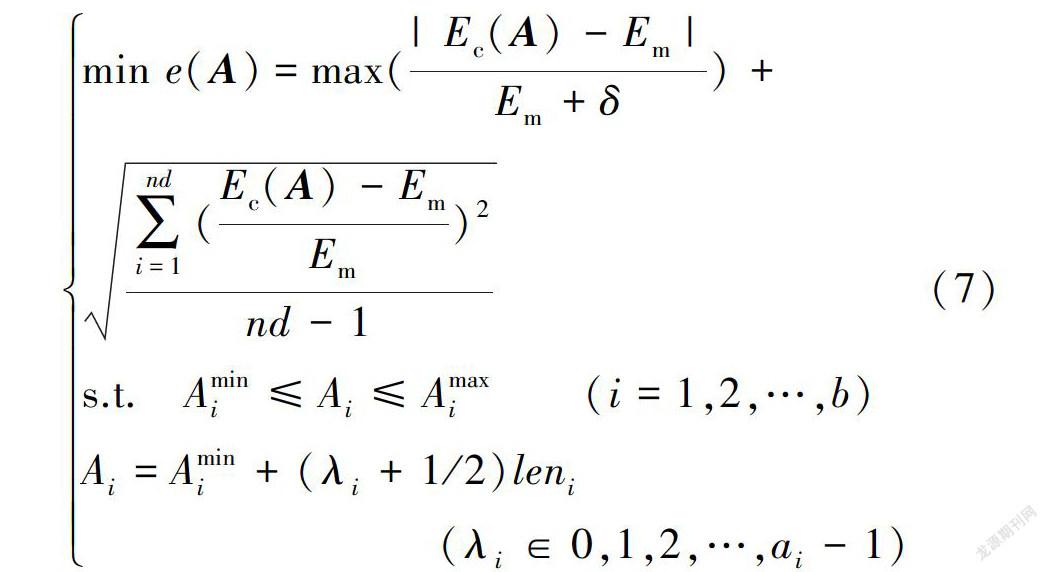
摘要：探地雷达凭借其高效、连续、无破损等优点，已广泛应用于水利、道路、市政等工程质量评估与隐患探测中。通过对探地雷达回波信号进行反演分析，可以得到结构内部情况。本文基于一种适用于连续优化问题的改进蚁群算法，建立了道路、堤坝、隧道等层状结构体系介电特性反演算法，实现了结构层介电参数和厚度的智能优化识别。理论模型验算结果表明，该方法可准确收敛至理论值，误差满足要求。利用该方法分析实际路面雷达回波信号，反算路面结构层厚度，并与钻芯取样结果进行对比，结果显示，反算结果误差在4%以内。

关键词：层状结构：介电特性;蚁群算法;反演分析;结构层厚度

中图分类号：TP301.6

文献标志码：A

doi：10. 3969/j .issn. 1000- 1379.2019.06.024

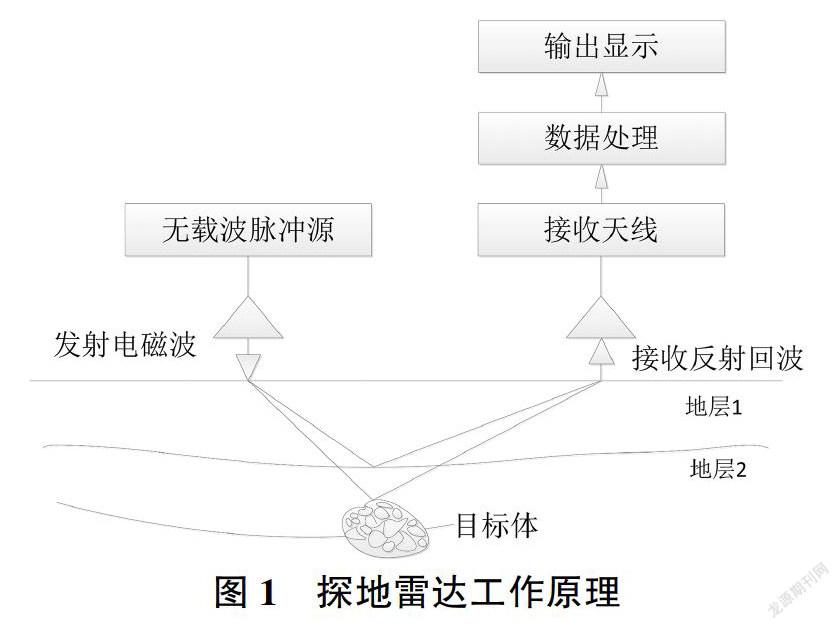
探地雷达（ GPR）作为一种高效、连续、无破损的地球物理探测手段，已经在水利、交通、市政等工程的质量评估与隐患检测中广泛应用。其检测原理如图1所示：由地面发射天线向地下发射高频电磁波，电磁波在地下层状结构传播过程中，遇到目标体或结构层分界等材料特性发生改变的界面后，将会产生折射、反射、绕射现象，反射波回到地面后被接收天线接收，通过对探地雷达反射信号进行分析，可解译出目标深度、介质结构及性质等信息。

探地雷达反演算法目前主要包括传统经典反演算法和现代智能反演算法两类。传统经典算法主要包括单纯形法、最速下降法、牛顿法等，这类算法收敛速度快，但存在稳定性较差、反演结果受参数初值选取的影响等问题[1]。近年来模拟退火算法、遗传算法、神经网络算法、粒子群算法、蚁群算法等现代智能反演算法逐渐被应用到工程结构反分析领域。其中，蟻群算法凭借其适应范围广、全局寻优能力强、适宜并行运算、易于与其他优化算法结合等优点，已经被应用于路面结构层模量反演[2]、交通流量分析[3]等领域。

蚁群算法是意大利学者Dorigo根据对蚂蚁觅食行为的研究，提出的一种群体智能优化方法[4]。蚂蚁在自然界寻觅食物过程中，当遇到含有多条未知路径的路口时，会在其所选择通过的路径上留下一些信息素，后面的蚂蚁如果再来到这个路口时，选择有信息素路径的概率较大，这样就能形成一个正反馈，最优路径上积累的信息素越来越多，其他路径上的信息素则越来越少，最终整个蚁群都能寻找到巢穴与食物源间的最短路径。

本文基于一种改进的蚁群算法对探地雷达回波信号进行反演分析。首先通过一个理论模型验证算法的反算精度，然后应用该算法分析实测高速公路探地雷达回波信号，并将反算结果与钻芯取样结果进行对比，验证算法对实际工程的适用性。

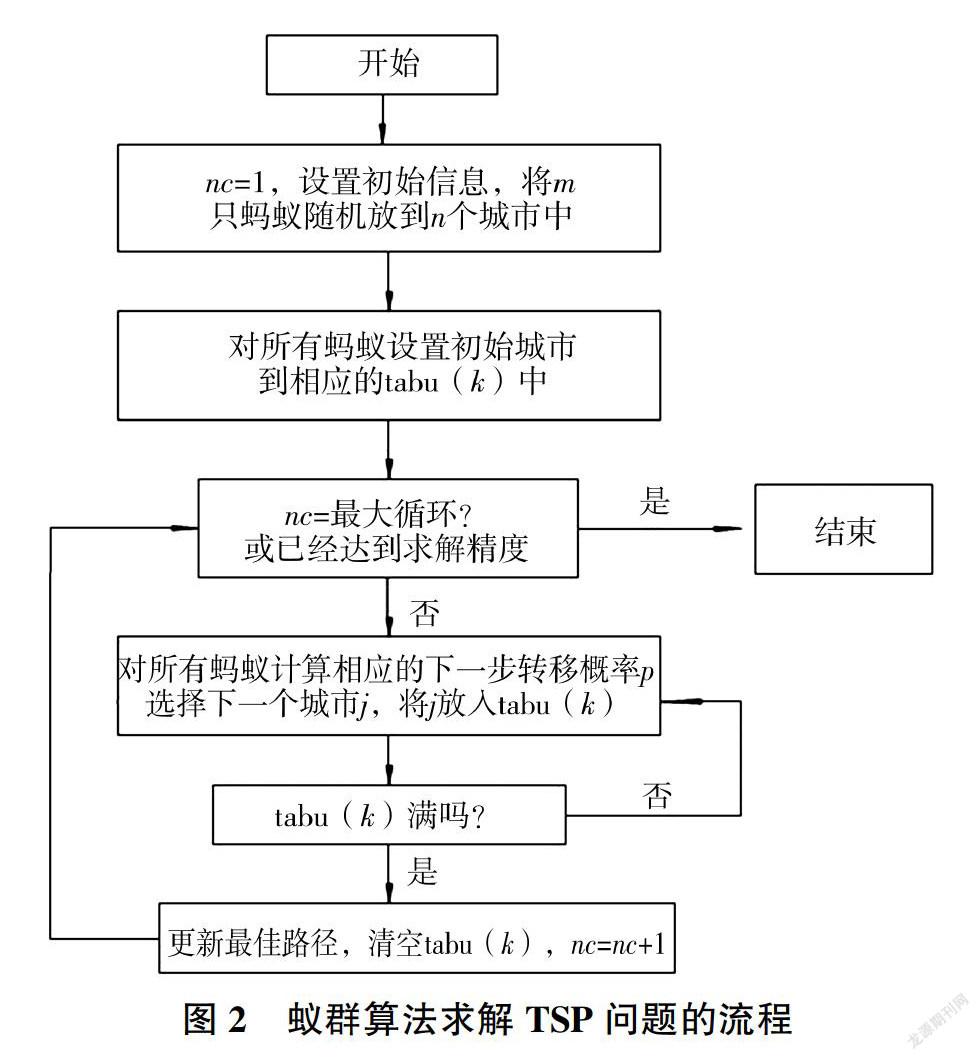
1 蚁群算法基本原理

2 基于改进蚁群算法的层状结构介电特性反演

层状结构介电特性蚁群反演优化算法，即根据GPR实测回波信号，基于蚁群优化算法，寻找一组使模拟信号误差最小的结构层介电参数。

由于反演过程是通过拟合探地雷达反射波波形实现的，因此目标函数确定为雷达实测反射信号与模拟反射信号关键控制点处（波峰、波谷等）幅值的均方误差与最大相对误差之和，即：

3 算例分析

3.1 算例一

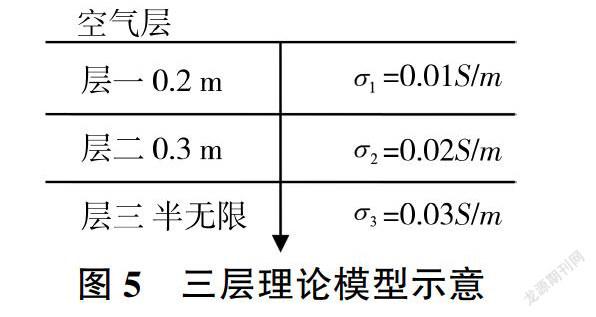
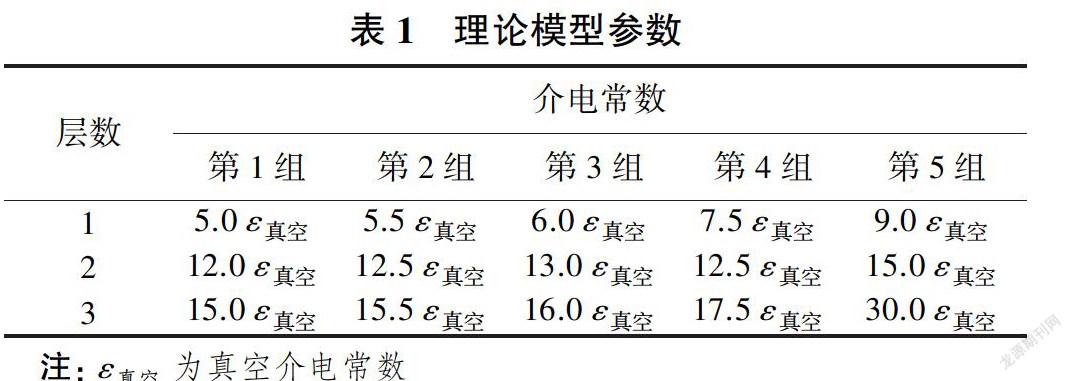
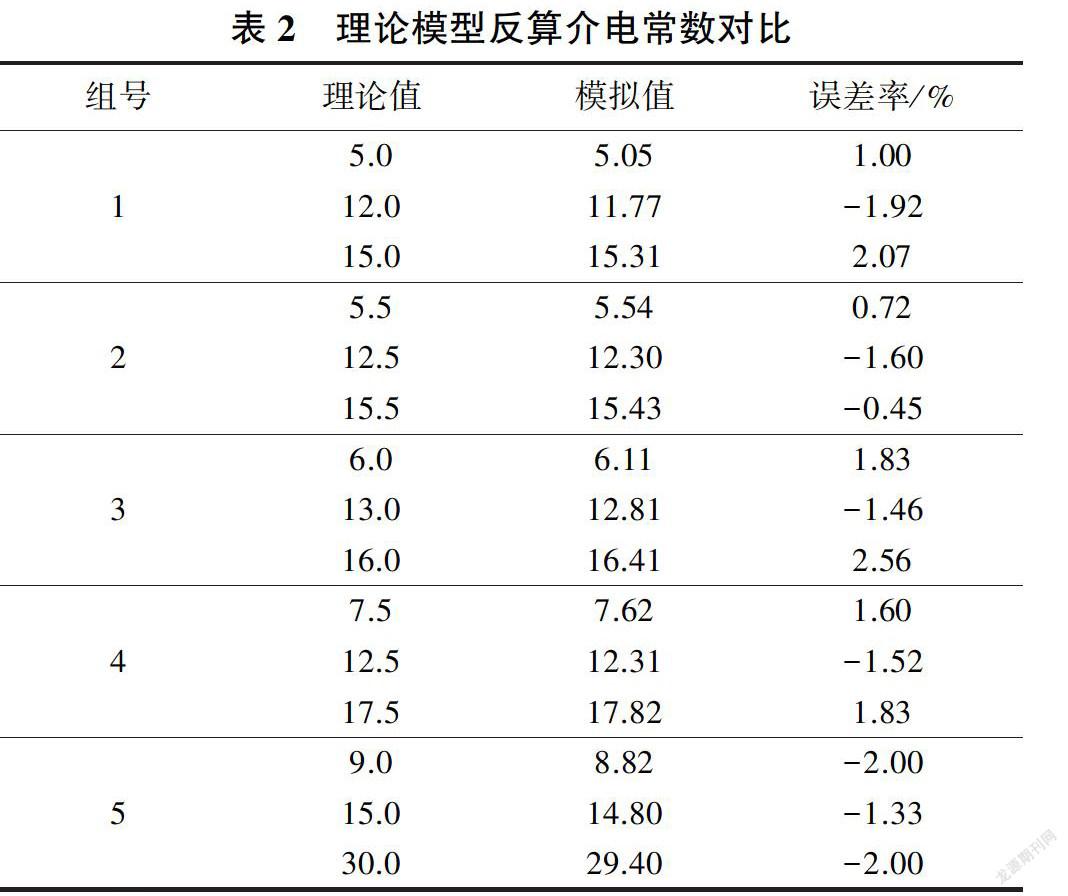
利用图5所示3层结构理论模型验证蚁群算法反算层状结构介电参数的精度，层状结构上部为空气，电导率为0。利用表1给出的5组数据，基于时域有限差分方法可以计算得到5条反射波形。3层理论模型的层厚和电导率选取如图5所示，以这5道波形为拟合目标，分别采用蚁群算法进行反演分析，反演结果见表2。

由表2可知，改进的蚁群算法能够较好地收敛到真实值，介电常数的反算误差率在3%以内。

3.2 算例二

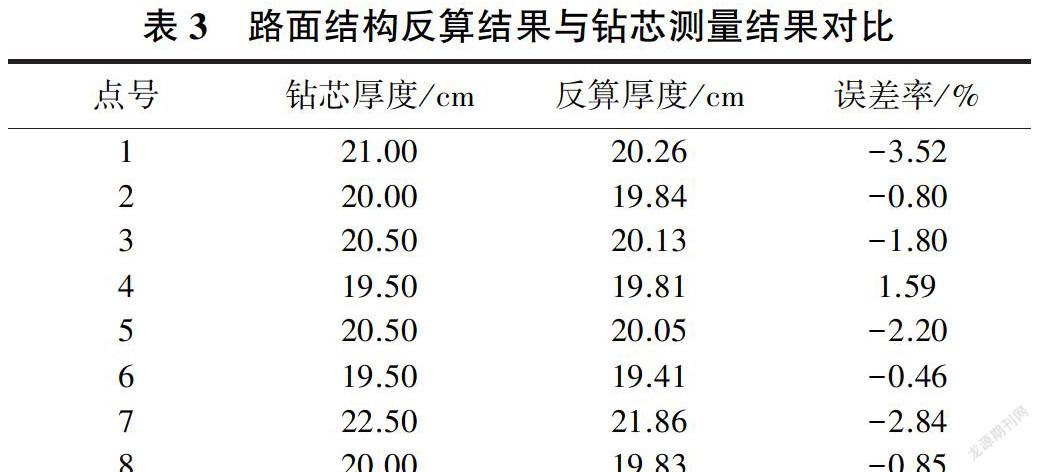
某高速公路设计为四层，面层为20 cm沥青混凝土，基层为20 cm水泥稳定碎石，底基层为35 cm石灰土，下部是半无限土基，测试雷达为Rodar V型路面雷达。表3对比了测试点的取样厚度与算法厚度相对误差率。

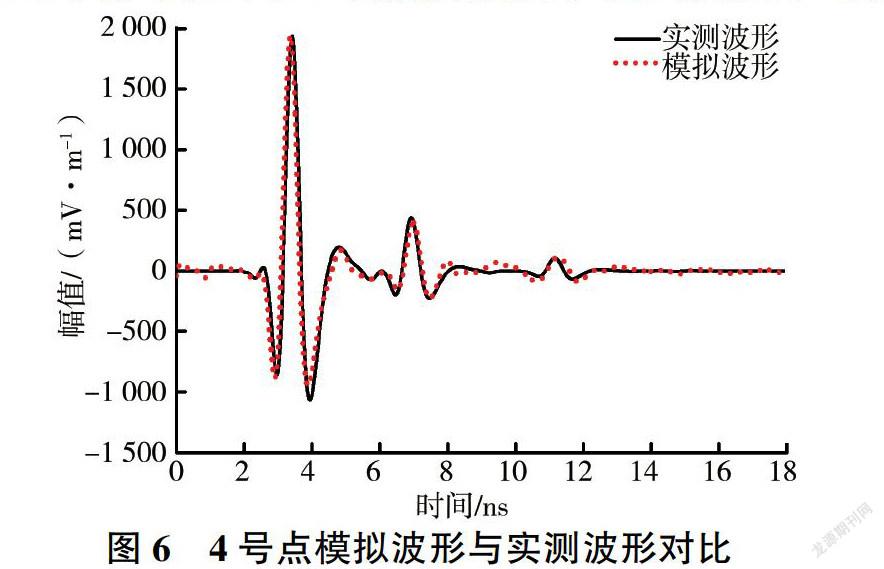
由表3可知，反算结果和钻芯结果误差率均控制在4%以内。图6为4号点模拟波形和实测波形对比。

4 结语

基于改进的蚁群算法建立层状结构介电特性反演方法，通过理论模型反演介电参数。为了验证此算法的精度，选取8个取芯点实测雷达波形，采用本文算法对路面厚度进行反演分析，通过对比钻芯与蚁群算法反演计算结果可知，精度基本满足要求。

参考文献：

[1] 方宏远.基于辛算法的层状结构探地雷达检测正反演研究[D].大连：大连理工大学，2012：10-14.

[2] 王复明，刘小梅，蔡迎春.蚁群算法在路面模量反演中的研究与应用[J].路基工程，2009（4）：74-75.

[3] 常玉林，汪小淳，张鹏.改进蚁群算法在交通分配模型中的应用[J].郑州大学学报（工学版），2017，38（2）：41-45.

[4]DORICO M.Optimization， Leaming and Natural Algorithms[D]. Milan： Politecnico di Milano， 1992： 30-62.

[5] LIN S，KERMCHAN B W. An Effective Heuristic Algorithmfor the TSP[J].Operations Research，1973， 21（2）：498-516.

[6] 田明俊，智能反演算法及其应用研究[D].大连：大连理工大学，2005：23-42.

【责任编辑张帅】.