物质点法在椭圆骨料混凝土损伤模拟中的应用

邹家强 张巍 刘爱华

摘要：为研究混凝土結构的宏观力学响应及损伤行为，应用物质点法这一新型数值方法对椭圆骨料混凝土进行数值模拟研究。基于蒙特卡罗模拟方法，考虑混凝土的细观结构，提出了一种构建随机椭圆骨料混凝土细观几何模型的方法。在该几何模型的基础上，进一步提出一种快速建立混凝土细观物质点模型的方法。分别以弹塑性损伤本构模型和弹性本构模型模拟砂浆和骨料的力学行为，采用开发的物质点法程序对混凝土数值模型进行了单轴拉伸及单轴压缩数值试验。结果表明，物质点法模拟所得的结果与设计规范及有限元结果相近。可见，物质点法为混凝土结构损伤行为的数值模拟提供了一条可行的途径。

关 键 词：混凝土; 损伤行为; 物质点法; 蒙特卡罗模拟方法; 椭圆骨料

混凝土的多尺度实验与数值模拟已成为研究者们更准确了解混凝土材料与结构的力学响应及其内部损伤行为的重要手段[1]。一般而言，在细观尺度下，混凝土被认为是由骨料及砂浆两者组成。而在大多数混凝土结构中，粗骨料的体积占比高达40%～50% [2-3]，因此骨料的级配及分布对混凝土的宏观力学响应有着显著而直接的影响。为了开展骨料级配及分布对混凝土的力学行为的研究，研究者们通常采用物理试验和数值试验两种主要手段。由于混凝土试块的制备及后期养护需要消耗大量的人力、物力及时间，导致研究效率的降低，因此，数值试验在研究混凝土结构问题上得到越来越多学者们的重视。

目前混凝土细观数值模拟采用的数值方法主要为有限元法[4-8]。和传统有限元法相比，物质点法（MPM）作为一种新型无网格数值方法，采用质点来离散材料区域，因而可以方便地利用混凝土细观数字图像的像素点信息进行建模，同时可以在数值计算时避免传统有限元法在大变形情况下的网格畸变[9]。然而，目前物质点法的应用领域主要集中在爆炸、冲击、流固耦合、滑坡等极端变形问题上[10-13]，在混凝土结构内部损伤演化问题上的应用研究仍相对缺乏。

为此，本文首先提出一种快速建立随机椭圆骨料混凝土结构物质点模型的方法。随后结合特定的弹塑性损伤本构模型，编制相应的物质点法程序，从细观角度模拟其结构的损伤演化，进而探讨物质点法在该问题上的适用性，以期能为混凝土结构损伤行为的数值模拟提供一种新的数值方法。

1 物质点法基本理论

物质点法采用拉格朗日质点离散材料区域，并用欧拉背景网格计算空间导数和求解动量方程。由于兼具拉格朗日算法和欧拉算法的优势，物质点法较好地避免了网格畸变和对流项处理。基于求解控制方程的方法，物质点方法也被细分为显示或隐式物质点法。本次研究采用的是显式物质点法，其基本理论及控制方程表述如下。

在计算过程中，物质点法是利用中心差分法对背景网格结点的运动方程进行求解，得到当前时间步的每个背景网格节点的位移增量，再通过求解建立在网格节点上的有限元插值形函数 NI（xi） 映射得到每个物质点的位移增量及其他物理量。由于物质点法在求解动量方程时，采用更新拉格朗日格式，每个时间步内，物质点是与背景网格固定一起运动的。在上一时间步结束后，抛弃变形后的计算网格，但在下一时间步，仍使用初始时刻的物质点网格（即欧拉网格）作为运动方程的集成，单个时间步的运动如图1所示。由于形函数插值初始时刻的欧拉网格布置方便，集成简单，由此，即可快速实现物质点与背景网格节点之间信息的映射。

由于结合了欧拉算法与拉格朗日算法的优势，一方面，物质点法在每一时间步开始，利用欧拉网格集成动量方程，可有效避免网格畸变问题;另一方面，在每一计算步中，它采用更新拉格朗日形式，如此又可避免因对流项造成数值耗散而导致计算效率降低的问题。综上所述，物质点法是一种采用物质点离散、每个时间步都重置计算网格的数值算法，被认为是一种特殊的有限元法。

2 数值计算模型

由上述基本理论可知，物质点法的背景计算网格和质点网格两者既是相互独立，又是相互统一的，结合运用马怀发等学者提出的随机椭圆骨料模型[3-4]，几何框架下的混凝土计算模型通过物质点法便能快速高效地生成。在生成的随机椭圆骨料模型基础上，通过将不同的信息分别映射到质点网格中，即可生成分别带有砂浆、骨料信息的物质点，随后将两种物质点拼接，即可生成相应的计算模型，其生成步骤见图2。

以建立随机椭圆骨料占比为45%的50×50大小的混凝土结构模型为例，从开始到完成建模平均耗时为10 min，而在相同条件下，有限元法的建模时间平均耗时在30 min左右[5]。

从图2可直观看出，物质点法是基于像素进行计算模型构建的方法。由于大多数几何图形通常是以数字图像进行处理，如电脑断层扫描，或细观甚至微观下的混凝土观测图像等，在这样的情况下，物质点法就比有限元法可以更快速直接对这些图像进行数值空间离散化，即把每一个图片中的像素点转换成带有特定信息的物质点。近几年来， CT技术已逐渐开发应用于探测混凝土内部的裂缝发展[14-15]，由于其图片也是像素显示方式，因此也能够与物质点法建立一定的匹配关系[16]。反之，物质点法也可根据既定图像构建与之对应的数值模型，随后通过计算也可进行分析对比。

3 本构模型

4 模拟分析及讨论

4.1 建模与结果分析

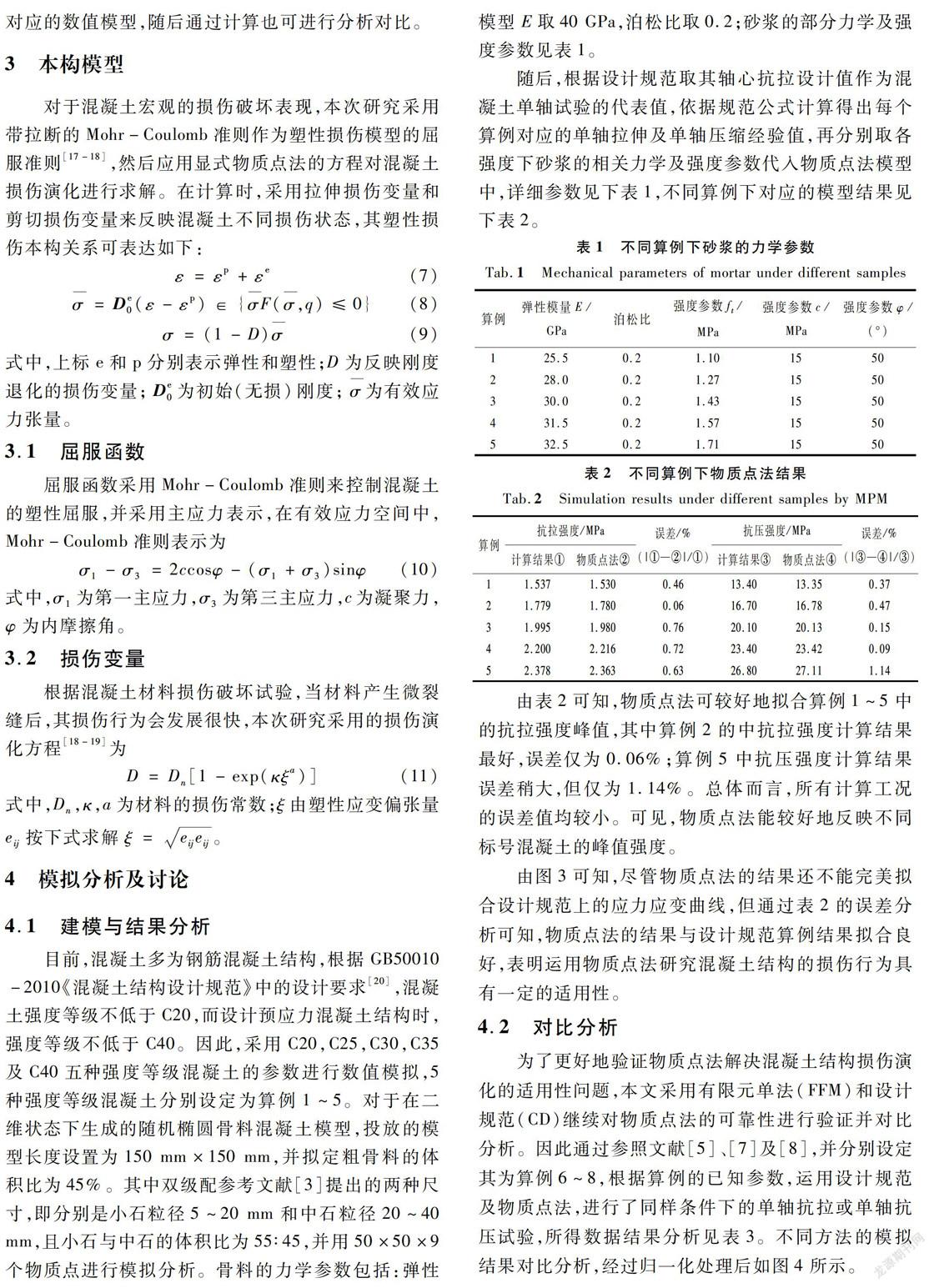
目前，混凝土多为钢筋混凝土结构，根据GB50010-2010《混凝土结构设计规范》中的设计要求[20]，混凝土强度等级不低于C20，而设计预应力混凝土结构时，强度等级不低于C40。因此，采用C20，C25，C30，C35及C40五种强度等级混凝土的参数进行数值模拟，5种强度等级混凝土分别设定为算例1～5。对于在二维状态下生成的随机椭圆骨料混凝土模型，投放的模型长度设置为150 mm×150 mm，并拟定粗骨料的体积比为45%。其中双级配参考文献[3]提出的两种尺寸，即分别是小石粒径5～20 mm和中石粒径20～40 mm，且小石与中石的体积比为55∶45，并用50×50×9个物质点进行模拟分析。骨料的力学参数包括：弹性模型E取40 GPa，泊松比取0.2;砂浆的部分力学及强度参数见表1。

随后，根据设计规范取其轴心抗拉设计值作为混凝土单轴试验的代表值，依据规范公式计算得出每个算例对应的单轴拉伸及单轴压缩经验值，再分别取各强度下砂浆的相关力学及强度参数代入物质点法模型中，详细参数见下表1，不同算例下对应的模型结果见下表2。

由表2可知，物质点法可较好地拟合算例1～5中的抗拉强度峰值，其中算例2的中抗拉强度计算结果最好，误差仅为0.06%;算例5中抗压强度计算结果误差稍大，但仅为1.14%。总体而言，所有计算工况的误差值均较小。可见，物质点法能较好地反映不同标号混凝土的峰值强度。

由图3可知，尽管物质点法的结果还不能完美拟合设计规范上的应力应变曲线，但通过表2的误差分析可知，物质点法的结果与设计规范算例结果拟合良好，表明运用物质点法研究混凝土结构的损伤行为具有一定的适用性。

4.2 对比分析

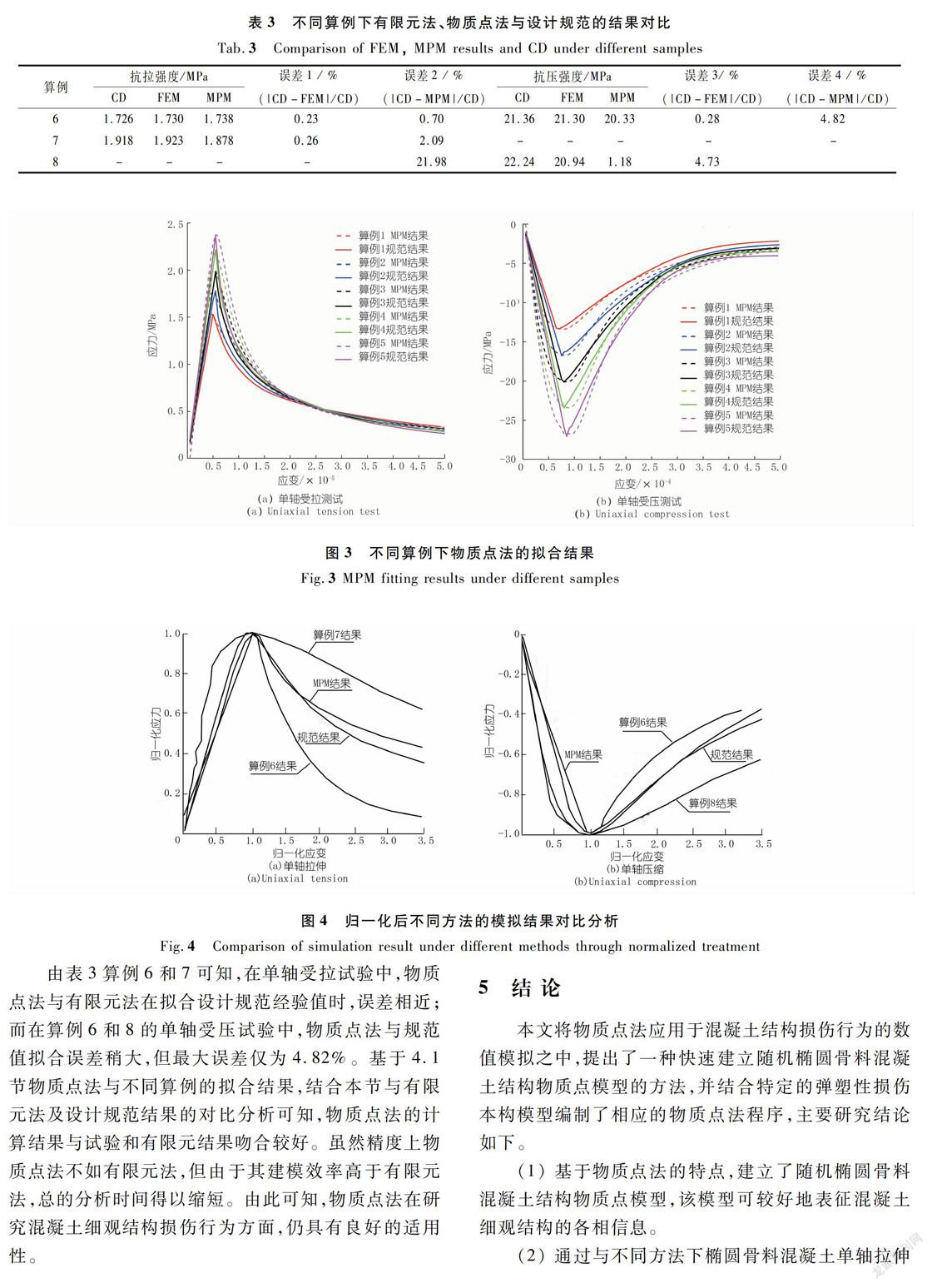
为了更好地验证物质点法解决混凝土结构损伤演化的适用性问题，本文采用有限元单法（FFM）和设计规范（CD）继续对物质点法的可靠性进行验证并对比分析。因此通过参照文献[5]、[7]及[8]，并分别设定其为算例6～8，根据算例的已知参数，运用设计规范及物质点法，进行了同样条件下的单轴抗拉或单轴抗压试验，所得数据结果分析见表3。不同方法的模拟结果对比分析，经过归一化处理后如图4所示。

由表3算例6和7可知，在单轴受拉试验中，物质点法与有限元法在拟合设计规范经验值时，误差相近;而在算例6和8的单轴受压试验中，物质点法与规范值拟合误差稍大，但最大误差仅为4.82%。基于4.1节物质点法与不同算例的拟合结果，结合本节与有限元法及设计规范结果的对比分析可知，物质点法的计算结果与试验和有限元结果吻合较好。虽然精度上物质点法不如有限元法，但由于其建模效率高于有限元法，总的分析时间得以缩短。由此可知，物质点法在研究混凝土细观结构损伤行为方面，仍具有良好的适用性。

5 结 论

本文将物质点法应用于混凝土结构损伤行为的数值模拟之中，提出了一种快速建立随机椭圆骨料混凝土结构物质点模型的方法，并结合特定的弹塑性损伤本构模型編制了相应的物质点法程序，主要研究结论如下。

（1） 基于物质点法的特点，建立了随机椭圆骨料混凝土结构物质点模型，该模型可较好地表征混凝土细观结构的各相信息。

（2） 通过与不同方法下椭圆骨料混凝土单轴拉伸及压缩试验结果的对比分析，验证了编写的物质点法计算程序的准确性，表明物质点法能有效模拟混凝土结构的力学响应及损伤演化，具有良好的适用性和应用前景。

参考文献：

[1] Wang X F，Yang Z J，Yates J R.Monte Carlo simulations of mesoscale fracture modelling of concrete with random aggregates and pores[J].Construction and Building Materials，2015，75：35-45.

[2] Wang Z M，Kwan A K H，ChanH H C.Mesoscopic study of concrete I：Generation of random aggregate structure and finite element mesh[J].Computers and Structures，1999，70（5）：533-544.

[3] Ma H F，Xu W X，Li Y C.Random aggregate model for mesoscopic structures and mechanical analysis of fully-graded concrete[J].Computers and Structures，2016，177：103-113.

[4] 杨华，李宗利，惠弘毅.基于随机骨料模型的混凝土弹性模量预测研究[J].长江科学院院报，2016，33（2）：100-105.

[5] Xu Y，Chen S H.A method for modeling the damage behavior of concrete with a three-phase mesostructure[J].Construction and Building Materials，2016，102：26-38.

[6] Omidi O，Lotfi V.Finite Element Analysis of Concrete Structures Using Plastic-Damage Model in 3-D Implementation[J]. International Journal of Civil Engineering，2010，8（3）：187-203.

[7] 许叶帅.考虑骨料形状的混凝土细观模型研究[D].南京：东南大学，2017.

[8] 周尚志.混凝土动静力破坏过程的数值模拟及细观力学分析[D].西安：西安理工大学，2007.

[9] Nguyen V P.Material point method basics and applications[D].Wales：Cardiff University，2014.

[10] 吴金国，林庆华，弯港，等.基于物质点法的轨道炮刨削机理三维数值研究[J].爆炸与冲击，2017，37（2）：307-314.

[11] 张雄，刘岩，张帆，等.极端变形问题的物质点法研究进展[J].计算力学学报，2017，34（1）：1-16.

[12] 王斌，冯夏庭，潘鹏志，等.物质点法在边坡稳定性评价中的应用研究[J].岩石力学与工程学报，2017，36（9）：2416-2155.

[13] 张巍，史卜涛，施斌，等.土质滑坡运动全过程物质点法模拟及其应用[J].工程地质学报，2017，26（3）：815-823.

[14] Ren W Y，Yang Z J，Rajneesh S，et al.Two-dimensional X-ray CT image based meso-scale fracture modelling of concrete[J].Engineering Fracture Mechanics，2015，133：24-39.

[15] Henry M，Darma I S，Sugiyama T.Analysis of the effect of heating and recuring on the microstructure of high-strength concrete using X-ray CT[J].Construction and Building Materials，2014，67：37-46.

[16] Homel M A，Herbold E B.Field-gradient partitioning for fracture and frictional contact in the material point method[J].International Journal for Numerical Methods in Engineering，2017，109（7）：1013-1044.

[17] 常曉林，马刚，刘杏红.基于复合屈服准则的混凝土塑性损伤模型[J].四川大学学报（工程科学版），2011，43（1）： 1-7.

[18] 张巍，肖明，范国邦.大型地下洞室群围岩应力-损伤-渗流耦合分析[J].岩土力学，2008，29（7）：1813-1818.

[19] Franttziskonis G， Desai C S. Constitutive model with strain softening[J].International Journal of Solids Structures，1987，23（6）：733-750.

[20] 混土结构设计规范：GB50010-2010 [S].北京：中国建筑工业出版社，2011.

（编辑：郑 毅）