大学数学与专业课的相关性分析

李静 万波

摘要：通过对学生成绩的统计分析和相关性检验可以看出，大学数学成绩的好坏对专业课的影响是明显的，具备较丰富的数学知识和较好的数学素养是专业学习和可持续发展的重要途径.因此，在教学上应把握人才培养目标，从教育的高度认识大学数学教学，有效整合教学内容，践行大学基础数学教学为专业服务的理念.

关键词：大学数学;专业课;多元线性回归;相关性分析;可持续发展

中图分类号：O13;G64  文献标识码：A  文章编号：1673-260X（2019）08-0005-03

1 引言

大学数学课程是高校大学生极其重要的公共基础课，不仅为学生专业课的学习奠定坚实的数学知识基础，而且对于培育学生严谨的思维能力，务实严谨的科学态度都具有重要意义，对大学生可持续发展能力的培养有着其他学科无法比拟的重要作用.那么大学基础数学学习的好坏，对其后续专业课程的学习有多大程度的影响？大学数学课程与专业课之间有着怎样的关系呢？

本文拟从大学数学教学改革为切入点，在江汉大学文理学院新生财管专业组织实验班，本着同学们志愿报名原则，在实验班增加基础数学（包括高等数学，概率论与数理统计，线性代数）课时，优化教学内容，改革教学方法，两年后抽取16级财管实验班和16级财管普通班的成绩，在对两个班大学数学成绩和专业课成绩的统计分析基础上，也对大学数学基础课与专业课的相关性进行了研究和分析.

2 描述性统计分析

针对成绩的基本描述，我们选取了最小值（Min），最大值（Max），中位数（Median），均值（Mean），标准差（Sd）这五个基础统计量，其中最小最大值以及标准差可以让我们大致了解数据的波动范围和波动程度，而均值和中位数则分别从数值上的平均和顺序上的中间两个角度来描述数据的中间水平.

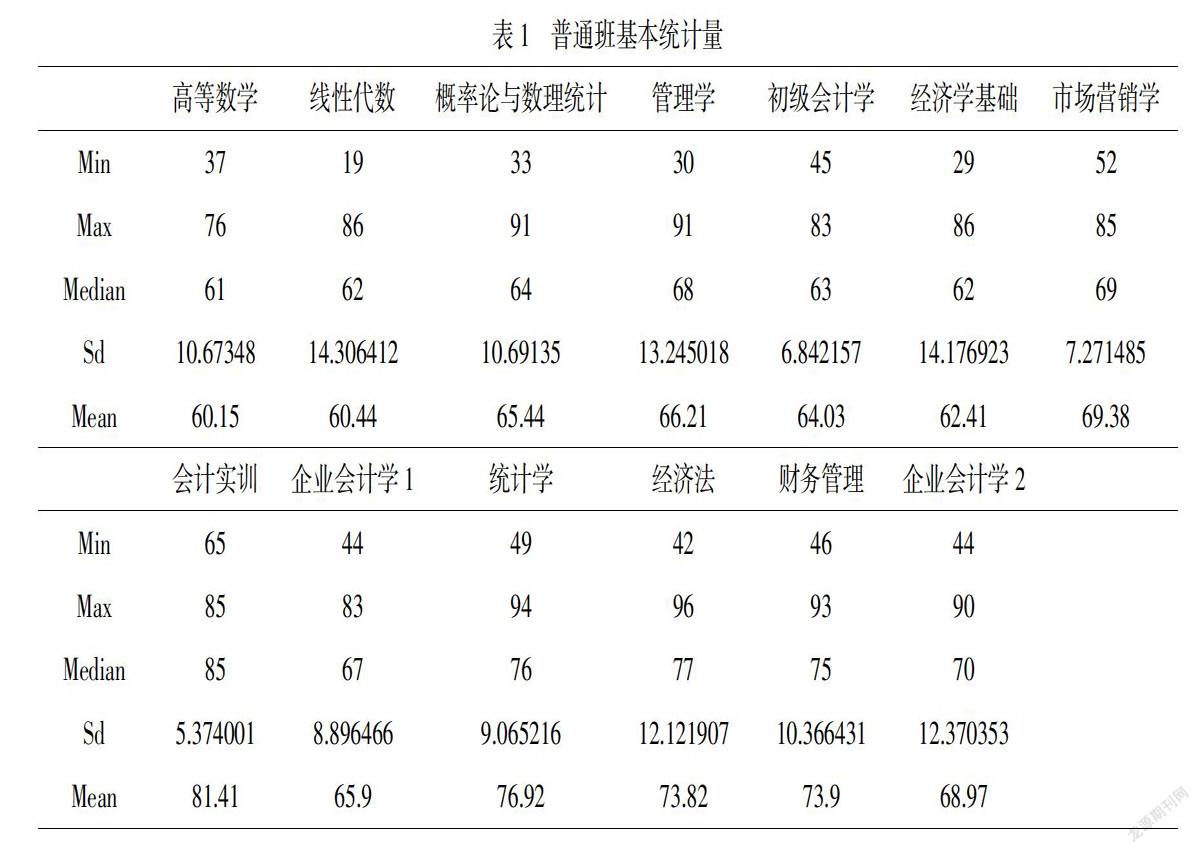
根据表1，从均值和中位数来看，二者相差不大，说明整个班的课程中成绩基本集中在中间水平，极端成绩很少.而所有课程的平均分均在60分及格线以上，整体成绩良好.但数学类课程的中间水平在60左右，而核心类课程的中间水平要相对高一些，大部分处于60～80，说明数学能力相对薄弱;从最小最大值和标准差来看，数学类课程的最低分最高分都相对较低，也能在一定程度上说明其数学能力相比其他课程明显弱势.课程的标准差都集中在10左右，除了会计模拟实训这门课，标准差最小，说明在这门课上学生成绩差异最小;线性代数、管理学和经济学基础的标准差较大，表明学生之间的差距较大，成绩分布更加宽泛.

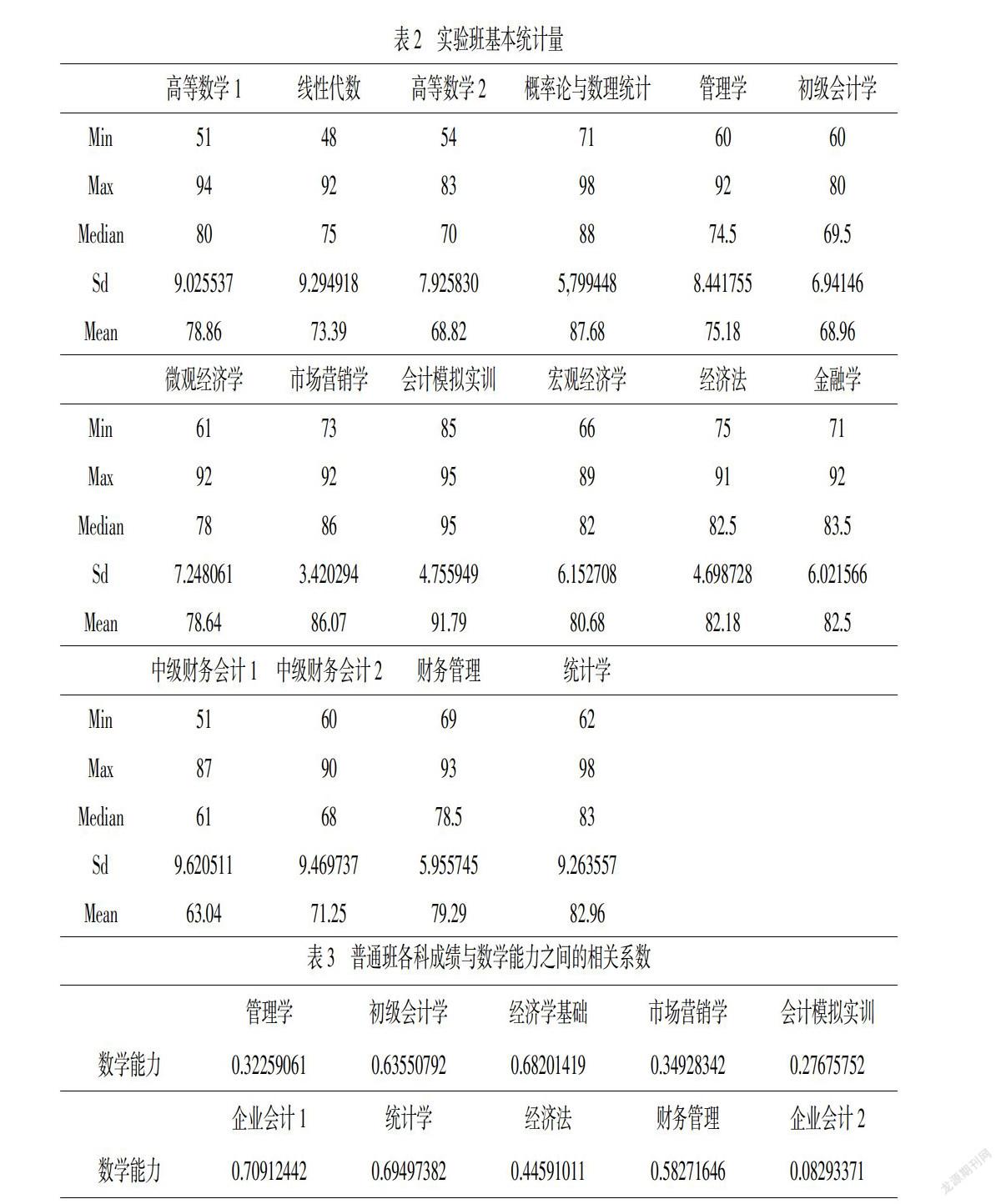
针对实验班的16门课程进行描述性统计，根据表2，从均值和中位数来看，二者差距也很小，所以极端成绩很少.所有课程的平均分均在60分及格线以上，14门课程平均分在70以上，7门课程平均分在80分以上，整体成绩相比普通班更为优秀.尤其实验数学类课程的中间水平大致在70～80，明显成绩方面更加优异，虽然数学类课程更多，但数据表现依然稳定，说明总体来看数学能力要远优于普通班;从最小最大值和标准差来看，对比普通班，实验班成绩分布更窄，最低分最高分相对较大，各门课程的标准差均小于10，更加说明相比于普通班，实验班课程成绩波动程度较小，成绩更加稳定，各个学生之间的成绩差异并不是很大.

3 相关性分析

通过上述计算统计量的结果以及直方图显示出来的数据分布情况，我们有理由怀疑数学能力对两个班专业课成绩存在一定的影响.因此，探究专业课与数学能力之间存在的相关性，求出相关性矩阵很有必要.

从表3可以看出，在普通班上，数学能力与各科成绩相关系数均为正数，除了企业会计学2这门课相关系数较低，其他科目与數学均存在明显的正相关性，说明数学能力强的各科成绩相对就高.其中数学能力与财务管理、企业会计学、统计学、初级会计学、经济学基础和市场营销学的相关系数全都大于0.4，而在管理学，会计模拟实训，经济法这些传统的偏文科类学科上相关系数较小，可见数学能力对专业成绩的影响力较大尤其是对理学类学科.

从表4可以看出，在实验班上，除会计模拟实训外，数学能力与其他各科成绩的相关系数均为正数，说明数学能力强的各科成绩相对就高.而与会计模拟实训课的相关系数虽为负数，但非常接近0，说明数学能力与这门课相关性不大，这与我们在普通班的相关性分析结果是一致的.对比普通班发现，实验班的相关系数整体来说更大一些，相关性更强一些，数学与中级财务会计2、微观经济学、初级会计学、金融学和经济法的相关系数都大于0.45，剩余科目与数学的相关系数也都在0.2～0.4，这些都说明数学能力对专业课程成绩有明显的正向影响.

4 数学成绩与专业课综合成绩多元线性回归

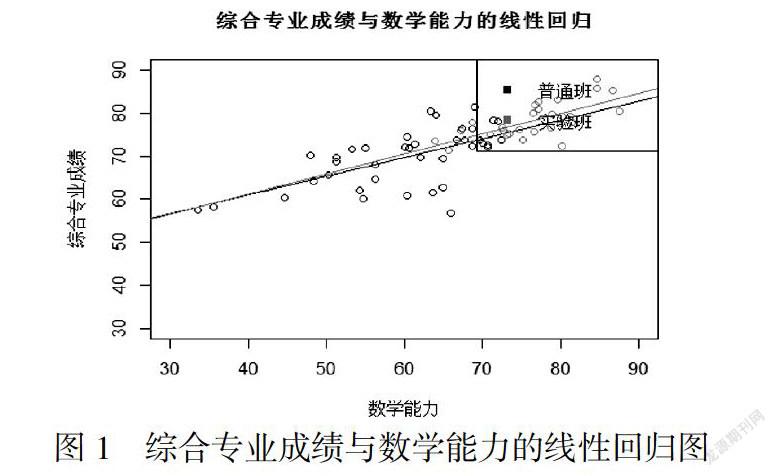
为了直观刻画数学能力对综合专业成绩的影响，接下来以每个班的数学类课程的学分进行加权计算出一个成绩来代表其数学能力，以每个班的专业类课程按照学分进行加权算出一个成绩作为专业素养成绩，将得到的数据在图1中展示出来.

从图1中大致可以看出数学能力越强，综合专业素养相对越高，二者之间存在一定的线性关系，因此建立简单线性回归分析模型.

回归方程结果如下：

此次回归结果系数均通过t检验，非常显著，但是我们发现从常数项来看实验班更低，可以说其基础成绩更低，但数学能力对其综合成绩影响更大，平均来看，数学能力每增加一分，实验班综合成绩提升将比普通班成绩提升多0.03分，而实验班数学能力整体强于普通班，所以最后呈现出来的结果就是在综合成绩上实验班强于实验班.结果表明无论对于普通班还是实验班，数学能力对综合成绩都有显著正向影响.但是从我们的回归图可以看出两个班的回归线差异不大，在尾部基本重合，所以接下来我们将利用Chow检验来说明他们影响系数之间的差异是否显著.原理如下：

H0：线性回归系数无差异？圮H1：线性回归系数有差异

计算检验统计量：

RSS是两个班数据建立线性回归的残差平方和，RSS1是普通班建立线性回归的残差平方和，RSS2是实验班建立线性回归的残差平方和.n1和n2分别是每个班的数据量，k是参数的总数.

在原假设情况下，统计量服从F分布.我们的数据进行邹检验得到的P值为0.2952849，因此我们只能接受原假设，即在两个班数学能力对综合专业成绩的影响没有统计上的差异.因此为了扩大样本量，降低统计误差，将两个班数据综合考虑建立线性回归模型如下：

y专业成绩=40.97+0.48x数学

此时建立的模型截距项和回归系数均通过t检验，非常显著，且决定系数R2为0.6205，这说明专业课成绩的62.05%可由数学能力来解释，这更加说明了在大学学习中，数学对专业课学习的重大意义.因此，从数据分析来看，数学成绩每提高一分，综合专业成绩提高0.48分，所以在大学数学类课程对我们专业课的培养有着重大意义.

5 结语

针对当前部分高校在“应用教育”的标签下，出现弱化甚至取消大学数学的倾向，我校进行教改，招募志愿者组织实验班，增加数学课程课时，优化教学内容，改革教学方法，通过实验班和普通班比较，用实验证实了，具备较丰富的数学知识和较好的数学素养是专业学习和可持续发展的重要途径，并为其它课程教学改革提供新思路.

此实验结果为学校相应专業的教学改革提出了一个新的方向——强化数学教育，使学生在大学阶段学习更多的终身受用的知识，具有可持续发展的能力.且实验结果可为同类院校教学改革提供借鉴.

——————————

参考文献：

〔1〕李明明.素质教育视阈下大学生可持续发展能力研究[J].佳木斯大学社会科学学报，2012（12）：78-79.

〔2〕高慧璇.应用多元统计分析[M].北京：北京大学出版社，2011.

〔3〕汪消银，周保平.数学建模与数学实验[M].北京：科学出版社，2015.

〔4〕盛骤，等.概率论与数理统计[M].北京：高等教育出版社，2008.2.

〔5〕张绍阁.高等数学教学与专业课程结合的探索与实践[J].教学研究，2012（4）：128-130.