发现 发展 领悟

蒋丽娟

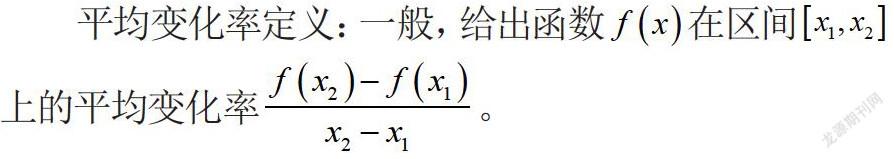
【摘 要】本文详细记述了“平均变化率”一课的教学过程。这节课的设计遵循由特殊到一般、由抽象到具体的原则，通过观察、发展、领悟这三个环节，让数学课堂成为“3D模式数学课堂”。最后总结出“3D数学课堂”教学的操作要领，并指出在教学活动中要凸显学生主体地位，以培养学生思维能力为核心，提升数学素养为目标。

【关键词】教学过程;教学反思;3D数学课堂

【中图分类号】G633.6  【文献标识码】A  【文章编号】1671-8437（2019）34-0053-02

1   基本情况

1.1  授课对象

高二物地组合普通班学生，基础较弱，但课堂氛围较活跃，善于合作交流共同探究新知。

1.2  教材分析

本节课是苏教版高中数学选修2-2第一章《导数及其应用》第一节《导数的概念》中的1.1.1《平均变化率》问题。新课标的要求是：借助生活中常见的实例分析、观察发现平均变化率，进而探究出瞬时变化率的过程，追寻导数概念的本质，明白瞬时变化率就是导数，领悟导数的思想及其内涵[1]。

1.3  教学目标

借助生活中常见的实例分析、观察发现平均变化率，进而探究出瞬时变化率的过程，追寻导数概念的本质，明白瞬时变化率就是导数，领悟导数的思想及其内涵，感悟用导数刻画世界变化的精准与奇妙。

1.4  教学重点

平均变化率的概念和意义。

1.5  教学难点

从数学的角度描述现实生活中变量变化的快慢，及如何构建平均变化率的概念。

2   教学过程

2.1 观察发现，通过问题情境发现生活中的平均变化率

变化无处不在，或细微得不易察觉，或巨大得让人惊叹！

情境1：汽车加速性能的测定，保时捷911vs法拉利360。

问题1：保时捷911速度从0增加到100公里/小时需4.1秒，而法拉利360需3.8秒，哪款车的加速性能更好？

问题2：用什么数学表达式来描述汽车速度变化的快慢？

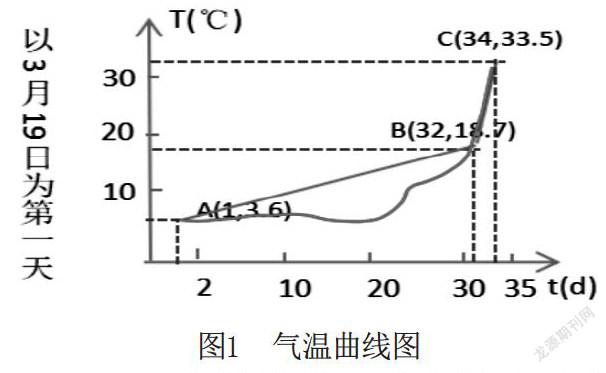
情境2：常州市2019年3、4月某几天日最高气温记载（表1）。

问题：根据上面的数据我们可以得到哪些信息？

师：4月19日到4月21日，气温忽然升高了14.8℃，人们都在惊叹：“天气热得太快了！”而3月19日到4月19日，气温增加了15.1℃，甚至超过了14.8℃，人们却不会发出上述感叹，为什么？4月19日到4月21日气温变化快——陡增！数学意义是什么？观察情境2的气温曲线图，思考以下问题：

思考1：“气温变化较快”时，图象有何特征？（视觉化）

思考2：如何量化曲线的“陡峭”程度？（数量化）

总结与思考：如何刻画变量f（x）在区间[x1，x2]上随x变化（增加或减少）的“快”与“慢”？

2.2  发展生成，根据发现归纳总结出平均变化率的具体定义

平均变化率定义：一般，给出函数在区间上的平均变化率。

根据对情境2的具体分析，师生共同归纳两点：

1）平均变化率的实际作用：反映函数变化快慢;

2）平均变化率的几何意义：割线的斜率。

回头再看前面的问题，用平均变化率来解释它们.

讨论交流：

你能举出一些用函数的平均变化率刻画因变量随自变量变化“快慢”的例子吗？

函数平均变化率的数值如何刻画因变量随自变量变化（增加或减少）的“快慢”？

2.3  领悟体验，在实际问题中研究平均变化率

例1.甲获利8万元，乙获利2万元，那么，你能评价甲、乙两人投资策略的优劣吗？变式：甲乙两人做金融投资时投入的资金相同，甲4年后获利8万元，乙在第4个月末挣到2万元，你能评价甲、乙两人投资策略的优劣吗？

例2.小宇的二胎妹妹从出生到9岁的身高变化如图所示，试分别计算从出生到3岁与6岁到9岁妹妹身高的平均变化率。

设计意图：上述两例是教材上的例题，在学生建立起平均變化率的概念之后，进行强化训练，渗透算法、算理，加深对平均变化率概念的理解，侧重于理解平均变化率的实际意义。

设计意图：让学生回顾并体会直线的斜率的含义，并发现直线的斜率与平均变化率的关系.

例4.已知函数g（x）=x3，分别计算在下列区间上的平均变化率：

设计意图：让学生感知平均变化率在不同区间上发生的变化与联系，从而找出相似之处，为后续引入瞬时变化率做好铺垫。

2.4  归纳总结，理清知识结构，增加知识储量

（1）f（x）在区间[x1，x2]随x变化的快慢可用f（x）的平均变化率来刻画.。

（2）f（x）在区间[x1，x2]上的平均变化率是曲线y=f（x）在区间[x1，x2]上变化趋势的代数刻画，曲线变化趋势是平均变化率的直观感知。

（3）f（x）在区间[x1，x2]上的平均变化率是在其局部区间上f（x）随x变化的快慢以及曲线y=f（x）陡峭程度的一种粗略刻画。

3   教学反思

在教学过程中还存在简单化处理简单概念的问题，没有充分的时间让学生在课堂上大展身手。在引导过程中思维过于局限、不开阔、快人快语，要把发现新知的机会抛给学生[2]。即使他们绕了点弯路，并没有在两次尝试后给出平均变化率的本质含义，只要大方向不错，不要着急去纠正他们，要让他们通过自己思考总结出来，这样学生会十分有成就感，容易激发数学学习兴趣。另外，在后续概念应用环节，练大于想，应该让学生多感受一些特殊曲线的平均变化率，不要局限于熟悉的一次二次三次函数，思维要开阔。对整体的把握还是到位的，也做好了前后呼应，并为后续学习埋下伏笔，从学生的表现来看，大部分人都认识到了平均变化率的极端情况就是瞬时变化率，为后续学习导数打下很好的基础。

【参考文献】

[1]殷堰工.教材是开展高中数学探究性学习的重要资源[J].中学数学月刊，2011（5）.

[2]王建平.高中数学概念的教学模式研究[J].小作家选刊：教学交流，2012（8）.