利用导数求极值的新解法探索
2019-09-10方旅君
新教育论坛 2019年34期
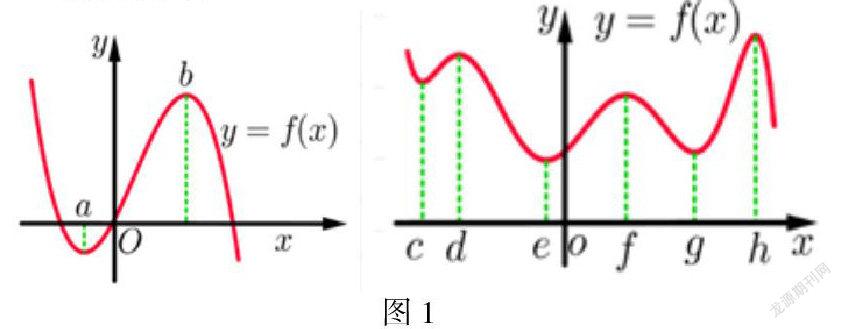
摘要:传统教材出现的利用导数求极值,有一定难度,这里尝试用新方法求极值降低学习难度
关键词:函数;导数;极值;求解
传统教材中利用导数求极值的方法,对于职业高中学生来讲,还是有一定难度,这里尝试用新方法求极值,目的让职高学生能降低学习难度,也让普高學生丰富解题路径。
一.传统教材利用导数求极值的依据及步骤
1.极值的概念
三.新方法求极值的特点及作用
1知识点更简明
传统教材判定极值的第三个步骤,需要用到不等式知识,以及记住极值处附近导数的判定法则,比较复杂。新方法第三步,只要在相邻两个极值区域内任取f(x),与极值比较大小即可。新方法第三步只有比较数值大小一个知识点,故理论更简明。
2计算会更方便
因为利用新方法求极值时,当求出极值点处的极值后,可以任意取一个容易计算的数值x0代入原函数中,求出f(x0),与极值点处的极值进行比较,来确定极值点处的极值是极大还是极小值。故应用知识点变少,计算难度降低;对于不需要严密求证的选择题,填空题,解题速度更快,所以新方法计算更方便。
3新方法求极值的用途
利用新方法求导数,避开不等式求解,以及极值判断法则,这样能帮助不等式知识掌握不好的学生,以及思维能力较差,计算能力较弱的学生,很好地去解决极值求解问题。故适用职高学生去学习掌握,对普高学生来说多掌握一种解题途径能提高解题速度。
参考文献:
[1]数学及解题指导 (人民教育出版社中学数学室编)
作者简介:方旅君(1969.02-),男,汉族,浙江余姚,高级教师。
