生活中的三角函数

陈伟斌

在实际生活中，有许多周期现象，如日出日落、阴晴圆缺、四季轮回、潮起潮落;又如心脏的收缩和舒张，甚至是人的情绪、体力……那么用来描述周期现象最基本最重要的函数义是什么呢？当然是三角函数！下面我们来看几个案例，体会三角函数在生活中的应用.

案例1 聪明的船长

若干年后，阅读本文的某位读者成为了船长，有一天船要到某个港口去，作为船长，港口的水深与时间的对应关系是他最迫切需要知道的信息.

下面是某个港口的码头在今年春季每天的时间与水深的关系表：

（1）请你仔细观察表格中的数据，你能够从中得到一些什么信息？

（2） -艘货船的吃水深度（船底与水面的距离）为4m，安全条例规定至少要有1.5 m的安全间隙（船底与洋底的距离），试问：该船何时能够进入港口？在港口能待多久？

（3）在（2）的条件中，若该船在2：00开始卸货，吃水深度以0.3 m/h的速度减少，那么该船在什么时间必须停止卸货，将船驶向较深的水域？

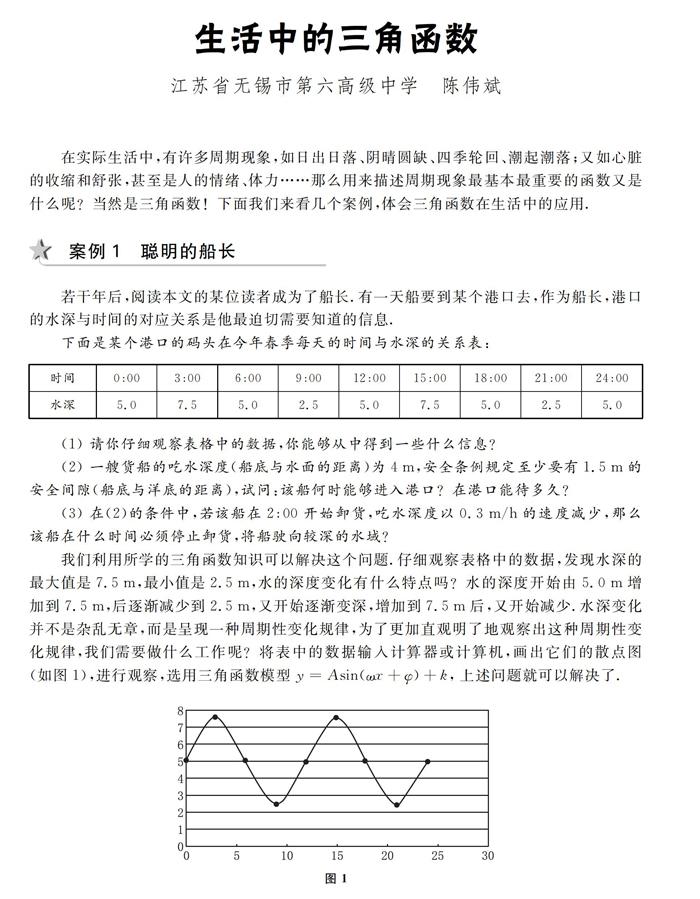
我们利用所学的三角函数知识可以解决这个问题.仔细观察表格中的数据，发现水深的最大值是7.5 m，最小值是2.5 m，水的深度变化有什么特点吗？水的深度开始由5.O m增加到7.5 m，后逐渐减少到2.5 m，义开始逐渐变深，增加到7.5m后，义开始减少.水深变化并不是杂乱无章，而是呈现一种周期性变化规律，为了更加直观明了地觀察出这种周期性变化规律，我们需要做什么工作呢？将表中的数据输入计算器或计算机，画出它们的散点图（如图1），进行观察，选用三角函数模型y=Asin（ωx+Φ）+k，上述问题就可以解决了.

案例2 感受你的心跳

在这个重视个人健康问题的社会，懂一点点生理知识对每个人都是大有好处的.

心脏跳动时，血压在增加或减小.血压的最大值、最小值分别称为收缩压和舒张压，血压计上的读数就是收缩压和舒张压，读数120/80 mmHg（注：1 mmHg=133. 28 Pa）为标准值.设某人的血压满足函数式p（t）=110+25sin（1607πt），其中p（t）为血压（mmHg），t为时间（min）.（1）此人的血压在血压计上的读数为___ ;（2）每分钟心跳次数为___.

第（1）小问先根据函数p（t）=110+25sin（160t）求出最大值135和最小值85，进而可得到收缩压为135和舒张压为85，故答案为135/85.

第（2）小问的频率就是每分钟心跳的次数，因为T=2π/160π一1/80，所以此人每分钟心跳次数为1/T=80次.

案例3 船有触礁的危险吗

海中有一个小岛A，该岛四周1O km内有暗礁.今有货轮由西向东航行，开始在A岛南偏西55°的B处，往东行驶20 km后，到达该岛的南偏西25°的C处，之后，货轮继续往东航行，你认为货轮继续向东航行途中会有触礁的危险吗？

在Rt△ABD和Rt△ACD中，AD是它们的公共直角边.而且BC是这两个直角三角形BD与CD的差，即BC—BD CD.BD，CD的对角是已知的，BD，CD和边AD都有联系.

在Rt△ABD中，tan 55°=BD/AD，BD=ADtan 55°;在Rt△ACD中，tan 25=CD/AD，CD=ADtan 25°，利用BC=BD=CD就可以列出关于AD的一元一次方程，即ADtan 55°ADtan 25°=20.最后测算m AD与1 0的大小关系，即可解决问题.

在实际生活中，还有许多周期现象可以用三角函数来模拟，如力学中的简谐振动、交流电中的电流等，都可以建立三角函数的模型利用三角函数的性质解决有关问题;很多最值问题也可以转化为三角函数来解决，如天气预报、建筑设计、航海、航天等都能找到三角函数的影子.三角函数与我们的生活息息相关，应用极广，因此我们要学好三角函数。