Chebyshev算子矩阵求解分数阶微分方程的数值解

杨晓丽 许 雷

（1 内江师范学院生命科学学院；2 内江师范学院数学与信息科学学院 四川内江 641199）

分数阶微积分是常微分和积分到任意阶的推广。与整数阶相比，分数阶微分方程在物理现象的模拟上有许多优势[1]。近几十年来，分数偏微分方程被广泛用于描述工程过程和动力学系统。越来越多的研究人员致力于研究求解分数微分方程以及解的存在性和唯一性。由于分数阶微分算子具有全局性以及对偶算子不是其负算子的性质，很难对分数阶微分方程进行求解，因此很多学者对分数阶问题的数值方法进行了研究。针对不同类型的方程提出了不同数值方法。常用的方法包括有限差分方法[2]，有限元方法[3]，谱Galerkin方法[4]以及正交多项式的方法。常用的多项式方法有Legendre多项式[5]、Chebyshev多项式[6]、Bernstein多项式[7]，以及Bernoulli多项式[8]。目前用Bernoulli多项式求解分数阶微分方程的文献很少，且运算较为复杂，因此基于分数阶微分算子矩阵的方法，引入Chebyshev多项式，结合tau法和配方法将分数阶微分方程转化为线性或者非线性方程组，以降低问题的复杂性。

一、预备知识

（一）Caputo意义下的分数阶微分[9]

定义1：Caputo类型的分数阶微分定义

其中，α＞0，n是比α大的最小的整数，对于Caputo微分有DαC=0，C为常数

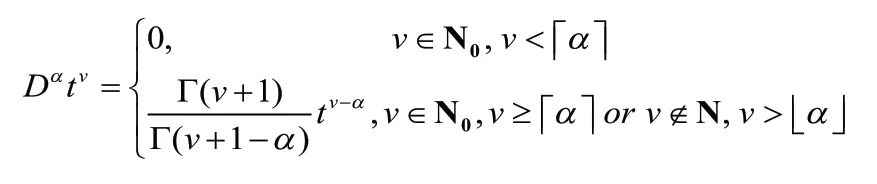
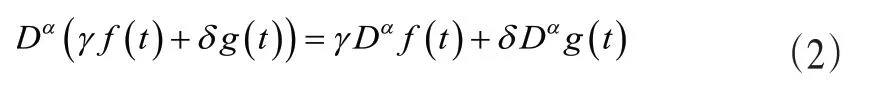
其中，γ和δ为常数。

（二）Chebyshev多项式的性质[10]

定义2：定义在[-1,1]上的Chebyshev 多项式为可由如下递推公式得到：

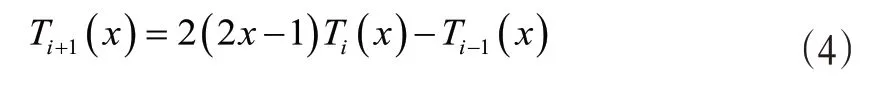
移位Chebyshev多项式的解析解表示为：

满足如下正交性：

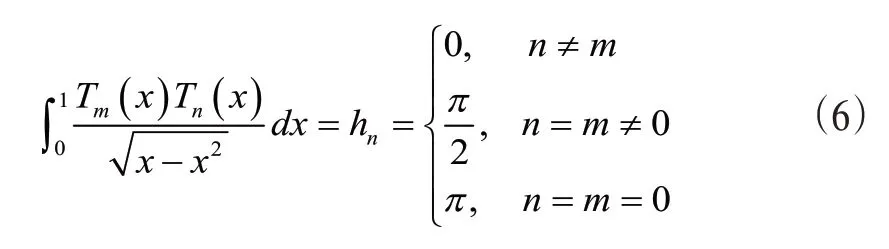
（三）Chebyshev 多项式函数逼近。设H=L2([0,1])Chebyshev多项式集合，γ=则对于H空间中的任意函数存在唯一的最佳近似g(t)∈γ：

式（7）等价于

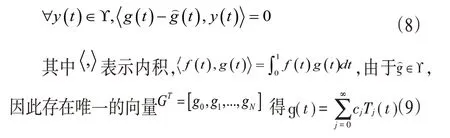
其中，系数可以由如下公式得到，

在实践中，只用前N+1项，即

二、分数阶微分的Chebyshev算子矩阵

利用公式（12）得到，

引理1：设Chebyshev多项式，则

引理1 利用Caputo 微分的定义和公式（5）很容易证明，在此略。

定理1：设为移位Chebyshev向量，v＞0，

其中，D(v)为维的在caputo 意义上的分数阶微分的运算矩阵，定义如下：

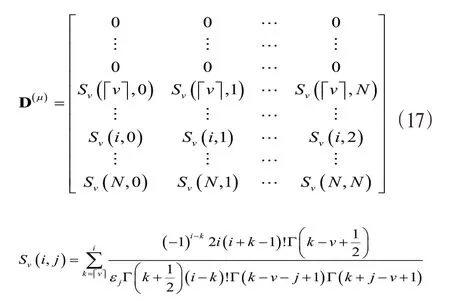
证明：

利用N+1项Chebyshev多项式逼近tk-v，得到

整理公式（18）（19）就可以得到证明的结果

三、数值计算方法

（一）线性分数阶微分方程的求解。考虑Caputo意义下的分数阶微分方程具有如下的形式：

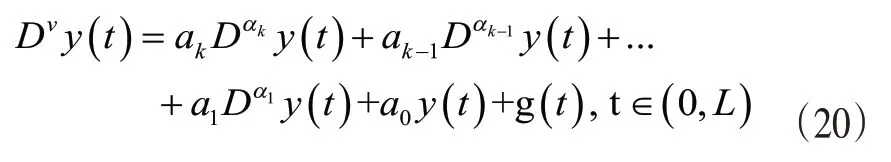
初始条件满足：

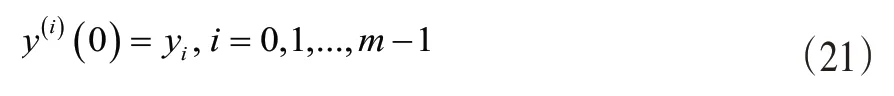
利用Chebyshev多项式可以将y(t)和ɡ(t)近似为：

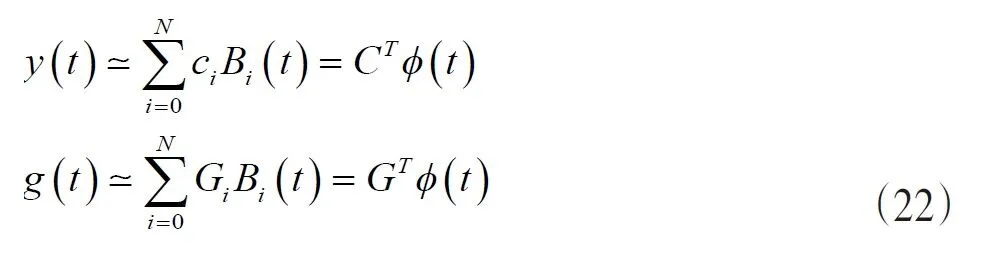
其中，向量G可以由公式（10）求得，为未知向量，根据定理1，分数阶微分可以做如下近似：

因此，公式（14）的残差R(t)可以表示为：

利用经典的Tau方法，我们可以利用如下公式产生维的N-m+1线性方程组：

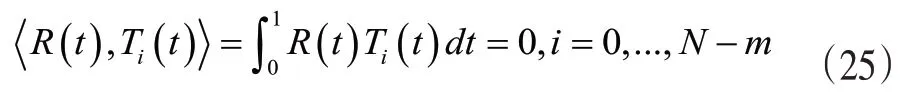
利用初始条件可以得到，

（二）非线性分数阶微分方程的求解。对于如下的非线性分数阶微分方程：

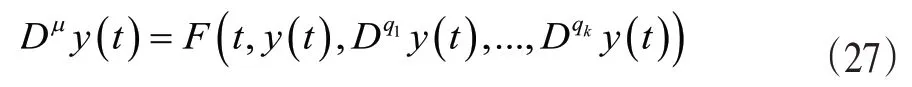
初始条件如（21）式,0＜q1＜…＜qk＜μ，则y(t),Dμy(t)，以及Dq jy(t)的近似处理和线性方程一样，因此可以得到，

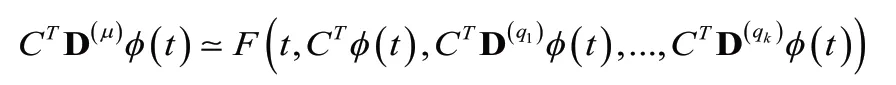
在配置点上，上述公式是完全相等的，因此选择为N-m+1移位勒让德多项式的根为配置点联合初始条件得到N+1维的非线性方程组，利用典型的迭代方法，如牛顿迭代方法就能得到的近似解。

四、实例计算

例1：考虑如下非线性初值问题[11],

精确解为y(t)=t2

假设N=2，则方程的解可近似为：

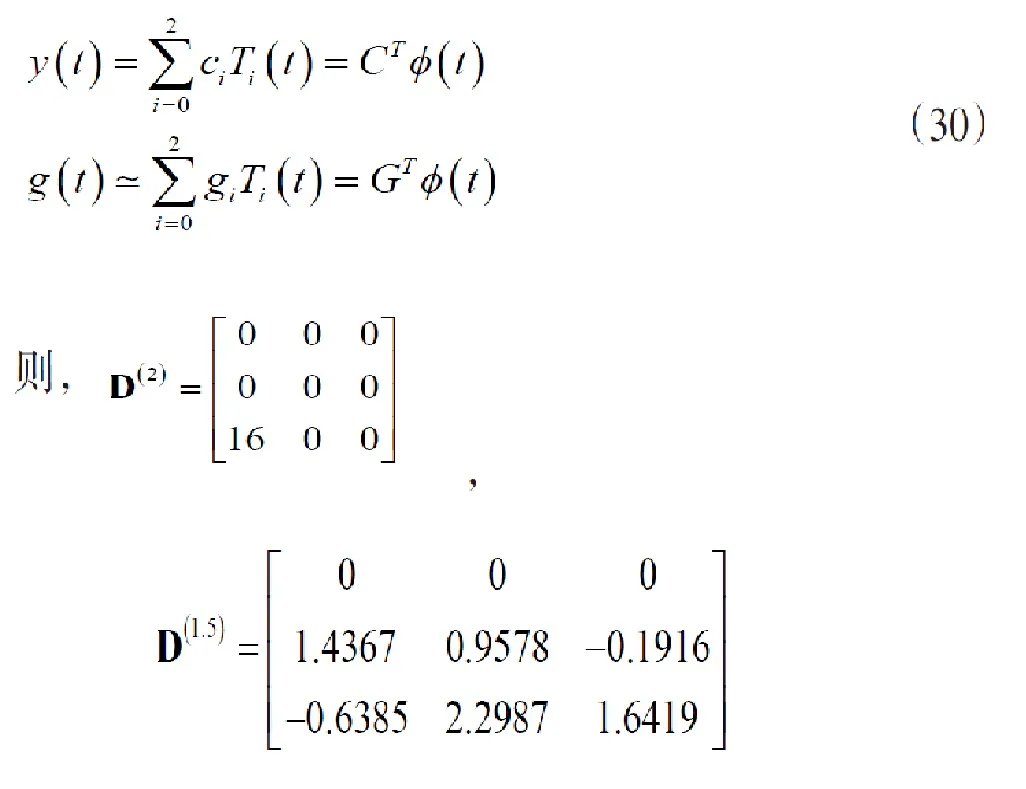
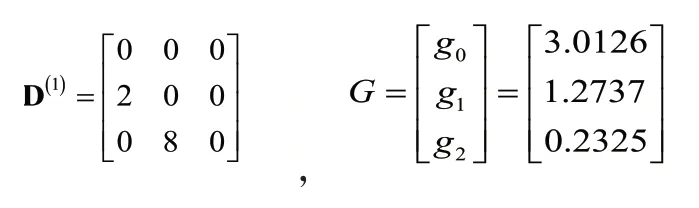
因此可以得到线性方程组：

解得CT=[0.375 0.5 0.125]

例2：考虑如下边界Bagely-Torvik问题[12],

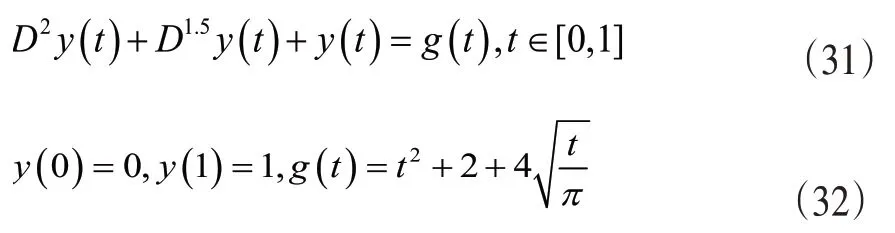
上述方程有精确解y(t)=t2

假设N=2，则方程的解可近似为：

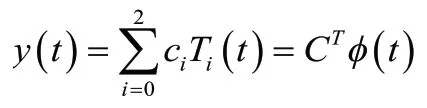
对边界条件进行处理得：

因此，利用3.1节的方法，同样可以得到

五、结论

文本提出了解决一类分数阶微分方程的Chebyshev矩阵方法。基于L2空间下，任意函数可由Chebyshev 多项式张开，将分数阶的微分方法转化为线性或者非线性方程组进行求解，降低了方程的计算复杂性，并通过实例分析证明了算法的有效性。