基于道路环境因素的公路隧道交通事故预测

王 蕾， 邱 锋, 2， 夏永旭， 韩兴博

(1. 长安大学公路学院， 陕西 西安 710064； 2. 陕西碧桂园置业有限公司， 陕西 西安 710065)

0 引言

公路隧道的快速发展给我们带来了显著的经济与社会效益，然而由于其结构的封闭性与复杂性，导致运营安全方面存在很大的潜在威胁。尤其随着长隧道和特长隧道的不断增加，隧道路段已成为交通事故的高发路段[1]，且一旦发生事故，其严重程度和致死率远高于普通路段。因此，研究公路隧道交通安全，特别是交通事故的预测，对公路隧道交通安全管理工作具有非常重要的现实意义。

近年来，国内外许多学者对公路隧道交通安全问题进行了研究，并取得了一定的成果[2-6]，但这些研究多以对事故结果的统计分析为主。后续，也有学者关注公路隧道交通事故的预测工作。易富君等[7]构建了基于遗传算法优化的RBF神经网络模型，并提出了公路隧道群交通事故的微观预测方法； 段萌萌等[8]研究了高桥隧比高速公路交通事故的影响因素及规律，采用多元非线性回归分析法建立了事故预测模型； 马壮林等[9]采用有序Logit模型和广义有序Logit模型对交通事故严重程度进行了预测； Ciro等[10]以200余起公路隧道交通事故数据为基础，采用随机参数方法建立了事故频率预测模型； 詹伟等[11]结合事故灰色预测模型与马尔可夫模型，分析了隧道群路段交通事故的发展变化趋势； 杨健等[12]以沈海高速罗长隧道群为研究对象，建立了基于BP神经网络的交通事故非线性综合预测方法。

总结上述研究发现，目前的公路隧道交通事故研究多以统计分析为主，有关事故预测的研究相对较少，且影响因素考虑不全面，基于道路环境影响因素的事故预测研究更是几近于无。本文以秦岭某隧道群事故统计资料为基础，拟通过相关性分析对影响公路隧道交通事故预测的道路环境因素进行主要变量筛选，同时采用朴素贝叶斯模型、随机森林模型、BP神经网络模型和支持向量机模型分别对公路隧道交通事故形态、严重程度、伤亡情况和持续时间进行预测，以期能在进行不同类别事故预测时选取合适的预测模型，并为今后的公路隧道交通事故预测工作提供一定的参考。

1 预测方法

交通事故的发生是诸多因素综合作用的结果，当其发生在公路隧道中时更显复杂，为了得到相对准确的预测结果，预测方法的选择尤为重要，如果选择不合适的预测方法，结果将差之千里。下文将对几个常用的预测模型进行分析研究。

1.1 朴素贝叶斯模型

朴素贝叶斯模型是在各特征属性条件独立的基础上基于贝叶斯公式所建立的一种智能算法。其基本思路是通过先验概率得到后验概率，即交通事故的预测可以通过各影响因素发生的概率计算得到，文献[13]详细介绍了朴素贝叶斯模型的基本原理及算法步骤。

朴素贝叶斯模型算法简单，对小样本量数据预测较为准确。其缺点在于其条件独立性假设较难满足，并且会因为先验概率的不准确导致预测效果不佳。

1.2 BP神经网络模型

BP神经网络模型是一种多层网络模型，由输入层、隐层、输出层3层构成，网络结构如图1所示。其算法过程由正向的结果输出和反向的误差调整构成，若数据经过正向输出所得结果误差较大，则反向传播预测误差调节隐含层神经元，重复此过程直到误差满足要求[14]。

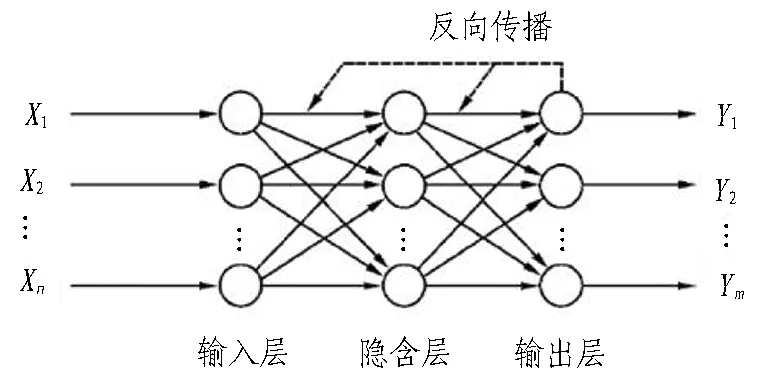
图1 BP神经网络结构图

BP神经网络模型非线性映射能力较强且具有较强的容错能力，但由于其收敛速度慢导致算法低效，也有可能陷入局部极值而得不到最优结果。

1.3 随机森林模型

随机森林模型是由很多决策树分类模型组成的组合分类模型，通过有放回地随机抽样组成决策树，然后组合多棵决策树的预测，通过投票得出最终的预测结果，其构建过程如图2所示。

图2 随机森林模型结构图[15]

随机森林模型预测准确度较高，不容易出现过拟合的现象，然而当样本量较小时，随机森林模型的不完全抽取可能会使得所抽取数据没有代表性。

1.4 支持向量机模型

支持向量机模型是基于结构风险最小化所建立的数据模型，具体原理在文献[16]中有详细介绍。它的优点在于结构简单、适应性好、泛化能力强，但由于缺乏相关依据使得核函数的选择较为困难，数据中特殊点的存在也会对结果造成一定影响。

2 预测指标

2.1 自变量选取

交通事故影响因素涉及人、车、道路环境3大方面，本文拟着重研究道路环境因素对公路隧道交通事故的影响。结合前人研究成果及西汉高速秦岭隧道群的调查统计资料，选取相关影响因素作为特征变量，如表1所示。

2.2 相关性分析

为降低计算成本与难度，对上述自变量进行相关性分析，以筛选出相关性较高且对预测结果具有显著影响的自变量参数。本文采用的是皮尔森相关性系数法，计算公式如下：

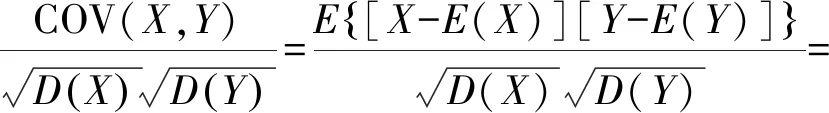
(1)

式中：ρXY为自变量X对因变量Y的相关性系数； COV(X,Y)为变量X与变量Y的协方差；D(·)为变量的方差；E(·)为变量的数学期望。

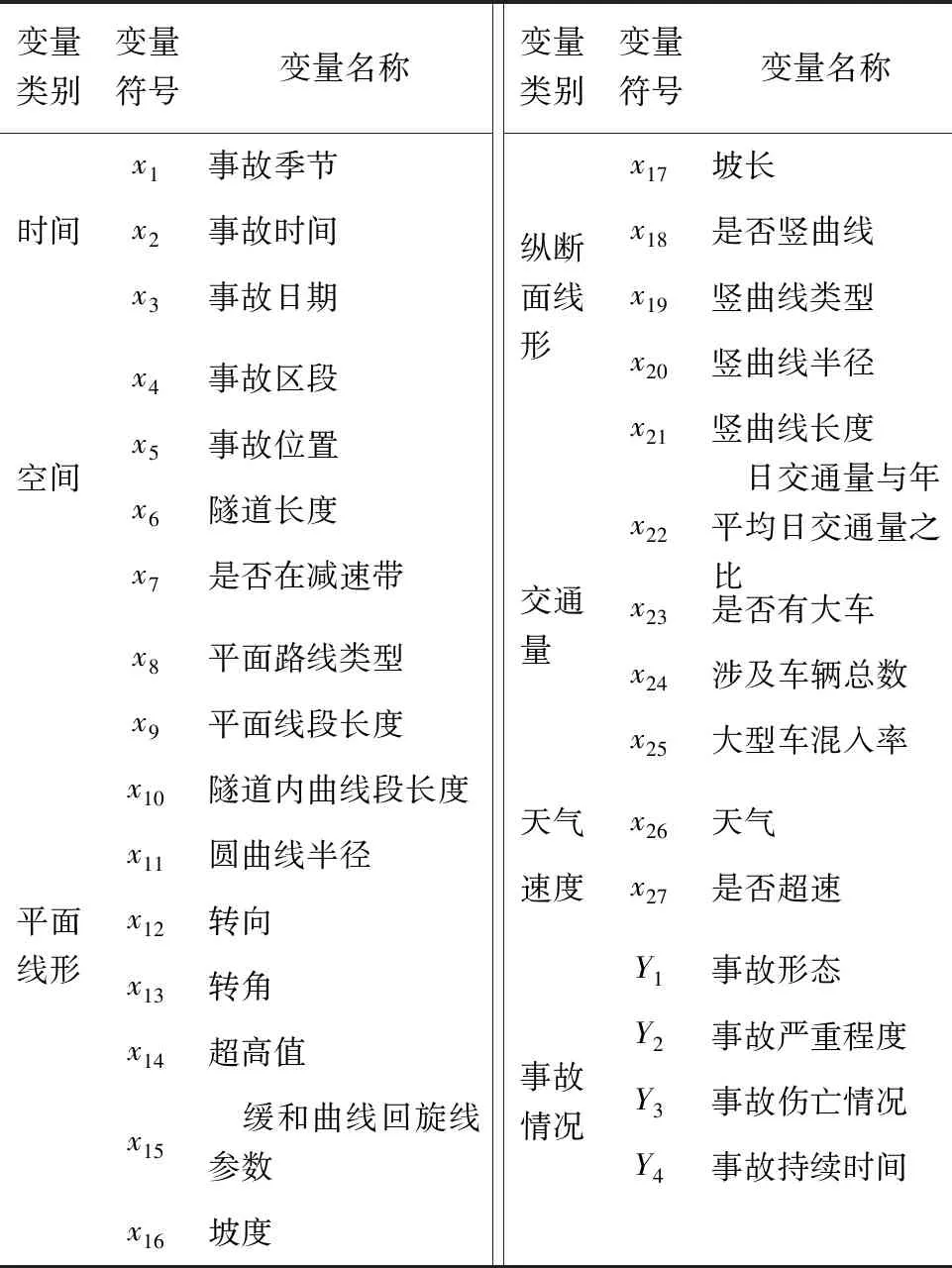
表1 变量描述表

分别以事故形态、事故严重程度、事故伤亡情况和事故持续时间作为因变量，通过皮尔森相关性分析计算各自变量的相关系数，选取9个最大系数的自变量，对其进行编码赋值后将其纳入到预测模型之中，筛选结果如表2所示。

3 预测模型比选

本文以西汉高速秦岭某隧道群的交通事故为研究对象，西汉高速秦岭段具有交通量大、隧道数量多、线形复杂、事故频发等特点，全线共有130座隧道，隧道总长约110 km，本文所选取的隧道群处于事故多发路段，其设计速度为80 km/h，均为双洞分离式隧道，事故数据采集时间为2014年8月至2017年底，共计496起事故，具体分布如表3所示。以上述事故数据为样本，将筛选的4组36个自变量作为模型参数，采用不同模型分别对事故形态、严重程度、伤亡情况和持续时间进行预测。

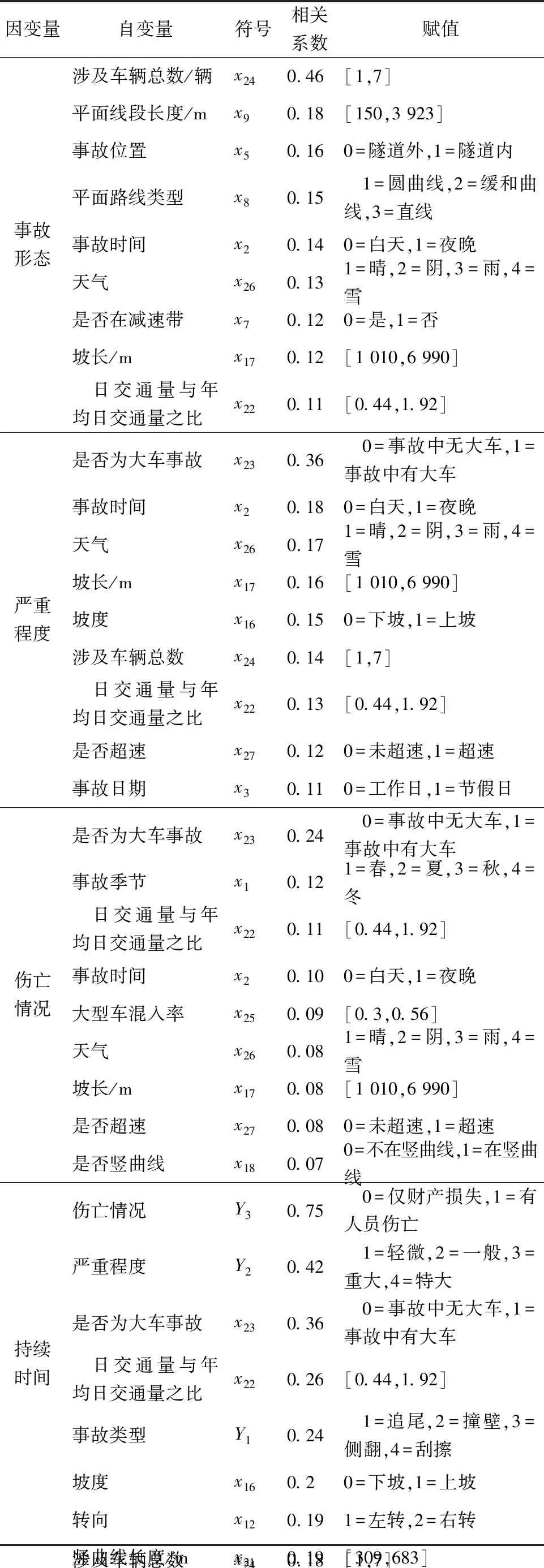
表2 自变量筛选及赋值

表3秦岭公路隧道交通事故统计数据

Table 3 Statistical data of traffic accidents of Qinling Highway Tunnel group

年份交通事故数20143520151012016208201752

3.1 交通事故形态预测

采用Matlab随机函数将收集到的496起事故数据随机分为2部分，依次作为训练集和测试集，对数据进行反复迭代得出预测准确率，连续5次运行模型程序，取其平均值作为最终准确率，以预测结果的准确率对不同模型进行评价。准确率计算公式如下：

(2)

式中： accuracy为模型预测准确率； length(predict=text label)为预测准确个数； length(text label)为训练集个数。

3.1.1 朴素贝叶斯模型

采用贝叶斯模型分别计算各事故形态的发生概率，选择最高概率结果所对应的形态作为预测结果，并与实际事故形态进行对比，计算预测准确率。部分贝叶斯模型事故形态预测结果如表4所示。

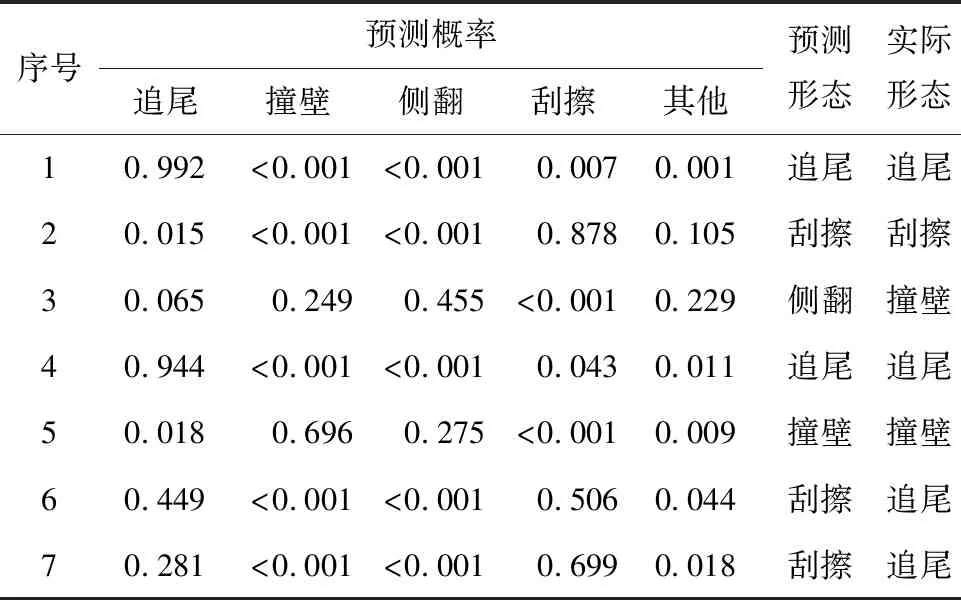
表4 贝叶斯模型事故形态预测结果

根据调查数据进行多次预测，计算得到朴素贝叶斯模型的预测准确率约为69%，标准差为0.92。

3.1.2 BP神经网络模型

针对模型中的多项分类，激活函数选取Softmax函数，迭代次数设为30 000次，学习率为0.01，隐含层节点数为5，连续多次运行BP神经网络模型程序，准确率见图3。可知，模型的预测准确率平均值约为82.09%，标准差为1.38，模型训练时间约为1 min。

3.1.3 随机森林模型和支持向量机模型

将前文所选特征向量纳入随机森林模型和支持向量机模型，连续多次运行模型，预测准确率如图4所示。随机森林模型的预测准确率平均值约为84%，标准差为0.29； 支持向量机模型的预测准确率平均值约为71%，标准差为0.61。

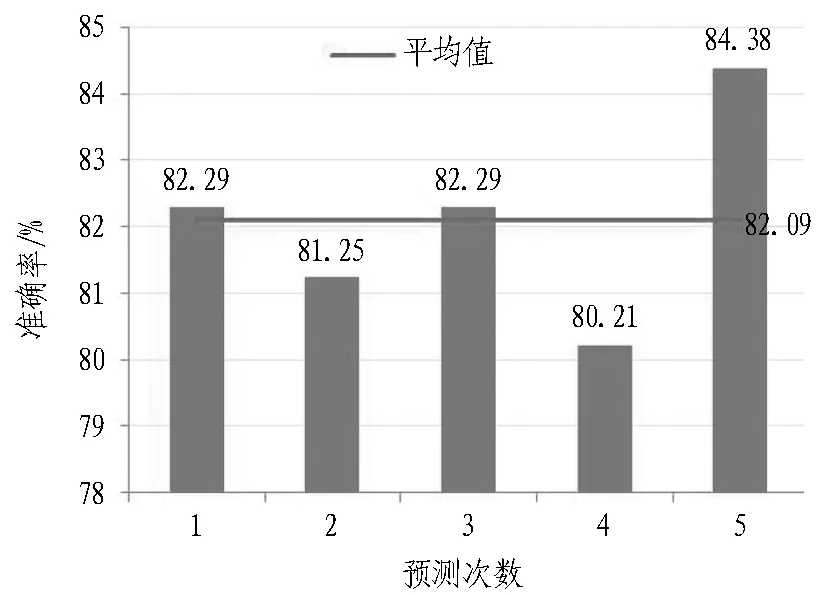
图3 BP神经网络模型事故形态预测准确率

Fig. 3 Prediction accuracy of accident form by BP neural network model

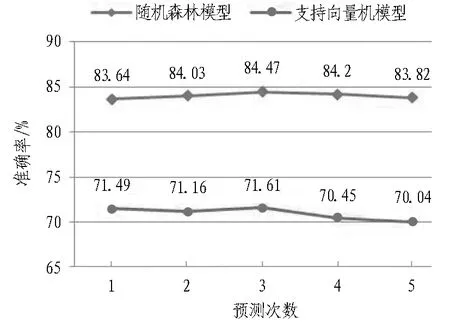
图4 随机森林模型和支持向量机模型事故形态预测准确率

Fig. 4 Prediction accuracy of accident form by random forest model and support vector machine model

将以上模型进行对比分析，综合考虑预测模型的准确率与稳定性，不难看出随机森林模型最适合对公路隧道交通事故形态进行预测。

3.2 交通事故严重程度预测

公路隧道交通事故严重程度的准确预测对快速救援与交通疏导意义重大，对于损失巨大且伤亡惨重的重大及特大交通事故的预测一直都是预测工作的重中之重，在进行模型选择时需重点考虑大型事故预测的准确程度。参照我国《道路交通事故处理办法》及公安部颁布的交通事故分类方法，将事故严重程度分为4类，如表5所示。预测模型训练集与测试集的构建与前文相同，不同模型预测准确率结果统计如表6所示。

由表6可知： 随机森林模型在预测轻微事故时准确率最高，但对一般、重大和特大事故的预测较为困难。贝叶斯模型在预测轻微事故时准确率虽不及其他模型，但其对一般和重大事故的预测准确率较高，而且贝叶斯模型对小样本量数据的预测较为擅长。因此，在进行公路隧道交通事故严重程度预测时可优先考虑贝叶斯模型。

表5 事故严重程度分类

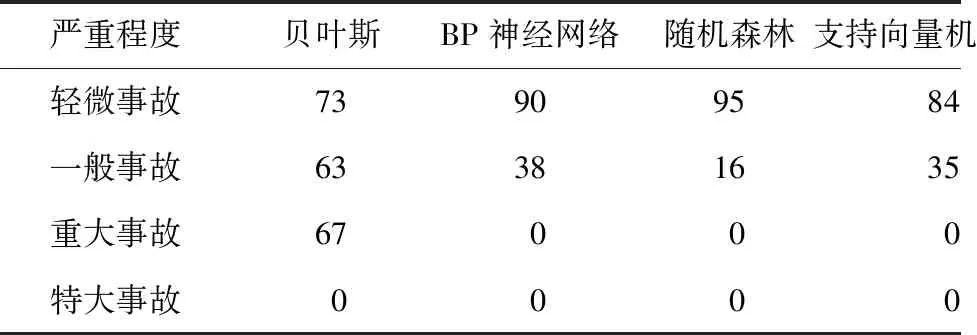
表6 不同模型事故严重程度预测准确率

3.3 交通事故伤亡情况预测

采用4大智能模型分别对伤亡情况进行预测，预测准确率结果统计如表7所示。由于伤亡事故数据样本量较小，模型在运行时表现稍显不佳，准确率相对较低。其中，BP神经网络模型共预测到6次伤亡事故，准确率为50%，但结合实际发生的32起伤亡事故，其预测成功率仅为9%；贝叶斯模型的准确率虽然较低，但预测成功率达到了40%，考虑伤亡最小化原则，选择贝叶斯模型作为公路隧道交通事故伤亡情况预测模型。

3.4 交通事故持续时间预测

交通事故持续时间指的是从交通事故发生到交通恢复正常的总时间，可划分为事故检测响应阶段、事故清除阶段及交通恢复阶段3个阶段，通常采用事故响应处理时间与拥堵消散时间2个指标来描述事故路段拥堵的时间影响。拥堵持续时间即为事故响应处理时间与拥堵消散时间之和[14]，因此，本文采用拥堵持续时间代替交通事故持续时间作为因变量。

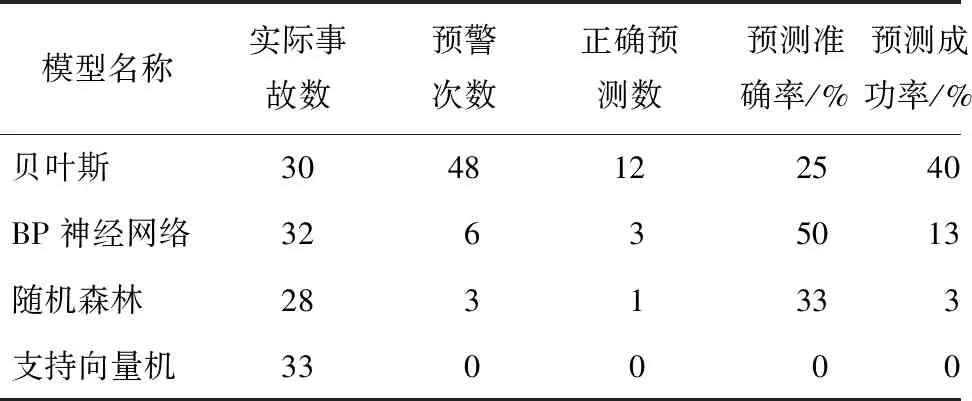
表7 不同模型事故伤亡情况预测准确率

图5为BP神经网络模型对事故持续时间的预测结果图。可以看出，预测值与实际值的起伏趋势大致相似，20～50 min期间的预测值相对较为准确，而其他时间段预测值误差极大。

图5 BP神经网络模型事故持续时间预测结果

Fig. 5 Prediction results of accident duration by BP neural network model

图6为随机森林模型对事故持续时间的预测结果图。可以明显看出，预测值和实际值的吻合程度较高，特别是持续时间较长时，预测结果误差依旧较小。

图6 随机森林模型事故持续时间预测结果

Fig. 6 Prediction results of accident duration by random forest model

图7为支持向量机模型对事故持续时间的预测结果图。图中预测结果误差明显过大，不予考虑。BP神经网络模型和随机森林模型的预测准确率对比结果如图8所示。可见，随机森林模型最适宜于对交通持续时间进行预测。

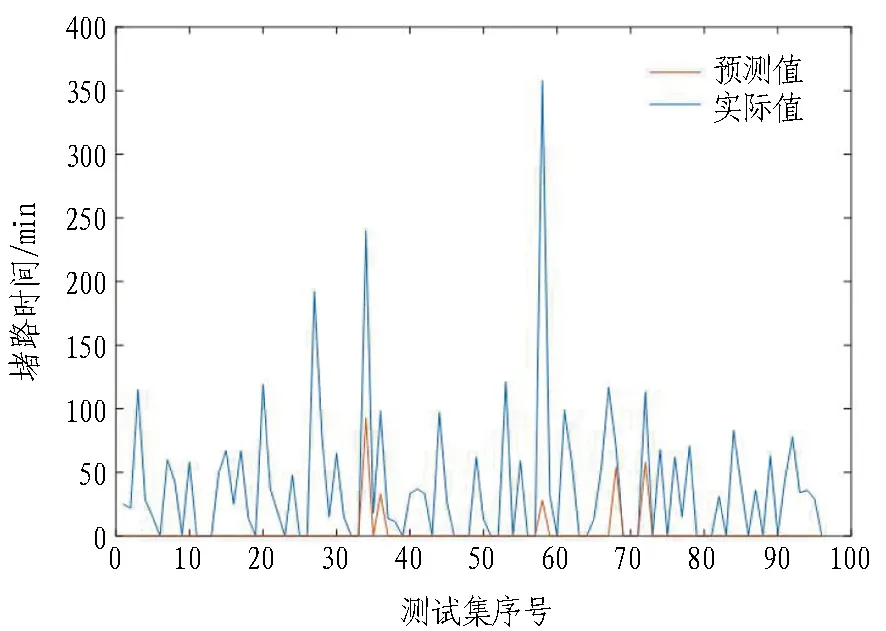
图7 支持向量机模型事故持续时间预测结果

Fig. 7 Prediction results of accident duration by support vector machine model

图8 BP神经网络模型和随机森林模型事故持续时间预测准确率

Fig. 8 Prediction accuracy of accident duration by BP neural network model and random forest model

4 结论与建议

1)随机森林模型在预测公路隧道交通事故形态时最为可靠，准确率约为84%；

2)贝叶斯模型对重大或特大事故的预测准确率高达50%，在对公路隧道交通事故严重程度和伤亡情况进行预测时可优先考虑；

3)使用随机森林模型预测公路隧道交通事故持续时间，绝对误差为20 min时模型准确率将超过70%；

4)由于事故数据的局限性，在进行伤亡情况预测时模型表现不佳，今后工作中应尽可能开展数量更多、区域更广、持续时间更长的数据搜集工作。