四象限脉冲整流器模型预测电流控制算法研究
2019-09-10陈天宇宋术全卜丽东程相勋
陈天宇, 宋术全, 卜丽东, 程相勋
(1 中车长春轨道客车股份有限公司, 长春 130062;2 中国铁道科学研究院集团有限公司 机车车辆研究所, 北京 100081;3 北京纵横机电科技有限公司, 北京 100094;4 郑州地铁集团有限公司, 郑州 450046)
四象限脉冲整流器(Four-quadrant Converter, 4QC)作为机车车辆的主要供电电源装置,在我国轨道交通领域得到了广泛的应用[1-2]。四象限脉冲整流器控制技术决定了牵引系统的控制性能, 成为国内外学者的研究热点。
通过控制4QC网侧电流的相位,可使牵引变流器整体对外显现为纯电阻特性,即实现了单位功率因数控制的功能。通过控制4QC电流幅值,可实现对直流侧电压的调节,进而可为后级逆变环节提供稳定的供电电压[3-4]。
瞬态直接电流控制(Transient Current Control, TCC)实现较为简单,但由于其电流内环仅采用比例控制器而未采用积分控制器,因而无法实现稳态下网侧电流的无残差控制。dq轴电流解耦控制将网侧电流进行解耦,并将其变换为直流量,便于利用PI调节器进行高性能控制,同时简化了系统模型。但是该方法的关键是对PI控制参数进行优化,其设计难度较大。比例谐振(PR)控制[9]的优点是稳态精度较高,但是,当网侧供电频率波动时,其控制精度将明显降低。此外,在实际工况中通常需要并联多个PR控制器以提高控制精度,这将导致控制系统复杂,稳定性能降低。间接电流控制[10]仅通过一个PI调节器对直流母线电压进行控制从而达到间接控制网侧电流的目的。该方法实现较为简单,稳定性较高,但是无法实现对网侧输入电流的高精度控制。
模型预测电流控制(model predictive current control, MPCC)分为有限集(finite-control-set, FCS) MPCC和连续集(continue-control-set, CCS) MPCC两类。传统FCS-MPCC算法建立的高采样频率和较强的运算性能的基础上,虽然该方法能实现较高的控制性能,但由于该控制方法开关频率不固定,容易造成较高电流波动。文献[6]提出了一种直接功率模型预测控制方法,该方法具有较快的动态响应能力,但是其开关频率无法固定。文献[7]提出了一种定开关频率的预测控制方法,提高了的工程实用性。文献[8]将占空比最优作为调节目标,通过构建评价函数实现了有效电压矢量作用的最优化,提高了控制动态和稳态性能。
以4QC为研究对象,首先建立了4QC的数学模型,构建了评价函数,分析了一种连续集(continue-control-set, CCS)模型电流控制CCS-MPCC的算法原理。通过试验证明了MPCC算法的有效性。
1 4QC数学模型
根据图1所示的拓扑结构,4QC电压方程可以表示为
(1)
2 瞬态直接电流控制
TCC算法包含内环PI调节器和外环比例调节器两部分,其原理图如图 2所示,其原理表达式为
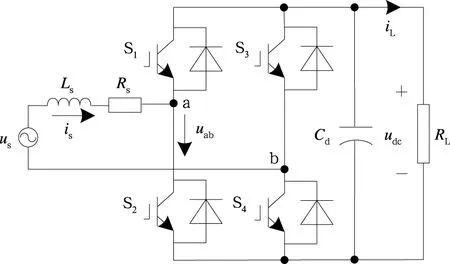
图1 4QC结构图
(2)
式中,外环PI调节器实现了对直流电压的控制,内环比例调节器实现了对输出电压指令的控制。Udc*为直流侧电压给定值;Ism*为交流侧电流峰值的给定值。

图2 TCC控制原理图
由式(2)及图 2可知,电压外环PI调节器可以使直流电压反馈值udc跟踪电压给定值Udc*,并输出交流电流给定值Ism*的动态分量Ism1*。交流电流给定值的稳态分量Ism2*作为电流指令的前馈量,可提高控制的响应能力。
3 模型预测电流控制
3.1 二阶广义积分算法
采用二阶广义积分方法(second-order generalized integral,SOGI)构建虚拟坐标系,如式(3)所示。
(3)
式中,k为阻尼系数。其框图如图 3所示。
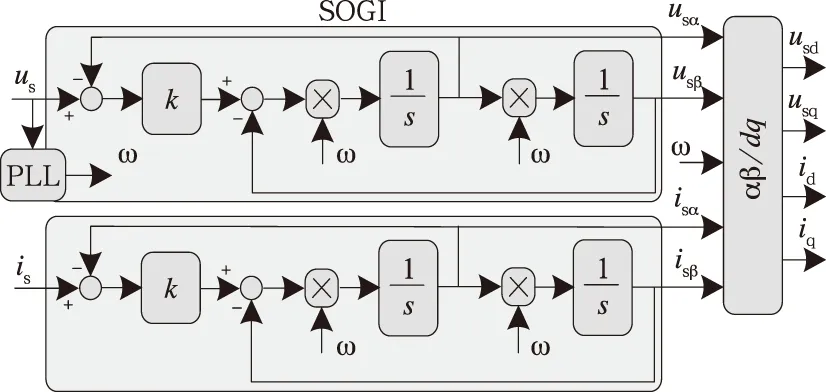
图3 SOGI结构图
通过式(4)可实现坐标变换,将电压电流矢量从交流量变换为直流量,便于进行PI控制。

(4)
3.2 4QC在dq坐标系下的数学模型
利用式(4),可将电压电流矢量进行改写:
us=usdcosωt-usqsinωt
(5)
is=idcosωt-iqsinωt
(6)
uab=uabdcosωt-uabqsinωt
(7)
4QC在dq坐标系下的数学模型如式(8)所示。
(8)
3.3 评价函数的建立
对式(8)进行离散化,可得:
(9)
化简式(9),可得id(k+1)、iq(k+1)的表达式为
(10)
MPCC算法常用的评价函数为:
J(k)=[idref-id(k+1)]2+λ[iqref-iq(k+1)]2
(11)
式(11)将dq轴电流的跟踪性能作为优化目标。 为权重系数,当J(k)取得最小值时,电流跟踪效果达到最优,此时uabd(k)和uabq(k)需要满足
(12)
联立式(10)~式(12),可得uabd(k)和uabq(k)的表达式为
(13)
将最优uabd(k)和uabq(k)进行dq-αβ坐标变换,变换矩阵为
(14)
为避免运行于过调制区,需要对uabα进行约束:
uabα=sgn(uabα(k))udc
(15)
式中,sgn(uabα(k))为uabα(k)的取值符号。MPCC算法原理框图如图4所示。
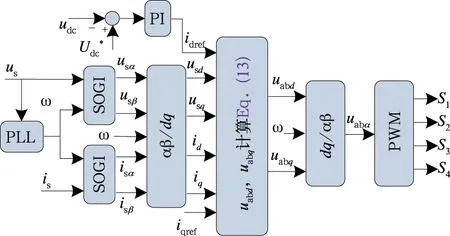
图4 MPCC算法原理框图

电气参数取值网侧电压有效值Us/V85直流侧电压给定值Udc∗/V200直流侧额定负载RL/Ω40网侧电感Ls/mH4.8直流侧支撑电容Cd/mF1.65
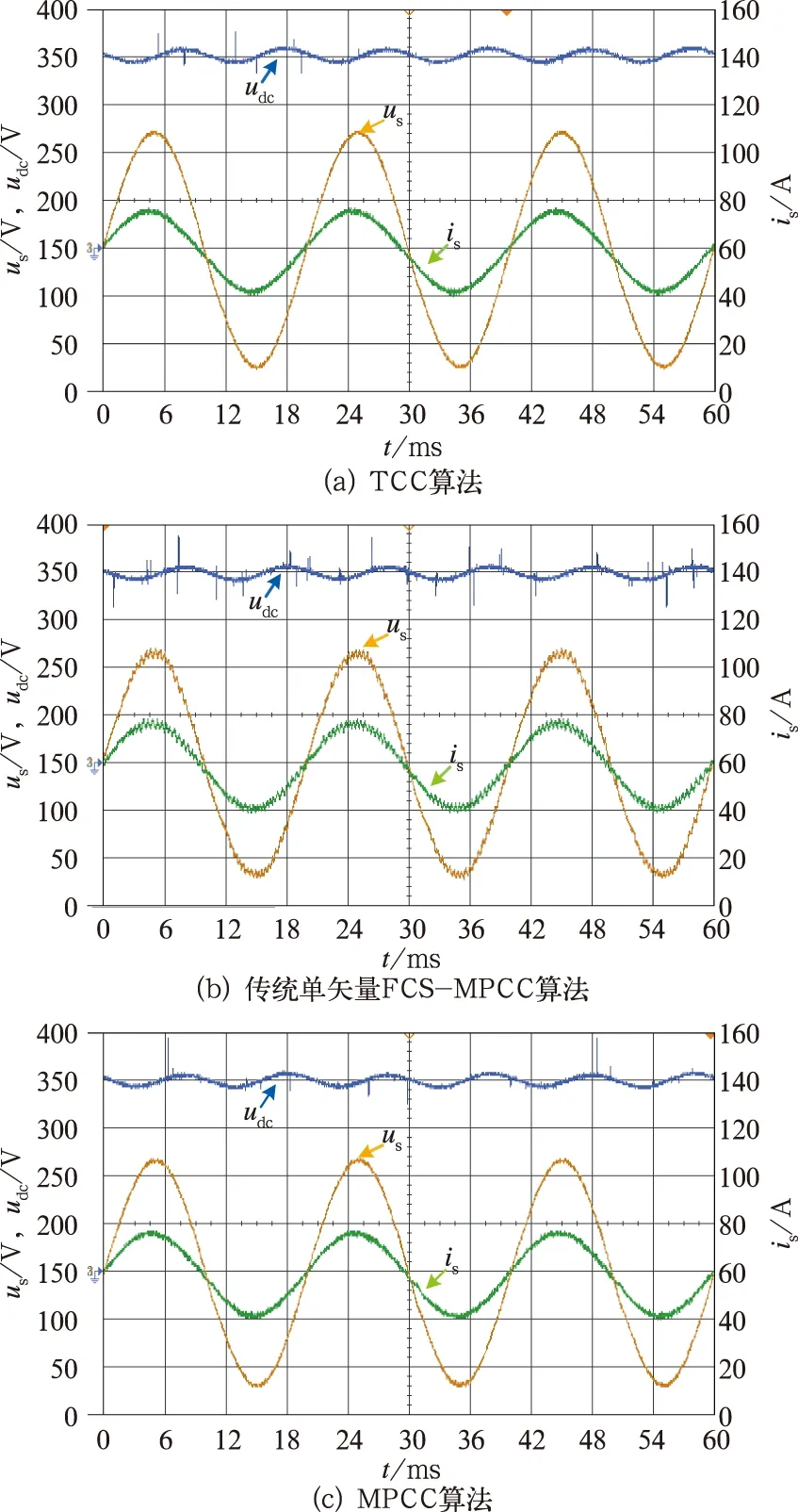
图5 稳态情况下试验波形
4 试验对比与分析
针对表1所示的电路参数,分别对TCC、FCS-MPCC和MPCC算法进行试验研究,对比3种方法的控制性能的优劣。
4.1 稳态性能对比
图5和图6分别给出了脉冲整流器稳态工作时不同控制方法的实验波形和FFT分析结果。图5(b)中,传统单矢量FCS-MPCC算法的网侧电流畸变较严重。由图 6可知,传统单矢量FCS-MPCC算法网侧电流THD为6.67%,且谐波分布广,开关频率不固定。瞬态直接电流控制算法网侧电流THD为5.12%,而该MPCC算法THD较低(4.79%)。由于采用相同的PWM调制模块,瞬态直接电流控制和MPCC算法的谐波分布在2倍开关频率附近。因此,在这3种电流控制算法中,MPCC算法稳态性能最好,同时固定了开关频率
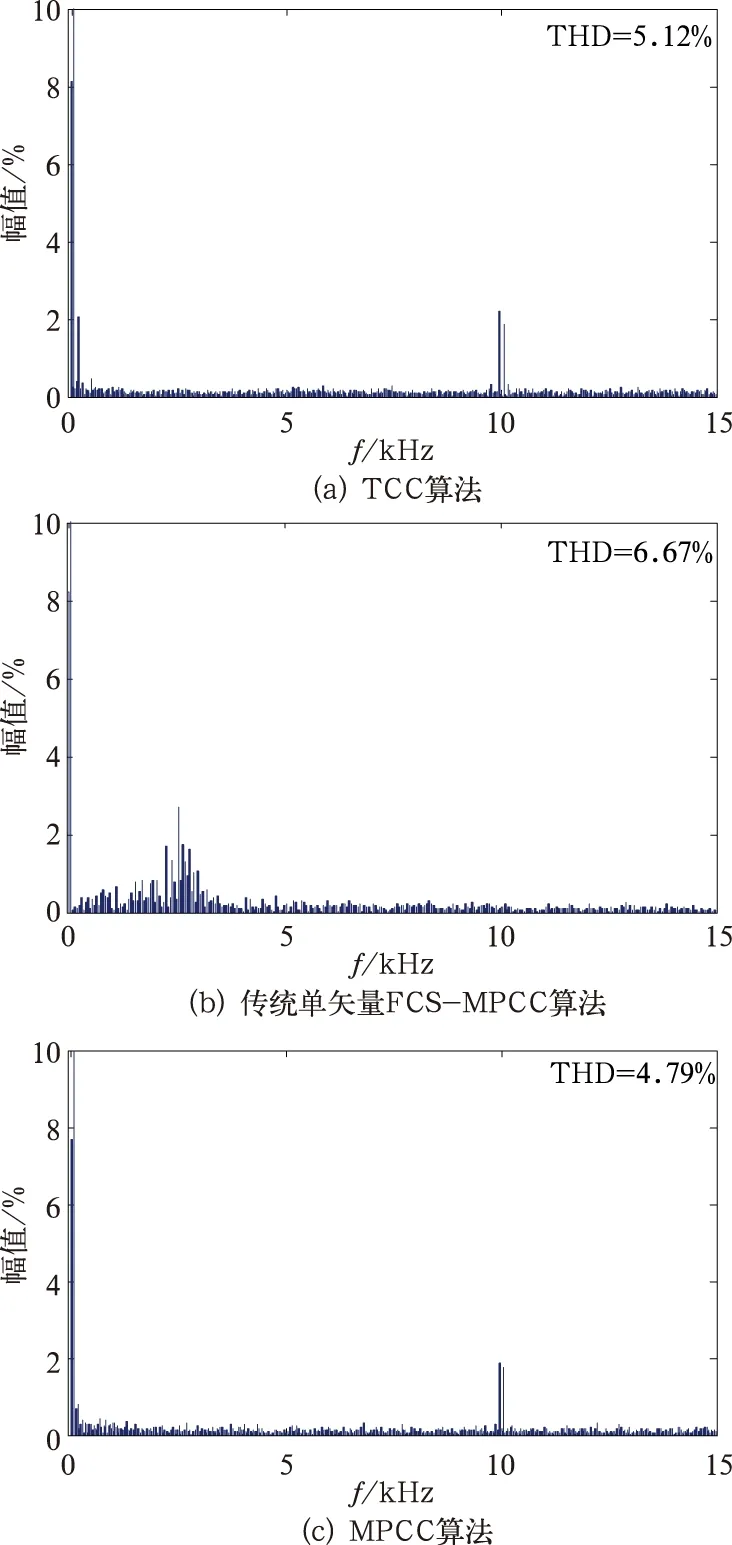
图6 网侧电流谐波分析结果
4.2 动态响应性能对比
图7给出了电流给定值idref由75%突变到100%额定电流时3种算法网侧电流is、电流给定值isref及两者电流误差ierror的实验波形。
由图7可知,传统单矢量FCS-MPCC和MPCC算法实际电流响应时间约为10 ms,优于TCC方法的响应时间30 ms,内环的动态响应速度更快。但FCS-MPCC的网侧电流误差ierror脉动明显更大,稳态控制精度低于MPCC算法。

图7 网侧电流给定突变情况下的试验波形
由图8可知,当负载发生突变时,TCC算法、传统单矢量FCS-MPCC算法和所提MPCC方法的电流响应时间约为190 ms、162 ms和155 ms,因而MPCC方法更具优势。
5 结 论
以4QC为研究对象,给出了一种MPCC电流控制算法。对TCC控制、传统单矢量FCS-MPCC和MPCC算法进行了试验对比分析,研究结果表明,MPCC算法稳态及动态电流控制均具有优势。
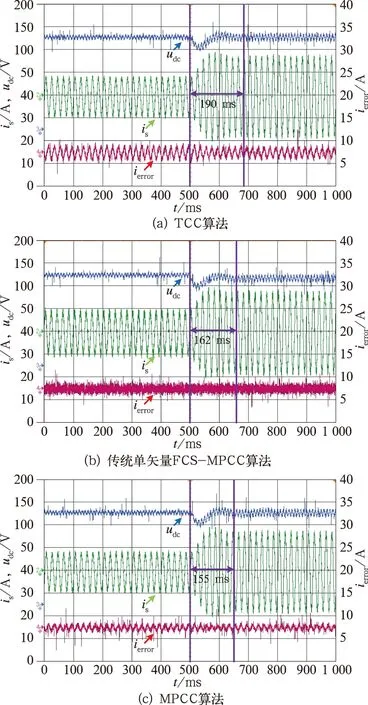
图8 负载突变情况下,直流侧电压、网侧电流及电流误差试验波形
