基于多变量选择的深度神经网络功率曲线建模
2019-09-10解加盈郭鹏
解加盈,郭鹏
(华北电力大学 控制与计算机工程学院,北京 102206)
0 引言
随着能源转型的提速,低碳化、清洁化已成为不可阻挡的趋势和潮流。其中,风能凭借其储量丰富,利用率高等特点,近年来在我国得到了快速发展。在风力发电过程中,功率曲线是表征风电输出特征的关键工具[1],也是考核机组性能的一项重要指标。对功率曲线进行精确建模对提高机组的发电效率、降低运行成本有重要作用。
风电机组生产厂家提供的功率曲线只能反映风电机组标准状态、稳定状态运行的状况,如果将其用来分析风电机组的实际运行状况就会产生明显的误差。国际电工委员会(IEC)颁布的 IEC 61400-12-1标准指出,理论功率曲线表示出了风速与输出功率在10 min内平均值的对应关系,并且采用在试验风场长时间持续测量的方法来获得[2]。而实际运行中机组的输出功率受到地形、尾流等多种因素的影响,实际发电量与预期值可能存在较大误差。因此,利用机组实际运行数据建立的实测功率曲线才是评价风电机组性能的重要指标[3]。文献[4]对风电机组功率曲线建模的目的与方法进行了较全面的综述以及批判性的分析。文献[5]提出了一种修正双曲正切的精确参数模型来表征风电机组的功率曲线。文献[6-8]提出了功率曲线的四参数逻辑函数模型、五参数模型以及九参数模型。文献[9]提出了一种基于数据分区和支持向量机算法来构建功率曲线模型的方法。但上述文献仅将风速作为功率曲线模型输入,模拟风速与输出功率的一对一映射关系,没有考虑其他对功率有影响的因素。文献[10]考虑了环境温度以及附近障碍物对风机出力的影响。文献[11]在功率曲线建模中考虑了风向因素。文献[12]提出一种Langevin模型,将功率输出拆分为确定性和随机性两部分,随机性部分考虑了风湍流等其他外部因素。但三者没有对影响风电机组输出功率的因素进行全面分析。
由于风电机组发电过程中数据采集与监视控制(SCADA)系统采集到的变量较多,这些变量与输出功率之间的关系较为复杂,其对输出功率的解释能力是未知的,且变量之间可能存在着多重相关性。文献[13]直接选取了6个变量对风电机组输出功率进行建模,而没有在数据层面分析各变量对输出功率的解释程度。本文分析了影响风电机组风能捕获和输出功率的因素,提出了采用偏最小二乘回归方法(PLS)对风电机组采集到的多种变量进行回归分析,综合考虑各个变量对输出功率的解释能力,提取出对风机输出功率影响较大的变量,同时降低了后续功率曲线建模方法的复杂度,增强模型的稳定性和适应能力;之后引入深度神经网络(DNN)进行多变量功率曲线建模。通过精度校验以及引入其他建模方法作对比,证明本文中DNN功率曲线建模的精度高,泛化能力好。
1 PLS原理
1.1 PLS算法简介
PLS是一种多变量统计分析技术,是多元线性回归、典型相关分析和主成分分析的基本功能的整合。在特征提取过程中,PLS获得的主要元素不仅可以克服自变量之间存在的多重相关性、全面地总结自变量给出的信息,而且可以很好地解释因变量,实现对高维数据的降维处理。
假设原始输入变量X∈RN×m,输出变量Y∈RN×1,其中N为样本数,m为输入变量维数。在PLS建模前需要对数据集进行归一化处理,归一化后的输入、输出分别记为X0,Y0。首先定义X0,Y0第1个主成分的轴向量ω1,c1分别是m维、n维的单位行向量。通过ω1,c1可以得到第1个主成分t1,u1,在提取主成分t1和u1的过程中需要满足以下2个条件:
(1)t1和u1尽可能多地携带X0,Y0中的信息,即:Var(t1)→max,Var(u1) →max;
(2)自变量的成分t1对因变量的成分u1有最强的解释能力,这意味着t1和u1的相关性需要最大化,即Corr(t1,u1)→max。

(1)
(2)
(3)
式中θ2为目标函数,要求取得最大值,所以ω1和c1分别为对应两矩阵最大特征值的单位特征向量。由于本文中Y0只是一个变量,所以c1是常数1,根据式(1)可得u1=Y0,根据式(2)、式(3)可得
(4)
(5)
X0与Y0对t1的回归关系为
(6)
(7)
式中:p1,r1为回归向量系数,则有
(8)
(9)
用残差矩阵X1,Y1取代X0,Y0,求第2主成分t2,并依次进行,根据交叉有效性原则确定最终的主成分个数。
1.2 交叉有效性原则

(10)

1.3 VIP指标
定义变量投影重要性指标(VIP)来表征自变量对因变量的解释能力和重要程度。自变量的VIP值越大,说明该自变量对因变量的预测越重要。
(11)
式中:Rd(Y;th)=r(y,th)为y与th的相关系数;p为主成分的个数;ωhi为轴ωh的第i个元素。
2 DNN理论基础
近年来,DNN在机器学习和人工智能领域受到了极大的关注。通过多层非线性变换,将低级特征组合在一起形成更抽象的高级特征。与单层神经网络相比,DNN表现出强大的非线性表达能力。DNN由多层自适应的非线性单元组成,每个神经层之间完全连接,通过逐层学习不断减小模型预测误差。本文所用DNN框架如图1所示,包括输入层、输出层和4个隐含层。其中输入层的神经元个数根据PLS筛选的结果确定;隐含层为全连接神经网络,每层的节点数都为70,每一层都可以表示为权重W与神经元组成的向量α相乘,再加偏差量b。

图1 DNN回归结构示意图Fig.1 Regression structure diagram of DNN
DNN回归建模的主要步骤如下:
(1)为使模型能够对高度非线性问题进行精确建模,对DNN各层增加激活函数;
αk=σ(zk)=σ(Wkαk-1+bk) ,
(12)
式中:αk为第k层的输出;Wk和bk分别为k层和k-1层之间的权重和偏差;σ为激活函数。
(2)采用Xavier初始化方法对DNN进行逐层初始化,再利用反向传播算法(BP)对DNN进行训练,这个过程中采用自适应矩阵估计(Adam)从最后一层微调各层权重Wk和偏差bk,达到各参数逐层学习不断提高DNN模型预测精度;
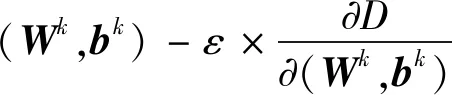
(13)
式中:ε为学习率,本文中取0.005;D为代价函数,常用均方值误差(MSE),
(14)
(3)为了防止过拟合,提高其泛化能力,采用丢弃法(Dropout)对模型进行正则化,以便提高模型泛化性能。
3 案例分析
3.1 PLS变量提取


表1 输入变量的VIPTab.1 VIP of input variables
根据PLS的交叉有效性原则与VIP指标可以得出在上述8个变量中,风速、桨距角、发电机转速、齿轮箱油温和偏航误差对风电机组输出功率的解释能力较强,故选择这5个变量作为DNN的输入变量,对风电机组功率曲线进行建模。
3.2 DNN功率曲线建模
将上述3 540条记录中的风速、桨距角、发电机转速、齿轮箱油温、偏航误差以及功率提取出来作为一个数据样本,前5个变量作为DNN模型的输入,功率作为模型的输出。具体步骤如下:
(1)由于样本中6个变量具有不同的量纲和量纲单位,为了消除变量间的量纲影响,将每个变量归一化到[0,1]区间,将前3 040个样本作为训练样本,后500个样本作为验证样本。
(2)搭建DNN模型。其中为提高模型表达能力,4层隐藏层的神经元个数都为70,选取修正线性单元(ReLU)作为激活函数,对3 040条训练样本进行训练;ReLU形式为
f(x)=max(0,x) 。
(15)
(3)回归500条验证样本。以均方根误差(RMSE)为标准对模型精度进行验证,RMSE越小,说明模型预测精度越高。

(16)
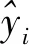
根据上述步骤可以得到验证样本的RMSE为0.045 6,验证结果如图2、图3所示(功率真实值与预测值均归一化)。

图2 DNN功率曲线建模验证结果1Fig.2 Model verification result 1 for DNN power curve

图3 DNN功率曲线建模验证结果2Fig.3 Model verification result 2 for DNN power curve
从图2与图3中可以看出,绝大多数归一化残差绝对值都小于0.1,DNN对功率曲线建模有很高的精度。在图3中,功率预测值呈带状分布,体现出风速之外的变量对输出功率的影响。
3.3 模型精度校验
3.3.1 激活函数选取校验
激活函数可以使DNN模型从简单线性空间映射到高度非线性空间,激活函数选取校验是探索DNN结构参数与输出性能之间的关系。本文计算模型建立中选取ReLU 作为激活函数,为验证其优越性,与传统的Sigmoid等激活函数进行对比。精度校验对比如图4所示,选取ReLU为激活函数时RMSE为0.045 6,而选取其余激活函数时RMSE均大于0.080 0。显然,本文中选取ReLU为激活函数预测精度高、泛化能力强。

图4 激活函数选取校验Fig.4 Selection and verification of activation function
3.3.2 隐含层节点数选取校验
在DNN中,隐含层节点数的选择也非常重要,隐含层节点数不仅对建立的神经网络模型的性能影响很大,而且是训练时出现“过拟合”的直接原因。为尽可能避免训练时出现“过拟合”现象,保证足够高的网络性能和泛化能力,本文对隐含层的节点数进行分析,结果如图5所示。当隐含层节点数为70时,该DNN模型的预测结果精度最高,其RMSE值最小。

图5 隐含层节点数选取校验Fig.5 Selection and verification of nodes number on hidden layer
3.3.3 模型精度校验
为验证本文建立的DNN功率曲线模型的准确性,引入单隐层神经网络(NN)、支持向量机(SVM)[7]和六阶多项式回归[15]来进行对比。对500组验证样本进行验证,DNN与上述3种模型对比结果如图6所示,模型校验精度见表2。
通过图6与图3对比可以看出, DNN功率曲线模型对验证集的预测结果与实际数据误差更小。同时在表2中明显可以看到DNN功率曲线建模较其他3种方法的精度有了较大的提高,对风电机组发电性能提升有较大的帮助。
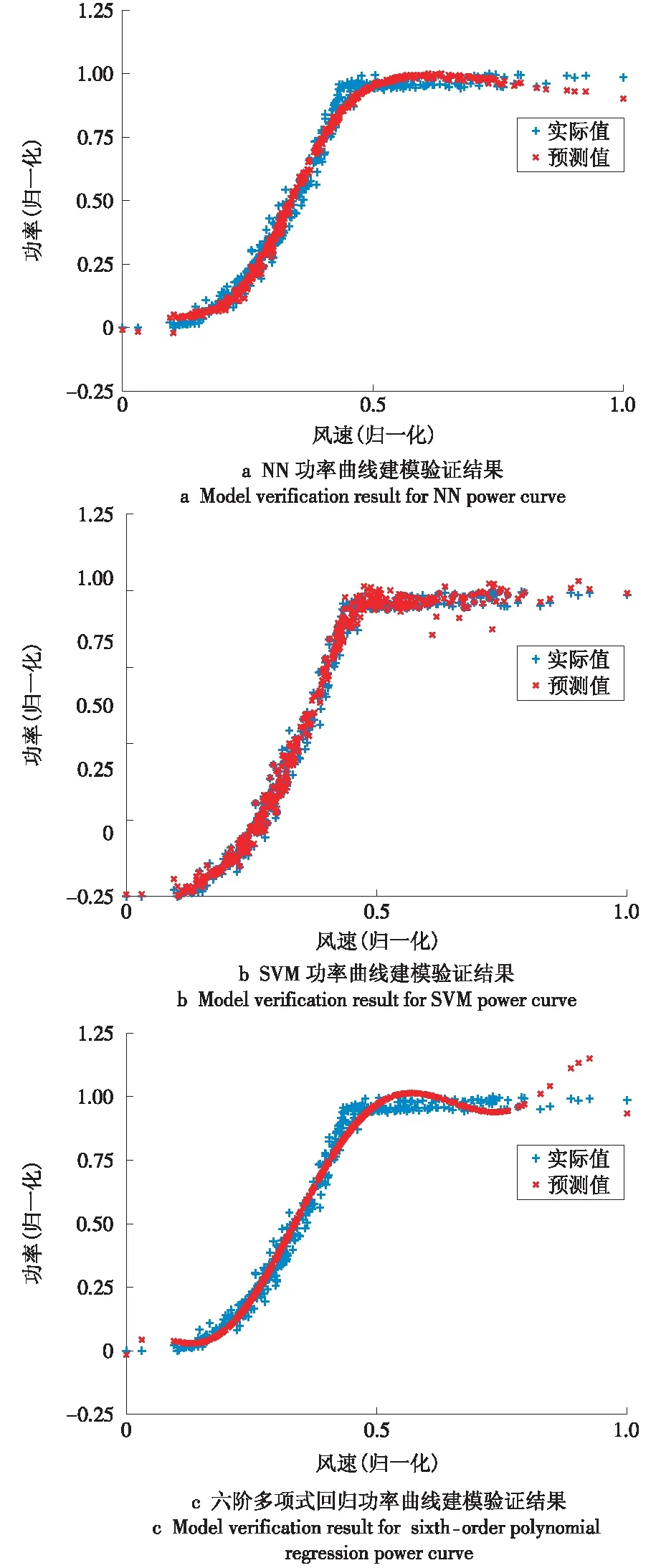
图6 NN,SVM与六阶多项式回归功率曲线建模验证结果Fig.6 Model verification result for NN,SVM and sixth-order polynomial regression power curve

建模方法RMSEDNN00456单隐层神经网络00767支持向量机00721多项式回归00941
4 结论
风电机组功率曲线能够反映机组的发电性能,利用风机历史数据对功率曲线建模更符合机组的实际运行状态。本文通过PLS对多个变量进行筛选,选用DNN对最优子集进行功率曲线建模。主要工作包括:
(1)将SCADA数据中风速、风向等20个变量作为PLS输入,功率作为PLS输出,根据交叉有效性原则和VIP指标分析输入变量与功率之间的相关程度,筛选出与对功率解释程度最强的变量子集。
(2)建立DNN功率曲线模型,通过对样本数据的训练,验证了该模型的精度。
(3)通过DNN模型激活函数及隐层节点数校验,并引入其他3种模型做对比,证明了本文采用方法的准确度。
