相干双点源干扰下的单脉冲雷达测角误差研究
2019-09-10刘恩凯何梅昕
刘恩凯,何梅昕
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)
0 引 言
单脉冲雷达[1-3]利用一个脉冲信号就能够获得目标的角度信息,具有很强的抗干扰能力。单脉冲雷达已广泛应用于现代精密跟踪雷达,尤其是末制导导引头上。这对现代重要经济和军事目标的生存构成巨大威胁,因此研究行之有效的对抗手段变得迫切。于20世纪50年代提出的相干双点源干扰(也称交叉眼干扰)[4-6],通过发射2路功率接近、相位相反的干扰信号,造成单脉冲雷达指向偏离,从而扰乱其正常工作,完成对飞机、舰船等作战平台的自卫。
相干双点源干扰是从闪烁干扰技术发展而来,一直以来,对其研究主要集中在干扰产生机理、各参数的影响以及最优布局方式等[7-16],并且这些文献大多是在通过分析2个干扰信号叠加的基础上进行的,很少有文献考虑平台自身回波带来的影响,而在舰载应用等环境下,平台的雷达反射截面积(RCS)非常大,此时必须考虑平台回波的影响。尽管文献[17]考虑了平台回波,但该文章的分析不够完备。为了深入理解相干双点源干扰及其局限性,更好地打下工程应用基础,本文在详细分析基于相干双点源干扰的单脉冲跟踪雷达接收信号模型的基础上,进行仿真分析研究。
1 单脉冲雷达测角原理
单脉冲雷达的测角原理如图1所示,其工作原理是同时产生2个波束,两波束沿天线轴线方向对称发射,且波束之间保持固定角度夹角。若波束内有目标且目标位置与等信号轴间有角偏差θ,则雷达接收端接收到的2个回波信号强度之间的差值正比于角偏差θ。通过对两接收信号进行减运算生成角量测的差值信号,通常称为“差信号”,而对两接收信号的加运算结果则是“和信号”。

图1 单脉冲雷达测角原理图
设雷达波束与等信号轴方向的夹角为θ0,目标与等信号轴方向的夹角为θ,设雷达的天线方向图为F(θ),则两雷达波束的方向图可以写为:
(1)
采用和差法获取目标的角度信息时,首先需要根据目标雷达波束接收到的目标回波信号获取和差信号:
(2)
则经过单脉冲和差网络得到的单脉冲误差信号为:
(3)
由上式可以得到误差角度信号。
2 双点源干扰原理
相干双点源干扰由2个频率完全相同,相位和幅度严格保持一定关系的干扰源组成,它一般采用如图2所示的布局方式进行自卫式式干扰。当参数选择适当时,可以使单脉冲雷达的瞄准轴超出两干扰源连线之间的方向,而产生很大的角误差。
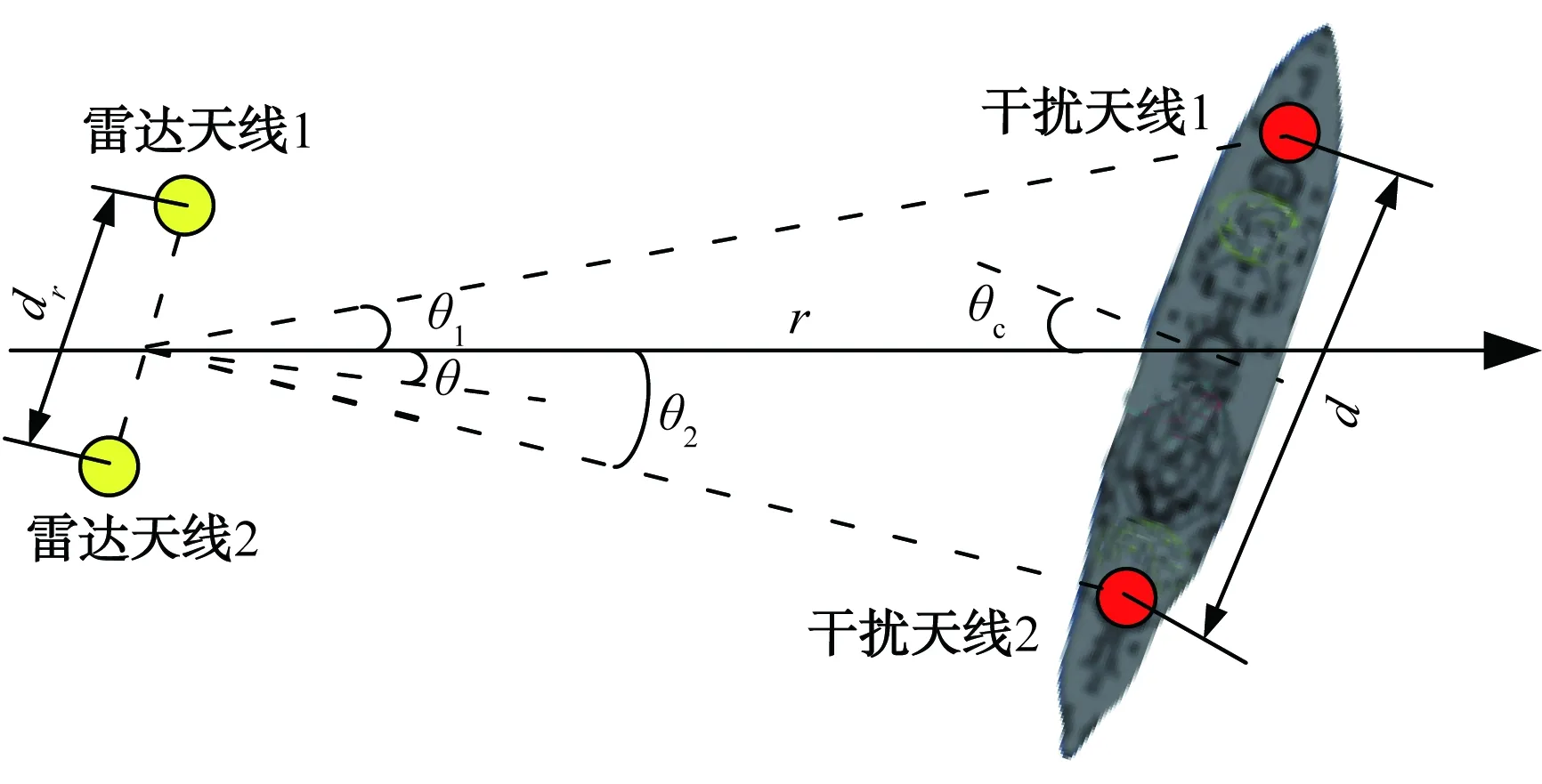
图2 相干双点源干扰布局图
相干双点源下单脉冲雷达测角示意图如图3所示,单脉冲雷达的等信号轴方向如图3所示,两干扰源与目标之间的夹角分别为θ1和θ2,雷达目标处于两干扰源的中间,与等强信号方向的夹角为θ,雷达波束主瓣与等信号轴夹角为θ0。

图3 相干双点源干扰下的单脉冲雷达测角示意图
则雷达天线1,2接收到的信号为:
(4)
式中:AJ1、AJ2和Ar分别为干扰信号1、干扰信号2和目标回波信号强度;φj为两干扰信号之间的相位差;φr为目标回波与干扰信号1之间的相位差。
则单脉冲雷达接收到的信号经过和差波束网络得到的信号为:
EΣ=E1+E2=
AJ1[F(θ0-θ1′)+F(θ0+θ1′)]ejωt+
AJ2[F(θ0+θ2′)+F(θ0-θ2′)]ej(ωt+φj)+
Ar[F(θ0-θr)+F(θ0+θr)]ej(ωt+φr)
社会治理在乡镇土地管理中的运用(李昊 ) ..................................................................................................2-31
(5)
EΔ=E1-E2=
AJ1[F(θ0-θ1′)-F(θ0+θ1′)]ejωt+
AJ2[F(θ0+θ2′)-F(θ0-θ2′)]ej(ωt+φj)+
Ar[F(θ0-θr)-F(θ0+θr)]ej(ωt+φr)
(6)
式中:EΣ为和支路信号;EΔ为差之路信号;θ1′=θ1+θ;θ2′=θ2-θ,由于目标距离r≫d,因此θ1′和θ2′非常小,临近等信号轴,则由泰勒公式展开有:
(7)
(8)
将式(7)和式(8)分别代入式(5)和式(6)有:
EΣ=2F(θ0)(AJ1+AJ2ejφj+Arejφr)ejωt
(9)
EΔ=2F′(θ0)(AJ1θ1′-AJ2θ2′ejφj+Arθejφr)ejωt
(10)
(11)
由上式可得误差角为:
(12)

由上式可以看出,误差角的大小由两干扰源间的幅度比β、目标回波与干扰信号之间的幅度比α、干扰源半张角Δθ、两干扰源之间的相位差φj以及干扰信号与目标回波信号之间的相位差φr共同决定。
3 双点源干扰下的雷达测角仿真
通过上面的数学建模和推导,建立了相干两点源干扰下的单脉冲跟踪雷达误差角的计算公式,下面对各个因素的影响进行分析。
假设两干扰源间相位差为180°,干扰源半张角Δθ为0.01°,则在干扰和雷达回波相位误差分别为10°、1°、0.1°和0.01°下,干扰误差角度与干干比、干信比的关系如图4所示。

图4 干扰误差角度与干干比、干信比的关系
由图4可以看出,干扰误差角度随着干信比、干干比和干扰/雷达回波相位误差φr的变化而变化,当干干比为1时,也即2个干扰信号功率一致时,干扰误差角度随着干信比的增大而增大,当φr=10°时,干扰误差角在干信比为20 dB时最大,为0.006°,随着φr的减小,也即干扰信号1与雷达目标回波相位逐渐接近时,干扰误差角逐渐增大,当φr=0.01°时,干扰误差角在干信比为20 dB时最大,为5°,远远大于干扰源半张角。因此,相干两点源干扰设计时,可以通过合理的选择干信比、干干比和干扰/雷达回波相位误差等参数,产生大于干扰源半张角的角度误差,致使雷达导引头跟踪在两干扰源张角之外的虚假目标。
图5为干扰/雷达回波相位误差φr=10°时,干扰源半张角分别为10°、1°、0.1°和0.01°条件下,干扰误差角度与干干比、干信比的关系。
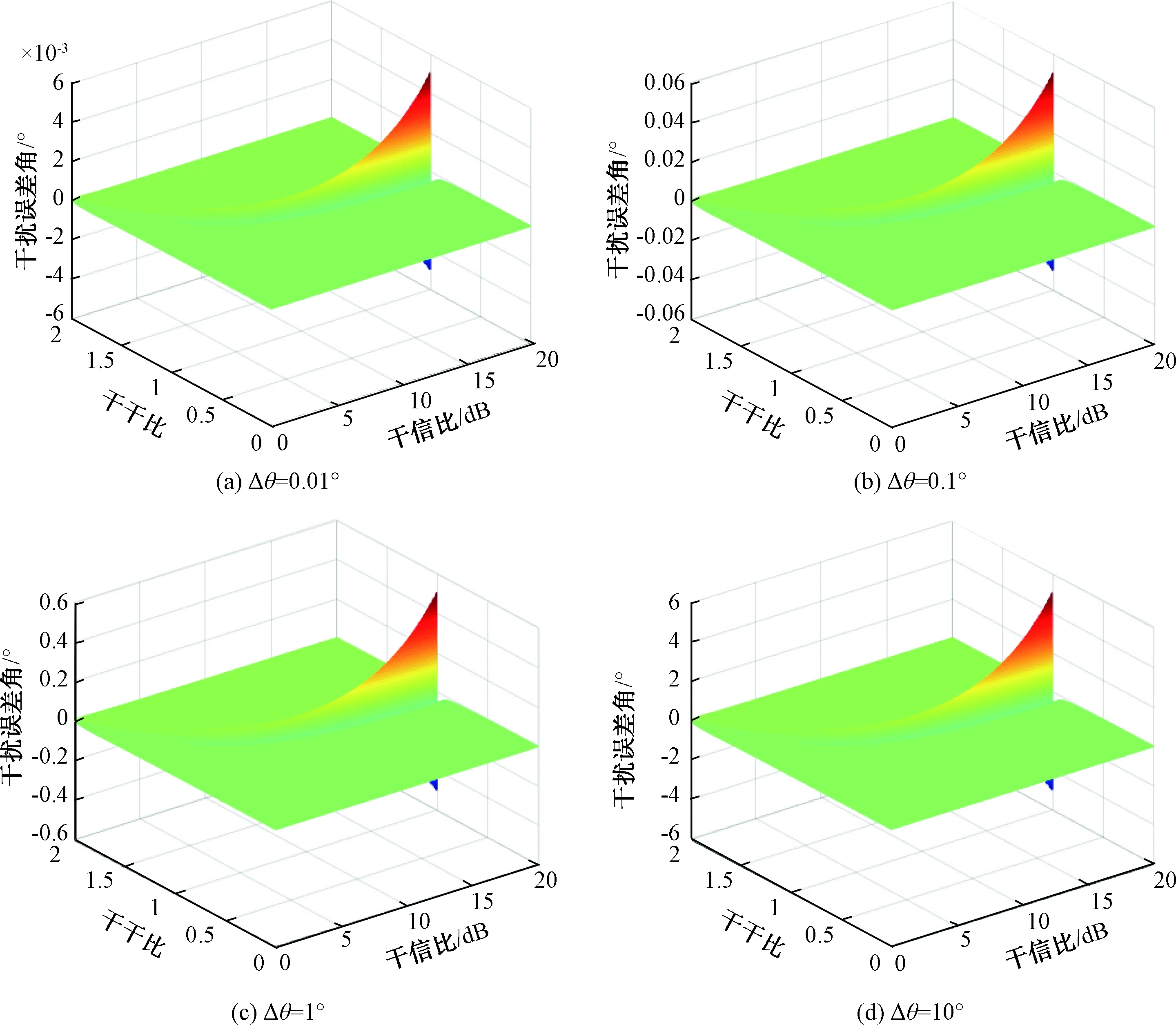
图5 干扰误差角度与干干比、干信比的关系
由图5可以看出,干扰误差角度随着干信比、干干比和干扰源半张角Δθ的变化而变化,当干干比为1时,也即2个干扰信号功率一致时,干扰误差角度随着干信比的增大而增大;当Δθ=0.01°时,干扰误差角在干信比为20 dB时最大,为0.006°;随着Δθ的增大,也即干扰与雷达之间的距离逐渐减小,干扰误差角逐渐增大;当φr=10°时,干扰误差角在干信比为20 dB时最大,为6°。因此,随着导弹与雷达之间距离的减小,干扰误差角逐渐增大。
4 结束语
本文针对相干双点源干扰下的单脉冲雷达测角误差进行研究,首先详细推导了相干双点源干扰下的单脉冲测角误差模型,并对两干扰源幅度比、目标回波与干扰信号幅度比、干扰源半张角、干扰源相位差以及干扰信号与目标回波信号之间的相位差等影响因素进行了计算机仿真。仿真结果表明,可以通过合理选择参数产生大于干扰源半张角的角度误差,致使雷达导引头跟踪在两干扰源张角之外的虚假目标。本论文的研究可以为更深入理解相干双点源干扰及其局限性打下工程应用基础。
