基于威胁评估和扩展Voronoi图的战术飞行轨迹规划方法
2019-09-10徐琳宋万强严冲张安柯
徐琳 宋万强 严冲 张安柯

摘要:针对目前各种基于Voronoi图的路径规划方法在威胁处理过程中存在的问题,提出了一种基于威胁评估和扩展Voronoi图的战术飞行轨迹规划方法。建立了基于贝叶斯网络和模糊逻辑的威胁源威胁度和路径威胁度评估模型,在此基础上建立包括路径威胁度和燃油在内的最优路径代价计算模型。结合扩展Voronoi图的路径生成方法以及Dijkstra路径规划算法,得到了从飞行起点到目标点的能够适应战场态势变化的最小代价路径。最后利用κ-Trajectory路径圆滑算法,得到了与所规划路径等长的圆滑可飞的最优路径。仿真结果验证了所提方法的可行性和有效性。
关键词:路经规划;扩展Voronoi图;威胁级别评估;路径威胁评估;贝叶斯网络;模糊逻辑
中图分类号V249.122.3 文献标识码:A
无人机或作战飞机的战术路径规划是提高复杂战场环境下作战平台生存性和完成任务有效性的关键技术之一。基于Voronoi图的无人机路径规划方法,因为其模型简洁实用和计算快速等特点,一直是目前比较常用和有效的方法[1~3]。一般在使用Voronoi图进行路径规划时,将各种威胁源放置在由n边组成的多边形内,而飞机则沿着多边形的边进行运动。通过将威胁源进行点状抽象,建立战场威胁源点阵下的Voronoi图,得到可供无人机飞行选择的初始路径集,而后对初始路径集上每段路径进行代价评估得到加权路径集,再利用对于加权图的搜索算法得到给定起始点和目标点间的飞行代价最小的路径。而在使用Delaunay图进行路径规划时,将各种威胁源连接生成三角形,而各三角形边的中点作为最佳候选航路点集,点集构成了飞行器的飞行路径[4]。
但是这种常用的基于基本Voronoi图的路径规划方法存在一些问题,首先,利用基本Voronoi图建立战场模型是一种较为定性的方式,它对不同威胁源的属性不加区分,当无人机飞过两个不同威胁源时,它选择两个威胁源连线的中点作为路径点。相比较而言,无人机如果能选择一个离高威胁源更远的点作为路径点,将可以更好地避开威胁。而基于扩展Voronoi图的无人机初始路径集生成算法[5]正体现了这一思想,它依据各威胁源的威胁度来生成路径点和路径段。
在生成了无人机的初始路径集以后,就需要对每个路径段飞行代价进行评估。沿一条路径飞行时的代价由威胁源影响下的代价和燃油消耗下的代价两方面造成。在目前路径规划算法中,计算威胁源影响下的路径代价时并不把威脅源属性考虑在内,而且也都过于定性。
本文考虑威胁源的特性,提出了一个基于贝叶斯网络和模糊逻辑的定量的威胁源威胁级别和路径威胁度度量模型,用以计算战场环境中威胁级别及扩展Voronoi图上每一个路径段在威胁源影响下的威胁度,进而得到带路径威胁度的初始路径集。并考虑到无人机的运动约束,对规划的折线路径进行平滑,同时保证实际的飞行路径与计算得到的折线路径长度相等。
1 路径规划系统结构和原理
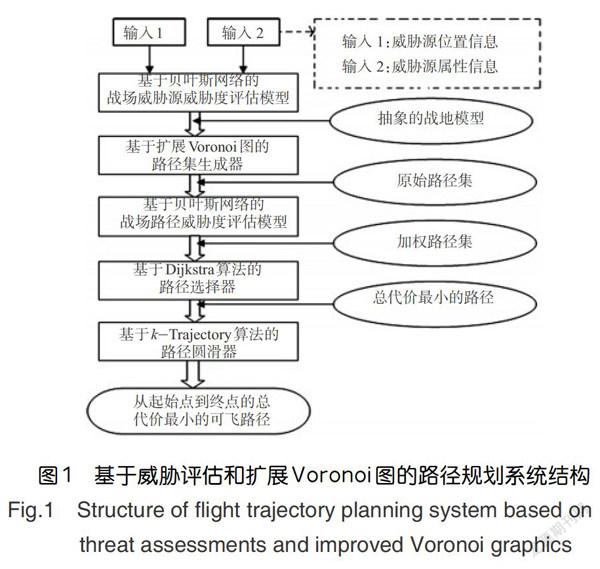
基于威胁评估和扩展Voronoi图的战术飞行路径规划系统原理和结构如图1所示。战场数据(包括威胁源的位置和属性等)被送人一个基于贝叶斯网络的威胁源威胁度评估模块,由此得到抽象的战场模型数据。而后将这些数据输入到一个基于扩展Voronoi图的路径生成模块进行处理,得到威胁躲避初始路径集,这实际上是一个有权无向图。在此图的基础上基于Dijkstra最短路径算法规划出从起始位置到目标点的威胁度最小的折线路径。最后根据平台性能约束要求,基于κ-Trajectory算法的路径圆滑器对折线路径进行平滑处理,得到一条飞机实际可飞的最短路径。
因为在这个框架中考虑到了威胁差异,所以它可以更好地适应战场环境和态势的动态变化。
2 威胁源威胁度评估模型
考虑到战场环境的不确定性、随机性、定性和定量并存,而贝叶斯网络(Bayesian Networks,BN)和模糊逻辑具有与人类相似和透明的诊断和推理过程,能较好地处理不确定性和不精确信息,非常适合态势评估这种不确定性环境。基于贝叶斯网络的态势评估原理如图2所示[6]。
但贝叶斯网络对于连续输入情况不太方便,而模糊逻辑可方便地将连续的输入模糊离散化,并作为贝叶斯网络的输入。另外,由于贝叶斯网络输出为一个概率矢量,不便直观的决策和应用。为此,可进一步通过模糊逻辑推理得到一个0~1之间的标量值,原理如图3所示[7]。
2.1 贝叶斯网络推理过程
图4为一个典型的树状贝叶斯网络,假设节点X有m个子节点Y1,Y2,…,Ym和一个父节点U,定义符号:Bel为节点的信度值或后验概率分布,λ为从子节点获得的诊断信息,π为从父节点获得的因果信息。
贝叶斯网络推理规则由条件概率矩阵确定:
MX|U=P(X=x|U=u)
表示父节点U中某态势u发生情况下子节点X中某事件x发生的概率。算法以单个节点为中心,从子节点得到λ,从父节点得到π,计算本节点的Bel、λ和π,并触发相邻节点进行更新,其更新过程为[8]:
(1)更新自身的置信度
Bel(x)=αλ(x)π(x)
π(x)=πX(u)MX|U式中:α为规一化算子。
(2)自底向上更新
λx(u)=λ(x)MX|U
(3)自顶向下更新
贝叶斯网络更新由事件触发,是基于诊断的推理过程。
2.2 威胁源等级评估
无人机战术任务及飞行路径规划的重要影响因素就包括对威胁源等级高效准确的评估。而战场中常见的威胁源主要有敌方雷达、地防导弹、高射炮等,可以采用贝叶斯网络和模糊逻辑对各种威胁源对平台的威胁级别进行评估[9],原理如图5所示。
本文将贝叶斯网络中各节点的状态信息集合定义为:
威胁源的类型:Id={雷达,导弹,高炮}
威胁源级别:Threatlevel={高,中,低}
飞机对抗威胁源的能力:Ability={好,中,差}
飞机与威胁源有效威胁区域(如杀伤范围)的相对位置和方位关系:Wez={内,边,外,方位}
其中飞机对抗威胁源的能力Ability以及与威胁源有效威胁区域(如杀伤范围)的相对位置和方位关系Wez由模糊推理系统推理得到。
贝叶斯网络输出的根节点的后验概率(或信度值)即为根据各节点信息集得到的威胁源威胁级别评估结果:
Bel(Threatlevel)=P(Threatlevel={高,中,低})
本文中网络的输入包括两部分:初始化输入和实时信息输入。而初始化输入也包括两部分预先确定的信息:网络节点的条件概率矩阵以及根结点的先验概率。其中先验概率记为:
π(Threatlevel)=P(Threat={高,中,低})
在模拟过程中输入的子结点信息被定义为实时信息输入,实时信息输入记为:
λ(Ability)=P(Ability={好,中,差})
λ(ld)=P(Id={雷达,导弹,高炮})
λ(Wez)=P(Wez={内,边,外,方位}
在先验信息为零的情况下,假设各种状态为等概率时间。假设先验概率π(Threat)=(0.3,0.4,0.3),网络的其余输入分别初始化为λ(Ability)=α(1,1,1),λ(Id)=α(1,1,1),λ(Wez)=α(1,1,1,1)。见表1推理规则条件概率矩阵,威胁等级评估规则由先验概率矩阵MId|Theratlevel,MAbility|Threatlevel和MWez|Threatlevel给出。当网络初始化信息输入完毕后,网络进入等待状态。当有新的实时信息输入时,贝叶斯网络推理启动仿真流程。
表2为三种不同威胁源的仿真结果。以第一组数据为例,由于我方对抗威胁源的能力较强,且处于威胁源攻击范围之外,敌方威胁源有较高可能为高炮,杀伤力较弱。贝叶斯网络的评估结果为:威胁程度为高、中、低的概率分別为0,0.047,0.953,结果符合常理。
上面得到的Threatlevel是一个矢量,为此在威胁级别评估基础上,采用模糊推理方法确定各威胁源的加权因子,即通过模糊推理得到各个Threatlevel对应的一个唯一的威胁度。
2.3 威胁源相对威胁度的单值化模糊推理
单值化模糊推理是指在同时存在多个威胁源的战场,根据威胁级别对威胁源进行威胁排序,并将各威胁源的威胁度或优先级表示为归一化模糊权值qi[10]:i=雷达,导弹,高炮
基于战场有多个威胁源,在得出各威胁源威胁度的基础上,采用模糊推理方法推理得出各威胁源的相对重要性权值。规则的一般形式为:当Threatlevel为高时,q为高;当Threatlevel为中时,q为中;当Threatlevel为低时,q为低。
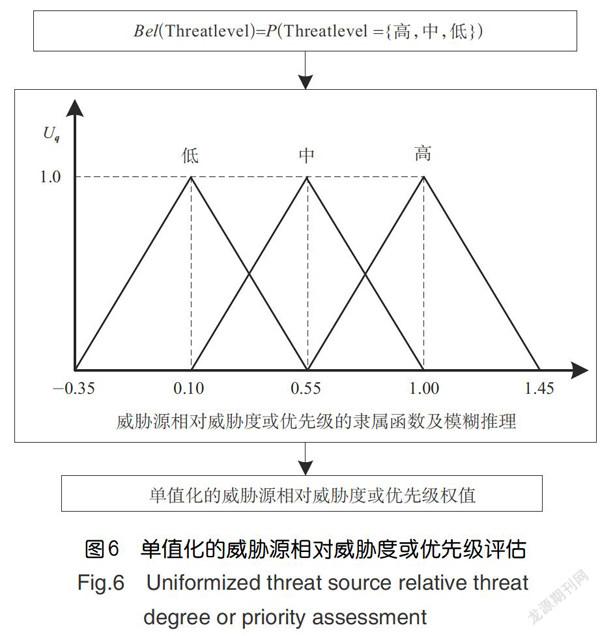
相应威胁级别的后验概率P(Threadevel=[高,中,低”。图6为规则结论部分采用三角形隶属函数。为给不重要的威胁分配一个较小的权值,图中权值的范围为[0,1]。
威胁源相对重要性权值的模糊推理方法流程如下:用每条规则条件部分的信度值Bel(Threadevel)对规则中各个模糊变量的成员函数分别进行裁剪。将裁剪以后的同一加权因子的成员函数叠加起来,求出叠加所形成的阴影部分的质心位置qiC和面积Ai(i=1,2,…),采用质心解模糊方法得到表征每个威胁源重要性程度的模糊权值:
qiS=qiC×Ai,i=1,2,…
规范化处理得到多威胁源相对重要性程度的归一化权值:
假设战场中有4个威胁源,其威胁级别评估结果分别为Bel1=[0,5,2,3],Bel2[0,2,3,5],Bel3=[0,4,6],Bel4=[0,6,2]。以第一个威胁源为例,则有P(Threatlevel,={高,中,低})=[0,5,2,3]。图7为根据权值的模糊推理过程,得到模糊权值q1的成员函数被Bel1裁减叠加以后形成的图形。采用质心解模糊方法得到这4个威胁源的模糊权值分别为 q1S=0.44955,q2S=0.321975,q3S=0.1962,q4S=0.4833。经过规范化处理,得到规一化的相对模糊权值q1=0.309815,q2=0.221895,q3=0.135215,q4=0.333075。作为决策规划的主要依据,规一化的相对模糊权值的大小综合反映了威胁源的威胁度以及相对重要性程度。
2.4 威胁级别的动态评估实例
假设战场中有4个威胁源:两个雷达、一个导弹和一个高炮,各威胁源的威胁范围由圆圈来表示,具体分布如图8所示。而飞机由坐标(0,0)至(300,300)沿直线飞行。
图9为由贝叶斯网络和模糊推理得到各威胁源对飞机威胁程度的连续动态评估结果。从图9可以看出,各威胁源的相对威胁程度是随飞机位置动态变化的,这反映了战场态势的变化过程。
图中表征各威胁源相对重要性程度的权值采用了归一化处理,从图中可以看出雷达对飞机的威胁程度相对导弹和高炮而言,要小得多。这是由表1给出的条件概率矩阵事先假定雷达威胁程度较低造成的。
3 基于扩展Voronoi图的路径生成模型
3.1 扩展Voronoi图的基本思想
扩展Voronoi的基本思想及生成原理(如图10所示)为:
(1)规则1:距离与威胁成比例原则
如图10(a)所示,当无人机从两个威胁度不同的威胁源之间穿过时,无人机不再像简单Voronoi图的路径选择方法那样只是选择两个威胁源的中点,相反,它会先考虑两个威胁源各自的威胁值,然后会选择一个更加远离高威胁度威胁源的点经过,而这个点的选取规则直接跟威胁源的威胁度成反比关系。
(2)规则2:扩展Voronoi图的生成原则
考虑三个威胁源的情况,如图10(b)所示,威胁源W1,W2,W3组成一个三角形,我们可以在三角形AWlW2W3的三条边上根据规则1分别确定三个点,即线段Wl W2上的点A、线段W1W3上的点B和线段W2W3上的点C。与此同时,为了能够找到连接这三个点的合理路径,将AABC的内心点D也作为路径点选择出来,这样在ΔW1W2W3内的可行路径就是AD,BD和CD。
3.2 基于扩展Voronoi图的路径生成
考虑一个有很多威胁源的战场,为了建立这样一个战场上无人机可飞的初始路径集,先根据战场威胁源的位置,对战场进行Delaunay三角分割[11],把战场分割成很多个三解形区域。对Delaunay分割后的每一个三角形区域,在计算三角形顶点对应的三个威胁源的威胁度之后,利用上述计算原则得到三角形中4个合适的飞行点,由此可以得到相应三角形内合适的初始路径。最后,把各个三角形内的可行初始路径相连接,即可得到整个战场下的基于扩展Voronoi图的初始路径集。
4 路径威胁度评估模型
4.1 路径威胁度评估原理
为了找到扩展Voronoi图的每一条边的总的路径代价值,首先考虑路径段上一个采样点在一个威胁源影响下的威胁度,如图11所示。整个路径由路径段构成,而每个路径段则由若干采样点构成。
整个路径威胁由路径段威胁总和构成,而路径段的威胁则由该路径段上采用点的威胁总和构成,每个威胁源对采样点的威胁度评估采用前述的基于贝叶斯网络和模糊逻辑方法实现。
4.2 路径段受所有威胁源影响时的威胁代价
为计算一条路径段上的总威胁度,需要先在该路径段上取一定数目的采样点,本文取L;/6,L;/2和5L,/6路径点进行计算,其中Li是路径i的总长度。求各采样点受所有威胁源影响的总威胁之后,取所有采样点威胁度的平均值作为当前路径段上各点威胁度的参照量,然后将此参照量与路径段长度相乘得到该段路径的总威胁代价(如图11所示)。
路径段威胁度度量的计算公式如下:式中:S为路径段上所取的采样点的总数目;T为战场威胁源总数目;i为战场威胁源的索引;j為路径上的采样点索引;kji为第i个威胁源对采样点j的威胁度;L为当前路径段总长度。
4.3 考虑威胁和燃油时路径段总代价
虽然燃油代价的计算方法各有不同,但是考虑到燃油代价必然与当前路径段长度成比例,同时考虑到路径上单点的威胁度度量范围在区间[0,1]内随机分布,于是路径长度为L的路径的威胁度为[0,L]内随机分布,取其平均值作为燃油代价:
Kfuel=μ×L=0.5×L式中:μ为燃油消耗速率因子,本文中取0.5。
路径段的总代价公式可以表示为:
J=k×Kthreat+(1-k)×Kfuel,0≤k≤1式中:k为加权因子,表示威胁和燃油之间的相对权重或偏好,k取值较大,表明应该多考虑路径威胁度的影响,而k取值较小则表明更关注燃油消耗的影响。
5 路径规划与平滑算法
在求得无人机的所有代价初始路径集之后,采用Dijkstra算法[12]规划出从起始点到目标点的最短折线路径,然后需要对这条路径进行平滑处理,以得到一条无人机实际可飞的路径。
考虑到无人机的最小转弯半径限制,记这个量为R,此处采用κ-Trajectory算法[13],利用一些半径大于R的圆来实现路径平滑的目标,如图12所示。考虑初始折线路径P1P2P3,如果无人机在线段P1P2上一个合适的位置A开始转弯,沿着图10等半径圆上弧线AO1A1,A1OB1和B1O2B飞行,那么适当选择飞行半径,就可以使得弧行路径的总长与折线路径的总长相等。
事实上,令图12中圆O和圆Ot的圆心位置满足:
则路径的实际距离与理论距离的差值为[11]:
其中:
通过分析可以得到:
上述结论对任意的β都适用,所以必然有一个满足条件的κ,使得∧(κ)=0,利用牛顿二分法可以得到想要的K值,并且可以通过控制迭代步数得到想要的精度,也就是可以确定一条与折线路径等长的圆滑的飞行路径。
6 仿真结果与分析
设战场威胁分布如图13(a)所示,用圆圈代表威胁源,用星形代表无人机的起始和目标位置,如图中P1和P10所示。为了能够找出一条从起始点到目标点的总威胁代价最小的路径,需要先给出威胁源的位置以及属性信息作为输人,而后采用基于贝叶斯网络的威胁源威胁度评估算法和基于模糊算法的威胁度单值化算法得到抽象的战场模型,即战场各威胁源威胁级别评估结果,见表3。在此基侧上得到扩展Voronoi图及无人机初始飞行路径集,而后利用基于贝叶斯网络的路径威胁度算法求得初始路径集上每一路径段的总的威胁代价,得到具有总威胁代价的加权路径集,这实际上是一个无向加权图,此时利用经典的Dijkstra算法可以规划一条从起始点到目标点的最短折线路径,最后结合飞机的飞行条件限制,可以用K-Trajectory算法将最短折线路径平滑为一条飞机可飞的路径。
在图13(a)中,实线是基于扩展Voronoi图(IVG)算法得到的无人机初始路径集,而虚线则是利用基本Voronoi图BVG算法得到的初始路径集。从图中可以清楚地看到,IVG图的各边明显要远离威胁度高的威胁源,更好适应了战场态势情况,而BVG图却对于威胁源的高低不加区别。
考虑威胁源和燃油影响下的路径代价,基于IVG算法得到的初始路径集以及不同Voronoi图规划出的最短路径如图13(b)所示。可以清楚地看出:基本Voronoi图BVG算法得到的路径并没有远离威胁源集中区域和高威胁源;基于扩展Voronoi图IVG算法,利用经典的Dijkstra算法,依据战场态势和威胁评估结果,得到一条从起始点尸1到目标点P10的拆线路径{P1,P2,…,P10},此路径远离了威胁级别较高和威胁源相对比较集中的区域,规划结果更为合理。
最后利用K-Trajectory路径圆滑算法,得到了与所规划路径等长的圆滑的可飞路径,如图13(c)所示。
仿真结果表明,本文提出的基于威胁评估和扩展Voronoi图路径规划算法更好适应了战场态势,因为该方法综合考虑了威胁源的不同属性和威胁级别的相对大小,可以更好地适应战场态势的变化。
7 结论
本文提出了一个基于威胁评估和扩展Voronoi图的战术飞行路径规划方法。建立了基于贝叶斯网络和模糊逻辑的威胁源威胁度评估模型和路径威胁度模型,在此基础上建立了一个新的路径威胁度的计算模型,通过两个威胁度评估模型和基于扩展Voronoi图的路径规划方法的结合,得到了从起点到指定目标点的总路径代价最小的路径,并且该路径远离了威胁级别较高和威胁源相对比较集中的区域,可以更好适应战场态势的动态变化。考虑到飞行平台的性能约束,利用K-Trajectory路径圆滑算法,得到了与所规划路径等长的圆滑的可飞路径。仿真结果进一步证实了所提方法的可行性和有效性。
参考文献
[1]McLain T W,Beard R W Trajectory planning for coordinatedrendezvous of unmanned air vehicles[J].Fire Control&Command Control,2009,34(2):1247-1254.
[2]Beard R W,McLain T W,Goodrich M A,et al.Coordinatedtarget assignment and intercept for unmanned air vehicles[J].IEEE Transaction on Robotics and Automation,2002,18(6):911-922.
[3]McLain T W,Beard R W.Coordination variables,coordinationfunctions and cooperative timing missions[J].Journal ofGuidance,Control and Dynamics,2005,28(5):150-161.
[4]Zhu R,Sun D,Zhou Z.Cooperation strategy of unmanned airvehicles for multitarget interception[J].Journal of Guidance,Control and Dynamics,2005,28(5):1068-1072.
[5]肖秦琨,高曉光.一种无人机局部路径重规划算法研究[J].飞行力学,2006,24(1):86-89.
[6]Mulgund S S,Zacharias G L.A situation-driven adaptive pilot/vehicle interface[C]//Human Interaction with ComplexSystems Symposium,1996.
[7]董卓宁.无人机突情感知与突情处理智能自主控制技术研究[D].北京:北京航空航天大学,2010.
[8]Pear J.Probabilistic reasoning in intelligent systems:Networks of plausible inference[M]San Francisco,CA:MorganKaufmann Publishers,INC,1998.
[9]Hanson M,Sullivan O,Harper K.On-line situation assessmentfor unmanned vehicles[C]//Proceedings of the ArtificialIntelligence and Research Society(FLAIRS)Conference,FLorida,2001.
[10]周锐,余舟毅,池沛,等.战术辅助决策系统中的态势评估问题研究[J].系统仿真学报,2005,17(9):2130-2133.
[11]周培德,卢开澄.计算几何:算法分析与设计[M].北京:清华大学出版社,2005.
[12]卢开澄.图论及其应用[M].北京:清华大学出版社,1995.
[13]Anderson E P,Beard R W,McLain T W.Dynamic trajectorysmoothing for UAVs[J].IEEE Transactions on Control SystemTechnology,2003(5):3-13.
