四边形特性阻抗继电器测试分析

彭洋

摘 要：距离保护在电力系统中使用较为广泛，常常用于高压输电线路以保障其运行的稳定性。但是，由于故障时过渡电阻的存在，将直接影响距离保护动作的正确性，造成保护误动、拒动或者灵敏度降低等问题。目前，国内外提出了多种消除过渡电阻对距离保护的影响的解决方案。虽然提出的解决方案众多，但由于电力系统运行的复杂性，许多方案仍然处于试验阶段。基于此，本文首先阐述了过渡电阻在单侧电源线路和双侧电源线路中发生短路故障时会出现的问题，然后以四边形特性阻抗继电器为例，分析不同特性阻抗继电器在经过渡阻抗影响时的工作原理，并对四边形特性进行测试动作边界的实验分析。实验结果表明，阻抗角的选择精确度越高，与四边形特性的阻抗继电器的理想图形越近似，边界倾角偏差越小，能极大地提高系统运行的稳定性。

关键词：距离保护;过渡阻抗;四边形阻抗继电器

中图分类号：TM58 文献标识码：A 文章编号：1003-5168（2019）01-0116-06

Test and Analysis of Quadrilateral Characteristic Impedance Relay

PENG Yang

（Southeast University Chengxian College，Nanjing Jiangsu 210088）

Abstract： Distance protection is widely used in power system， often used in high voltage transmission lines to ensure its stability. However， due to the existence of transition resistance in fault， it will directly affect the correctness of distance protection operation， resulting in protection maloperation， rejection or sensitivity reduction. At present， many solutions to eliminate the influence of transition resistance on distance protection have been proposed at home and abroad. Although there are many solutions proposed， many of them are still in the experimental stage due to the complexity of power system operation. Based on this， this paper first expounded the problems of short-circuit fault of transition resistance in unilateral power supply line and bilateral power supply line. Then， taking quadrilateral characteristic impedance relay as an example， it analysed the working principle of different characteristic impedance relay when it was affected by transition impedance， and carried out experimental analysis of quadrilateral characteristic test action boundary. The experimental results showed that the higher the accuracy of impedance angle selection was， the closer the impedance relay with quadrilateral characteristics was， and the smaller the deviation of boundary inclination angle was， which could greatly improve the stability of system operation.

Keywords： distance protection;transition impedance;quadrilateral impedance relay

1 研究背景

目前，中国电力行业迅猛发展，电力系统的规模变得日益庞大，使用的电压等级越来越高，电网结构也变得越发复杂。目前，高压输电线路在电网中使用较为广泛，而保证高压输电线路的运行稳定性，就成为当前电网亟待解決的问题。在电网运行复杂的情况下，距离保护能为高压输电线路提供保护。距离保护是利用电压、电流比值关系来判断故障的一种保护，灵敏性高，能在较短的时间范围内将检测到的故障切除，且不受系统运行方式影响[1]。但是，距离保护仍存在一定的弊端，如一旦线路中出现测量到的阻抗值等于或小于整定阻抗值，将会使电压突然消失，保护误动作。因此，为了保证距离保护在高压输电线路中的可靠性，要采取相应的防范措施。

距离保护中出现的测量阻抗值小于整定阻抗值的情况，通常是由于系统发生故障时，短路点存在过渡电阻造成的。过渡电阻是系统发生故障时，两相间或者相与地间存在的电阻。当电力系统中存在故障时，由于过渡电阻的存在，系统中的电流、电压关系将发生变化，严重情况下还会导致保护装置无法工作。在接地故障时，过渡电阻值通常可达到数百欧姆，对系统的损害程度较大。这些都会对继电保护的设计、运行、调试、整定计算造成影响。由此，本文针对过渡电阻的特性，重点分析其对三段式距离保护的影响。

2 国内外研究现状

为了消除过渡电阻的影响，国内外进行了一系列实验研究。例如：华北电力大学实验室黄少峰[2]等人基于全周傅氏算法提出了用保护处负序电流相位近似代替故障点处故障电流相位的方法，并通过传统阻抗测量方法的改进，在高阻接地的情况下也能够比较准确地求得测量电抗值。EMTDC仿真表明，与传统的计算方法相比，该算法能有效减小过渡电阻对测量阻抗的影响，保证测量阻抗的准确性。此外，黄少峰教授还提出了介绍了一种不受系统振荡影响的多相补偿阻抗元件，利用序分量法分析了线路单相经过渡电阻短路时该多相补偿阻抗元件的动作特性，分别从保护区内、区外以及反向故障3个方面分析了过渡电阻对该多相补偿阻抗元件的影响[3]。浙江大学何奔腾教授通过对阻抗变化轨迹公式的推导和分析，提出了一种基于阻抗轨迹估计的自适应四边形距离继电器的原理及实施方案。该继电器利用故障前系统正常运行时电压和电流的测量值，实时估计出阻抗变化轨迹，并自动调整继电器的动作特性。理论分析和仿真计算表明，提出的自适应距离继电器可应用于相间距离保护，可有效防止区外经过渡电阻故障时发生超越，同时在区内故障时提高耐受过渡电阻能力[4]。连晶晶[5]等在《四边形特性阻抗继电器探讨》一文中通过对四边形特性阻抗继电器在克服短路点过渡电阻的影响和躲过负荷阻抗等方面优良特性的分析，研究了四边形特性阻抗继电器的实现方法和特性。南瑞继保公司的PCS-931G系列线路保护中，快速距离保护采用工频变化量距离继电器，而三段式距离保护采用电压极化距离继电器，国电南自的PSL-603U系列线路保护中，快速距离保护采用工频变化量距离继电器，三段式距离保护采用阻抗继电器[6]。早在1999年《中国电机学报》中，段玉倩、贺家李教授就提出了基于人工神经网络的距离保护原理，利用神经网络可操作性、适应性强的特点，搭建出新型网络模型[7]。后期研究时，将实际线路发生故障时的数据代入网络模型中进行训练，解决自适应距离保护中存在的多种问题。包括使用各种滤波手段，采取整定零序电抗线或者DPFC算法分析线路中故障发生的位置，对距离保护中的边界范围进行准确判断，这样不仅提高了保护装置的灵敏性，而且有利于快速切除故障，提升系统的性能。

3 问题提出

过渡电阻在系统中的影响具有复杂性，无论是采用改变阻抗偏移角，还是利用各电量的相量关系、搭建网络模型，都需要根据实际电力系统情况确定最准确的实验方案，把影响范围降至最低。本文以单、双侧电源线路为例，分析过渡电阻如何直接影响距离保护动作的正确性，并造成保护误动、拒动或者灵敏度降低等问题。在探究四边形特性阻抗继电器元件的同时，确定四边形的边界条件和角度范围。根据距离保护的三段式特性和四边形元件的边界情况，运用了两种测试方案，用于获取精确的测量阻抗值。

4 过渡电阻的影响

4.1 单侧电源线路经过渡电阻短路

图1为单侧电源线路经过渡电阻短路时的等效图，图2为过渡电阻对不同安装地点距离保护的影响，当线路BC的始端经过渡阻抗在K点发生接地故障时，保护1处的阻抗值为短路所得的测量阻抗值[Rt]：

[Zk.1=Rt]                               （1）

保护2处测得的阻抗值为AB段实际线路阻抗与经K点发生短路故障时过渡阻抗[Zk.1=Rt]的相量叠加和[8]：

[Zk.1=Rt+ZAB]                         （2）

<C：＼Users＼hnkj＼Desktop＼河南科技（创新驱动）2019年第01期_103595＼Image＼Y@AT～～@3TKH（KT[F[%`F8VT.png>[M][A][2][B][1][k][C][Rt]

图1 单侧电源线路经过渡电阻短路的等效图

<F：＼欢欢文件夹＼201904＼河南科技201901＼河南科技（创新驱动）2019年第01期_103595＼Image＼UAJ6PV48@AYQT}TGJ00{PWK.png>[A][R][R][Zk，2][Rt=Zk，1][B][C][jX][jX]

图2 过渡电阻对不同安装地点距离保护影响分析

假定在线路BC的始端发生接地故障，以A侧装置的距离继电器为例，装置A可用于保护线路AB的80%左右（一般为80%～85%）。图中以A为坐标原点的小圆，作为A的Ⅰ段保护方向圆。B侧的Ⅰ段可以用于保护线路BC的80%左右，B的Ⅰ段保护在图中为以B为坐标原点的圆。图中A侧的Ⅱ段保护，保护至B的Ⅰ段范围内。其中，在AB段的阻抗值上叠加电阻分量[Rt]，叠加后的阻抗[Zk.2]值落在B段保护边界上，也处于A的Ⅱ段阻抗圓动作区内。随过渡电阻[Rt]增大，A的保护2超过范围动作，B保护拒动[8]。由分析可得，过渡电阻的存在，将直接影响保护的准确度，随着线路不断增加和故障区域范围增大，保护会发生拒动。只有不断增加装置的保护范围，才能避免超范围或者拒动的问题。该做法耗损较大，且扩大装置的保护范围的难度较高，所以该方案暂不采用。

4.2 双侧电源线路经过渡电阻短路的分析

与单侧电源线路相比，双侧电源线路存在送电端和受电端的区分，由于选取的位置不同，所测的阻抗值、使用公式也不同。接下来分析双电源线路的工作原理。图3为双侧电源线路经过渡电阻短路的等效图;图4为过渡电阻对不同安装地点距离保护的影响。

如图3所示，在双侧电源线路中，有两端的电流通过接地电阻注入故障点，A所在的一端电流为[I′k]，B所在的一端电流为[I″k]，流经过渡阻抗[Rg]的电流为[Ik=I′k+I″k]，此时保护1和2的测量阻抗分别简化为：

[Zk.1=UAI′k=Ik·Rg·ejθI′k+ZAB=ZAB+Rg+I″kI′k·Rg·ejθ1]      （3）

[Zk.2=UBI′k=Ik·Rg·ejθI′k]                            （4）

式中，[θ]表示[I′k]超前[I″k]的角度[8]。保护1的测量阻抗含有[I″kI′k·Rg·ejθ1]的分量，根据角度的不同阻抗的性质也会发生改变。当保护安装于受电端时，线路中为阻感性，测量值增大到一定值时，极易造成保护内动作;反之，若将保护置于送电端时，线路中呈现容抗的性质。当容抗值不断减小时，会导致保护装置无法精准判定故障位置。

表1比较了过渡电阻对不同电网结构的影响。

5 不同动作特性阻抗继电器的原理分析

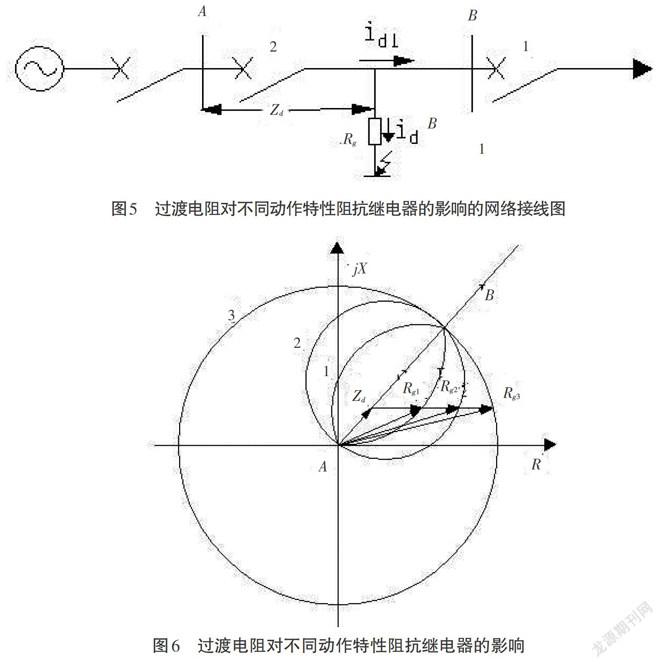
过渡电阻对不同动作特性阻抗继电器的影响的网络接线图见图5;过渡电阻对不同动作特性阻抗继电器的影响见圖6。

从图6可知，当过渡电阻为[Rg1]时，叠加后的阻抗值刚好落在阻抗继电器1的动作边界上，此时阻抗继电器1不动，阻抗继电器2和继电器3会动作。同理，当过渡电阻为[Rg2]时，阻抗继电器1一定不会动作，此时测量阻抗落在阻抗继电器2的边界上，处于临界状态，阻抗继电器2可能不会动作，阻抗继电器3动作。由此可得，应尽可能选择动作特性在横坐标方向上所占面积大的阻抗继电器。

表1 过渡电阻对不同电网结构的影响情况

[影响类别 阻抗的性质 测量阻抗 保护范围 影响情况 单侧电源线路 纯阻性 增大 缩小 保护拒动 双侧电源线路 阻容性 减小 扩大 保护误动 阻感性 增大 缩小 保护拒动或反向出口故障失去方向性 ]

6 四边形特性阻抗继电器的测试分析

在系统实际运行中，多边形继电器在距离保护中使用较为广泛，但一旦出现用于测距功能的元件与横坐标平行，发生超越现象的可能性极大，这也是多边形继电器的弊端。图7为阻抗继电器示意图。四边形特性阻抗继电器各边界的功能见表2。

<F：＼欢欢文件夹＼201904＼河南科技201901＼河南科技（创新驱动）2019年第01期_103595＼Image＼image26.jpeg>[jX][X][A][Y][0][C][β][α][R][R][B]

图7 四边形阻抗继电器特性图

表2 四边形特性阻抗继电器各边界的功能

[保护边界 功能 相应倾角 倾角作用 AB 测距 [δ] 防止超越 BC 躲负荷 [α] 减少末端阻抗值 OB 方向判定 [β] 消除电势差的影响 OA 方向判定 [γ] 防止拒动 ]

从表2可知，AB段用于确定阻抗整定值，送电端经过渡阻抗发生故障时，测量阻抗的电抗值减小，随着线路的逐渐增加，对系统的影响越大，具有一定的倾斜角[δ]可以防止超越带来的影响。为了克服末端受过渡电阻影响较大的问题，BC段的倾斜角设为[α]。当出口处经过渡电阻短路时，两侧线路因为出现电势差影响保护动作，适当调整直线OC段的倾斜角[β]能保证保护可靠动作。当线路发生金属性短路时，由于电压、电流互感器的角度误差，所得测量阻抗的相位可能会超过90°，为了防止拒动，设置OA倾斜角度[γ]。使用时，不断调整好角度，可以有效解决实际线路中的问题。笔者总结了两种现阶段可以运用在电力系统中的方案。

6.1 利用距离保护Ⅲ段特性动作方程

距离保护Ⅰ、Ⅱ、Ⅲ段的动作特性是利用保护整定值的不同来确定发生故障的位置，由于距离的不同，Ⅰ段和Ⅱ段的动作不会影响Ⅲ段的动作情况，所以，可以利用移相法测得距离保护Ⅲ段的动作阻抗值[9]。如四边形特征图（见图7）所示，在以R、X的坐标平面内设置X点的阻抗值为[xm]。

其中，AB边界倾斜角为[k1]，对应AB边界方程为：

[XAB+k1·R=xm]                             （5）

BC边界的倾斜角度为[k2]，相应的倾斜角为[α]，得[k2=tanα]，对应BC边界方程为：

[XBC=k2·R-Rm]                        （6）

OC边界的倾斜角度为[k3]，相应的倾斜角为[β]，得[k3=tanβ]，对应OC边界方程为：

[XOC=R·tanβ]                             （7）

OA边界边界方程为：

[XOA=R·tanδ]                            （8）

根据四边形特性的边界条件，利用移相法，调整功角范围[β～γ]，更换极坐标，设置移相角为[θ]，在稳定电流值I的基础上，调节电压值U，减少电压值到形成一条以过原点的一次函数直线，移相角[θ]与直线之间的方程为：

[X=R·tanθ]                                （9）

边界线AB边界设置一点[Z1]，联立方程（5）和（9）可得：

[Z1∠θ1=R1+jX1]                         （10）

[R1=Xmk1+tanθ1]                             （11）

[X1=Xmk1+tanθ1·tanθ1]                         （12）

[Z1=R21+X21=Xmk1cosθ1+sinθ1]             （13）

對应B点处的功角为[θB]，[Z1]的功角范围应在[θB～γ]变化，其角度为：

[θB=tan-1XBRB]                                    （14）

同理，在边界线BC边界设置一点Z2，联立方程（5）和（9）可得：

[Z2∠θ2=R2+jX2]                        （15）

[R2=k2k2-tanθ2·R]                         （16）

[X2=k2k2-tanθ2·R·tanθ2=k2·R2-Rm]     （17）

[Z1=k2k2cosθ2-sinθ2·R]                     （18）

[Z1]的功角范围应在[β～θB]变化。

设定距离保护中Ⅰ、Ⅱ、Ⅲ的整定时间为[t1]、[t2]和[t3]时满足：

[t3=t2+Δt=t1+Δt+Δt]                            （19）

设置电压值的跳变时间为：

[tb=t2+t33]          &nbsp;                           （20）

6.2 四边形动作特性阻抗继电器的改进方案

6.2.1 圆弧边界法。四边形特性继电器的边界区，其规律特性与距离保护Ⅲ段的特性不同，同一阻抗角对应多种阻抗值，无法用常规方案解决问题，现采用圆形边界法改变相位的方式来测试边界的动作阻抗，设定阻抗角为[ϕ]，角度所对应的阻抗值为[ZC]，选取OC的长度作为圆弧半径，分别取OC的长度0.1、0.3、0.5、0.7、0.9和1倍等8个数据，以坐标原点为圆心，角度在原阻抗角[ϕ]上[±8°]，步长设定为1°，不断调整圆心角，确定OC边界的动作阻抗值。同理，设定OA边界的阻抗角，设定圆弧范围，收集数据。

6.2.2 电压跳变法。采用距离保护时，Ⅲ段保护不受Ⅰ、Ⅱ段工作情况的影响，利用电压、电流关系确定动作阻抗，以保护边界AB上一点Q作为整定计算值点，确定相角为[θ3]，联立方程（5）和（13）可得Q点处的电压值与电流值。调整初始状态Ⅲ段保护Q点处的电压值为[UQ]，选取0.8V作为步长，设定电压的变化量以0.8V步长逐次递减，确定继电器发生动作时动作阻抗的大小。若在保护区外，则改变电压大小，直到达到满足Ⅱ段保护动作范围。每调节一次电压跳变值，以步长8°为单位改变，每次跳变，一旦无法进入保护Ⅱ段范围，电压值将跳变为该次电压值与上一次跳变值之和的平均值，以次类推直到落入规定范围，获取精确的电压值。随后，利用公式（13）获取各段阻抗值，从而确定边界的精确范围。

表3 边界阻抗值的测试结果

[角度/° 阻抗值/Ω -10 3.37 -10 5.89 -10 9.16 -10 13.44 125 3.98 125 10.07 125 16.24 125 28.75 ]

表4 实验中三段保护的测量阻抗值

[角度/° Ⅰ段阻抗值/Ω Ⅱ段阻抗值/Ω Ⅲ段阻抗值/Ω 0 11.91 10.88 7.27 5 12.57 11.38 9.31 10 13.12 11.98 12.08 15 11.07 10.79 13.21 20 8.45 10.01 14.16 25 7.58 10.22 16.01 30 6.13 10.46 17.45 35 14.33 16.89 18.64 40 20.92 19.14 19.22 45 4.03 8.02 25.63 50 3.82 7.51 30.24 55 3.66 7.09 33.99 60 3.41 6.53 37.71 65 3.28 6.31 34.16 70 3.03 5.86 30.97 75 2.97 5.64 30.08 80 2.91 5.55 29.34 85 2.89 5.46 29.01 90 2.87 5.45 28.75 95 2.87 5.45 30.45 100 2.87 5.45 32.21 105 2.88 5.51 31.44 ]

6.2.3 数据分析。以本文提及的四边形特性阻抗继电器為实例进行实验测试，设定动作边界为-15°～125°（通常情况下取值为105°～120°），阻抗角[ϕ]的范围为0°～105°，使用跳变电压时取步长为8°，测得阻抗值大小。再利用三段式距离保护保护范围及其动作特性确定在不同阻抗角的设定下的阻抗值。边界阻抗值的测试结果见表3。实验中三段保护的测量阻抗值见表4。

实验结果表明，数据的精确度越高，与四边形特性的阻抗继电器的理想图形越近似。由上述数据确定的四边形边界与理想情况下的图像偏差小，基本符合系统运行要求。

7 结语

通过采用动作边界的特性来改变电压值和阻抗角度的方案，确定线路故障的具体位置，解决四边形特性继电器使用上的缺陷，极大提高了运行时阻抗测量值的精确程度。随着技术逐渐成熟，有望不断完善距离保护中有关测量阻抗的精确度问题，有利于消除过渡电阻的影响，保证电网运行的安全性和可靠性。

参考文献：

[1]张晶晶，曹锐.距离保护特性元件躲过渡电阻能力分析与研究[J].继电器，2004（6）：17-19.

[2]黄少锋，曹凯，罗澜.一种消除过渡电阻影响的阻抗测量方法[J].电力系统自动化，2013（23）：108-113.

[3]黄少锋，江清楷.过渡电阻对多相补偿阻抗元件影响的分析及对策[J].电网技术，2011（8）：202-206.

[4]沈冰，何奔腾.基于阻抗轨迹估计的自适应相间距离继电器[J].中国电机工程学报，2007（31）：71-76

[5]连晶晶，赵志英.四边形特性阻抗继电器探讨[J].南昌工程学院学报，1997（1）：53-56.

[6]马伟，丁东，裘愉涛，等.提升距离保护抗过渡电阻能力的研究综述[J].电力系统保护与控制，2019（1）：166-176.

[7]王怡君.人工神经网络在距离继电器保护中的应用研究[D].北京：华北电力大学，2015.

[8]许建安.电力系统继电保护[M].北京：中国水利水电出版社，2004.

[9]邰彬，文劲宇，王李东.四边形特性阻抗继电器动作边界测试方法的研究[C]//中国高等学校电力系统及其自动化专业学术年会.2004.