化归思想在锐角三角函数中的巧用

董美程

化归思想就是将面临的新问题转化为已经熟悉的规范问题的数学方法。后者具有确定的解法或有确定的求解程序。这是一种具有普遍适用性的数学思想方法。一般总是将复杂问题通过变换转化为简单问题，将难解的问题通过变换转化为容易求解的问题，将未解决的问题通过变换转化为已解决的问题。

化归包含三个要素：①化归动象（我们不熟悉的新问题图）②化归的目标（规范问题图）：③化归的途径。下面将化归思想在锐角三角函数这章的渗透列举一二。

锐角三角函数体现的是直角三角形中边和角的关系，若求某个锐角的三角函数值或要运用某个锐角的三角的数值求线段的长度，而这个锐角不在直角形中时，则必须通过转化的思想化斜为直，其化归的途径主要有两种：

（1）直接求：构造直角三角形，把这个角放在直角三角形里。

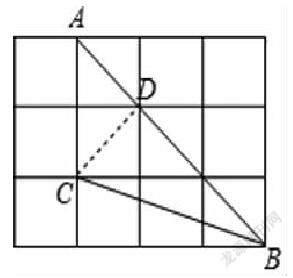
例1.如图，在边长相同的小正方形组成的网格中，点、、都在这些小正方形的顶点上，则tan∠的值为.

点拨：连接根据勾股定理的逆定理，可证△CDB为直角三角形。则把∠ABC放在了直角三角形里，即可求∠ABC的正切值。

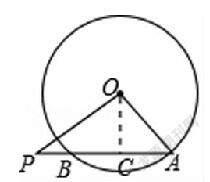
例2.如图，⊙的半径为5，弦的长为8，是延长线上一点，=2，则tan∠的值是 .

点拨：过点O做AP的垂线，垂足为C，则将∠P放在了Rt△OCP里。利用垂径定理即可解决问题。

（2）间接求：转化为與之相等的角。

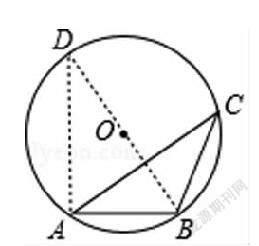
例3.如图，在半径为13的⊙中，弦=10，点是优弧上一点（不与，重合），则cos的值为 .

点拨：作直径，连接，根据圆周角定理得出∠=∠，∠=90°，根据勾股定理求出，解直角三角形求出即可.

总之，化归在数学解题中几乎无处不在。著名数学家笛卡尔说过“我一生只做两件事情，一是做简单的事情，二是将复杂的事变成简单的事。”第二句话实质上运用了化归的思想。